Matemática pode ser uma verdadeira dor de cabeça, e eu não estou falando do tipo simples x + y. Adicione algumas estruturas financeiras DeFi na equação, e você está preparado para um mundo de problemas. Não só você precisa decifrar fórmulas complexas, como também precisa ficar por dentro do mundo em constante evolução da DeFi (incluindo todo o jargão!). É como o Brooklyn – você tem que ficar alerta e ágil ou corre o risco de ser pego de surpresa. Como sua mercearia de confiança fechando de repente. Um dia está lá, no dia seguinte... poof!
Entender o Uniswap não é diferente. Se você acha que entendeu o Constant Function Market Maker (CFMM ou formador de mercado de função constante) do Uniswap V2, espere até mergulhar no Uniswap V3. Com a introdução da liquidez concentrada, você precisará repensar seu entendimento de como o Uniswap funciona quando aplicá-lo praticamente ao código.
O que abordaremos
- Revisão da Matemática do Uniswap V2
- Foco na Matemática de Swap do Uniswap V3
- Como aplicar a matemática de negociação do V3 ao código dinâmico
Pré-requisitos
- Entendimento básico de pools de liquidez (se não tiver, nós te ajudamos)
- Habilidades matemáticas médias
- Este artigo servirá como uma extensão mais aprofundada de nossos artigos anteriores. Ele fornecerá uma visão mais profunda de como a matemática funciona com o código.*
pools de liquidez
Um pool de liquidez é um contrato inteligente que contém um conjunto de tokens usados para negociação em exchanges descentralizadas (DeXs). Nas DeXs, compradores e vendedores negociam diretamente uns com os outros e o pool de liquidez atua como facilitador dessas negociações.
Quando um usuário inicia uma negociação, o pool de liquidez executa automaticamente a negociação usando um algoritmo que equilibra as proporções de tokens no pool. O preço da negociação é determinado pela proporção de tokens no pool e pelo tamanho da negociação.
À medida que mais usuários adicionam tokens ao pool de liquidez, a profundidade do pool aumenta, tornando-o mais atraente para os negociadores. Isso cria um ciclo autorreforçado onde a profundidade do pool atrai mais negociadores, levando à geração de mais taxas para os provedores de liquidez.
I. Uniswap V2: Uma revisão sucinta
O Uniswap V2 em sua essência é um market maker (formador de mercado) automatizado (AMM), que é uma exchange descentralizada que se baseia em fórmulas matemáticas para determinar o preço dos ativos com base em sua oferta e demanda. Isso permite a negociação ponto a ponto (peer-to-peer) sem a necessidade de um intermediário, como RobinHood, TD Ameritrade ou Coinbase.
Como um AMM, a fórmula matemática que o V2 implementa é chamada de CPMM (market maker de produto constante).
Como uma fórmula básica:
Vamos desmembrar isso – o conceito-chave por trás das operações do Uniswap é que o produto das reservas de tokens permanece constante antes, durante e após uma negociação. Essencialmente, os negociadores podem trocar um token por outro, mas o valor total das reservas permanece o mesmo. Esta é a fórmula central que alimenta todo o protocolo do Uniswap.
Mas é aqui que fica interessante: usando este simples princípio, podemos descobrir os preços de tokens individuais e até mesmo criar uma fórmula de negociação para determinar nossos retornos. Por exemplo, se entendemos que o produto das reservas deve permanecer consistente, podemos calcular o preço à vista de um token em relação ao seu par.
Os preços dos tokens em um pool são determinados pela oferta de tokens disponíveis, que é baseada nas reservas detidas pelo pool. E adivinhe? Os preços dos tokens são apenas proporções dessas reservas! Peguemos o exemplo de um pool MATIC/USDC. Se o pool tem 5.000 MATIC e 10.000 USDC, então 1 MATIC valeria 0,5 USDC, enquanto 1 USDC valeria 2 MATIC. Até agora, tudo bem, certo?
Como descobrimos quanto de cada token receberemos em uma negociação? Digamos que queremos trocar algum MATIC por USDC. Podemos usar uma pequena função útil que trabalha com o mesmo pool MATIC/USDC que acabamos de mencionar.
- R1 são as reservas de MATIC 5.000
- R2 são as reservas de USDC 10.000
- Δa é a quantidade de MATIC que estamos vendendo
- Δb é a quantidade de USDC que receberemos
- r é denotado como 1 – r e representa nossa taxa (em relação ao Uniswap V2, é uma taxa fixa de 3%)
Usando manipulação algébrica básica, podemos facilmente encontrar a quantidade de MATIC (Δa) ou USDC (Δb).
Eu sei que toda essa conversa sobre fórmulas, reservas e negociação pode parecer muita informação. Mas aqui está o ponto: se você quiser colocar isso em código, é realmente muito simples. Tudo o que você precisa é de uma função que possa trocar as variáveis dependendo se você está comprando ou vendendo tokens. Mantenha simples, estúpido - esse é o princípio KISS (Keep It Simple, Stupid)!
function uniswap_V2_Math_swap(pool, token_in, token_out, amount) {
const token_in_reserves =
token_in === pool.token0.id
? Number(pool.reserve0)
: Number(pool.reserve1);
const token_out_reserves =
token_out === pool.token0.id
? Number(pool.reserve0)
: Number(pool.reserve1);
const calculated_amount = Math.abs(
(token_in_reserves * token_out_reserves) / (token_in_reserves + amount) -
token_out_reserves
);
return calculated_amount;
}
Vamos apimentar esta fórmula com um exemplo prático e alguns gráficos legais! Não se preocupe, eles estão aqui apenas para nos ajudar a entender os prós e contras do sistema (CPMM) do Uniswap. Confie em nós, até o final, você entenderá.
Como a liquidez de um pool é distribuída uniformemente ao longo da curva de preço de 0 a infinito. Isso garante que sempre haverá liquidez disponível para ser negociada, no entanto, os preços, é claro, mudarão em relação à quantidade de reservas no pool.
Vamos utilizar nossa fórmula de negociação e observar a reação da curva de preço. Supondo que pretendemos negociar 1.000 MATIC por USDC dentro do pool de liquidez MATIC/USDC, onde as reservas de MATIC estão em 5.000 e as reservas de USDC em 10.000.
Os eixos USDC e MATIC representam as reservas dos dois tokens. O processo de negociação começa no "valor k atual" e sobe à medida que mais MATIC é adicionado e USDC é removido, resultando em um novo ponto de partida para a próxima troca, enquanto ainda adere aos princípios fundamentais da função CPMM.
Pronto! Chegamos ao fim! Embora ainda haja muito mais que podemos cobrir, como matemática na provisão de liquidez e lidar com a derrapagem (slippage), confira nossos pontos de referência abaixo. Mas por enquanto, vamos nos ater ao emocionante mundo dos cálculos de negociação. Embora tenhamos coberto muito terreno, como eles se comparam ao Uniswap V3? E o que faz esta última versão se destacar da V2?
II. Uniswap V3: Matemática de Swap
O princípio chave do Uniswap V3 é a liquidez concentrada, o que significa que a liquidez é focada em uma faixa de preço específica, em vez de distribuída uniformemente ao longo da curva de preço como era no V2. Esta abordagem melhora a eficiência de capital ao permitir que mais liquidez seja alocada numa faixa de preço menor. Assim, resultando em pools de liquidez adaptados a pares com diferentes níveis de volatilidade.
No V3, a liquidez é fragmentada em pares ao longo da curva de preço, cada um com uma quantidade finita de liquidez. Conforme a liquidez se esgota em um par, o protocolo muda para o próximo par dentro da mesma faixa de preço. Embora o processo de alocação de liquidez em intervalos seja diferente do Uniswap V2, a matemática que sustenta o protocolo permanece fundamentalmente a mesma.
Embora o V3 compartilhe as mesmas fórmulas básicas do V2, incorpora melhorias significativas que aprimoram sua eficiência e funcionalidade. Para obter maior precisão nos cálculos, o Uniswap V3 emprega a formatação Q64.96 e introduz novos conceitos.
Então, quando um par dentro do intervalo fica sem liquidez, como o pool se move para o próximo par?
Suponha que tenhamos um par dentro do intervalo (WETH/USDC) representado no gráfico acima. Para passar para o próximo intervalo, precisamos trocar todas as reservas restantes de WETH (token 1) por USDC (token 0) dentro desta faixa de preço. Isso faria nossa curva atual desaparecer, e a precificação do pool de liquidez "escorregaria" para a próxima faixa de preço onde ambos os ativos têm liquidez.
Vamos explorar mais examinando os seguintes dados do pool de liquidez de um par WETH/USDC.
A liquidez no pool é representada por L e é derivada do produto das reservas de token, denotadas como x e y, que é uma constante k. A medida da liquidez é calculada como a raiz quadrada de x vezes y. Esse valor pode ser multiplicado por ele mesmo para obter k.
Ao calcular a raiz quadrada do preço (√P) de cada token. O preço de WETH em termos de USDC é y/ x. Enquanto os preços em um pool de liquidez são recíprocos uns dos outros, o preço do USDC em termos de WETH é, de forma semelhante, x/ y.
Pode-se inferir que há uma correlação entre a liquidez e a precificação, já que o V3 fragmenta a liquidez em várias faixas de preço. Essencialmente, a liquidez e o √P inicial podem ser descritos como a associação entre a mudança na quantidade de saída (y || x) e a mudança no √P. A partir disso, obtemos:
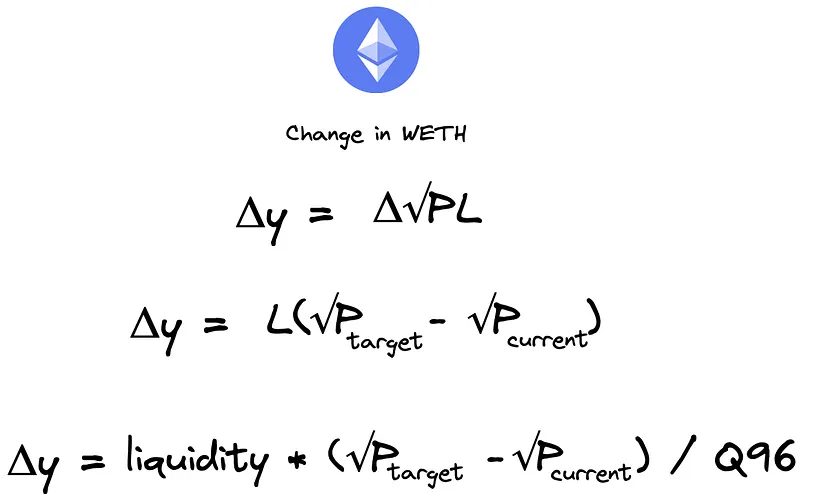
Usando esta fórmula, podemos inserir os valores e aplicar manipulação algébrica para obter uma fórmula para a mudança no token 0 (y) e a mudança no token 1 (x). *O Token 1 é encontrado no conhecimento de que as precificações de tokens são recíprocas umas das outras.
A ideia principal aqui é descobrir a variação na raiz quadrada do preço (Δ√P). Ao determinar Δ√P, podemos não apenas identificar o estado do pool posteriormente, mas também calcular a quantidade resultante de um token que obteremos. Para conseguir isso, podemos desenvolver fórmulas distintas para cada um.
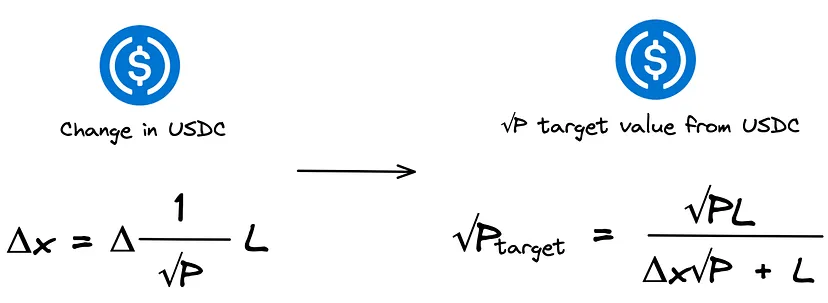
Assumindo uma negociação de 0.05 WETH por USDC em nosso pool USDC(x)/WETH(y), só precisamos da raiz quadrada do preço (√P) e da liquidez (L). A partir disso, podemos usar nossa fórmula existente para WETH e convertê-la para determinar Δ√P. Simplesmente, inserimos os valores de Δy (quantidade de WETH) e L (a liquidez de nossos dados).
Com o valor da mudança na raiz quadrada do preço (Δ√P), podemos calcular nosso preço alvo. Uma vez que conhecemos o preço alvo, nossa fórmula pode usar esse resultado para calcular quantos tokens de saída nosso input nos fornecerá.
Em seguida, obtemos nossa fórmula para inserir nosso atual √P e nosso √P alvo. Tomando a fórmula de mudança no USDC, expandimos e alteramos para obter nossa fórmula para calcular a quantidade de USDC.
Usando essa fórmula, inserimos os valores que temos de nosso conjunto de dados (liquidez e sqrtPrice atual). Também inserimos o valor alvo que encontramos a partir da quebra na mudança de WETH.
Para calcular a quantidade de tokens que receberemos de uma negociação V3, precisamos apenas do sqrtPrice atual e da liquidez. Usando esses valores, podemos determinar o sqrtPrice alvo, considerando a quantidade de nossa entrada e a liquidez atual do pool. Uma vez que temos o sqrtPrice alvo, podemos aplicar nossa fórmula de saída, com base na posição do token (token 0 ou token 1), e resolver a quantidade de saída usando manipulação algébrica simples.
III. V3_Math_to_Code
Vamos pegar os seguintes dados de um pool de liquidez USDC/WETH. Usando esses dados como ponto de partida, seguiremos explicando como calculamos a quantidade resultante de uma swap. *Estaremos seguindo a divisão que estabelecemos na seção anterior (ou seja, negociando WETH por USDC) com nossos dados de entrada.
//------ data queired from The Graph -------//
{
id: '0x88e6a0c2ddd26feeb64f039a2c41296fcb3f5640',
token0Price: '1686.164670626403779210062751107168',
token1Price: '0.0005930618861967400806594493909084589',
liquidity: '51568192164898145374',
sqrtPrice: '1929432505955379480598923934630247',
token0: {
symbol: 'USDC',
decimals: '6',
id: '0xa0b86991c6218b36c1d19d4a2e9eb0ce3606eb48',
derivedETH: '0.0005944169825801652979776390737364143',
price: '1686.164670626403779210062751107168'
},
token1: {
symbol: 'WETH',
decimals: '18',
id: '0xc02aaa39b223fe8d0a0e5c4f27ead9083c756cc2',
derivedETH: '1',
price: '0.0005930618861967400806594493909084589'
},
reserve0: '2117454393.78841',
reserve1: '12.14095',
exchange: 'uniswapV3',
fee: '500',
token_in: '0xc02aaa39b223fe8d0a0e5c4f27ead9083c756cc2',
token_out: '0xa0b86991c6218b36c1d19d4a2e9eb0ce3606eb48'
}
Como mencionado, o Uniswap usa um formato de número Q64.96 para armazenar o valor de P. Este formato é um número de ponto fixo com 64 bits para a parte inteira e 96 bits para a parte fracionária. Portanto, é importante para nós, converter nossas entradas para um formato Q64.96. Felizmente, essa conversão é direta - só precisamos multiplicar os números decimais pela base do Q64.96, que é 2⁹⁶. Assim, na construção de nossa função, devemos rotular de forma clara e precisa nossas variáveis convertidas neste formato.
**Uniswap usa o formato de número Q64.96 para armazenar preços porque ele fornece um alto nível de precisão com requisitos mínimos de armazenamento, tornando-o uma escolha eficiente para a plataforma.
function uniswap_V3_swap_math(pool, amount) {
// usado para determinar qual posição de token estamos negociando
const token_0_is_token_in = pool.token_in === pool.token0.id;
// conversão q96
const q96 = 2 ** 96;
// os decimais do token também são convertidos para
// converter com precisão a entrada e os valores resultantes
const token_0_decimals = 10 ** Number(pool.token0.decimals);
const token_1_decimals = 10 ** Number(pool.token1.decimals);
// convertendo strings para números
const liquidity = Number(pool.liquidity);
const current_sqrt_price = Number(pool.sqrtPrice);
}
Uma vez que as variáveis estão configuradas, podemos prosseguir adicionando declarações condicionais para lidar com as fórmulas com base na posição do token de entrada. Essas declarações condicionais nos ajudarão a determinar o √P alvo, que é a etapa inicial em nosso processo matemático.
function uniswap_V3_swap_math(pool, amount) {
const token_0_is_token_in = pool.token_in === pool.token0.id;
const q96 = 2 ** 96;
const token_0_decimals = 10 ** Number(pool.token0.decimals);
const token_1_decimals = 10 ** Number(pool.token1.decimals);
const liquidity = Number(pool.liquidity);
const current_sqrt_price = Number(pool.sqrtPrice);
if(!token_0_is_token_in) {
/// converter nosso valor em conta para os decimais que ele usa
const amount_in = amount * token_1_decimals;
const price_diff = (amount_in * q96) / liquidity; // === (Δ√P)
const price_target_value = price_diff + current_sqrt_price // === √P target value
}
}
Agora que temos nosso √P alvo, aplicamos nosso método para encontrar a saída de tokens USDC. O valor retornado terá que ser convertido em seu ponto decimal apropriado (USDC é 6, WETH é 18). Curioso sobre pontos decimais em criptomoedas? — decimais explicados.
function uniswap_V3_swap_math(pool, amount) {
const token_0_is_token_in = pool.token_in === pool.token0.id;
const q96 = 2 ** 96;
const token_0_decimals = 10 ** Number(pool.token0.decimals);
const token_1_decimals = 10 ** Number(pool.token1.decimals);
const liquidity = Number(pool.liquidity);
const current_sqrt_price = Number(pool.sqrtPrice);
function calc_amount0(liquidity, price_target_value, current_sqrt_price) {
if (price_target_value > current_sqrt_price) {
[price_target_value, current_sqrt_price] = [
current_sqrt_price,
price_target_value,
];
}
return Number(
(liquidity * q96 * (current_sqrt_price - price_target_value)) /
current_sqrt_price /
price_target_value
);
}
if (!token_0_is_token_in) {
/// converter nosso valor em conta para os decimais que ele usa
const amount_in = amount * token_1_decimals;
const price_diff = (amount_in * q96) / liquidty; // === (Δ√P)
const price_target_value = price_diff + current_sqrt_price; // === √P target value
const output = calc_amount0(
liquidity,
price_target_value,
Number(current_sqrt_price)
);
return output / token_0_decimals;
}
Embora essa função seja projetada principalmente para trabalhar com trocas de tokens do token 1 para o token 0, como podemos construir uma função semelhante para trocas de tokens do token 0 para o token 1?
Podemos manter a estrutura da função atual e modificá-la para funcionar para trocas de tokens do token 0 para o token 1. Ao adicionar à instrução condicional e inserir os mesmos passos de antes, usamos os recíprocos da matemática atual utilizada.
Em vez de usar a fórmula WETH para encontrar nosso valor alvo de √P, usamos a fórmula USDC, já que é nossa entrada. Da mesma forma, em vez de usar a fórmula USDC para calcular a quantidade de tokens, usamos a WETH (porque é o que estamos recebendo em retorno).
Incorporando essa última peça ao estado atual da função uniswap_V3_swap_math() - A construção final da função que temos inclui dois parâmetros - um objeto contendo os mesmos pares chave-valor que nosso exemplo inicial e uma quantidade de entrada para o token que o usuário deseja negociar.
Dependendo da chave/valor no token de entrada (usando um UUID de token) determina a quantidade resultante desta função.
function uniswap_V3_swap_math(pool, amount) {
const token_0_is_token_in = pool.token_in === pool.token0.id;
const q96 = 2 ** 96;
const token_0_decimals = 10 ** Number(pool.token0.decimals);
const token_1_decimals = 10 ** Number(pool.token1.decimals);
const liquidity = Number(pool.liquidity);
const current_sqrt_price = Number(pool.sqrtPrice);
function calc_amount0(liquidity, price_target_value, current_sqrt_price) {
if (price_target_value > current_sqrt_price) {
[price_target_value, current_sqrt_price] = [
current_sqrt_price,
price_target_value,
];
}
return Number(
(liquidity * q96 * (current_sqrt_price - price_target_value)) /
current_sqrt_price /
price_target_value
);
}
function calc_amount1(liquidity, price_target_value, current_sqrt_price) {
if (price_target_value > current_sqrt_price) {
[price_target_value, current_sqrt_price] = [
current_sqrt_price,
price_target_value,
];
}
return Number((liquidity * (current_sqrt_price - price_target_value)) / q96);
}
if (!token_0_is_token_in) {
/// converter nosso valor em conta para os decimais que ele usa
const amount_in = amount * token_1_decimals;
const price_diff = (amount_in * q96) / liquidity; // === (Δ√P)
const price_target_value = price_diff + current_sqrt_price; // === √P target value
const output = calc_amount0(
liquidity,
price_target_value,
Number(current_sqrt_price)
);
return output / token_0_decimals;
} else {
// vendendo token USDC 0 para token WETH 1
const amount_in = amount * token_0_decimals;
const price_target_value =
(liquidty * q96 * current_sqrt_price) /
(liquidty * q96 + amount_in * current_sqrt_price);
const output = calc_amount1(
liquidity,
price_target_value,
Number(current_sqrt_price)
);
return output / token_1_decimals;
}
}
Recursos e Leituras Adicionais
- Uniswap V2 whitepaper
- Uniswap V3 whitepaper
- Build your own Uniswap DeX — Fortemente baseado em matemática
- liquidity pools
Esse artigo é uma tradução feita por @bananlabs. Você pode encontrar o artigo original aqui




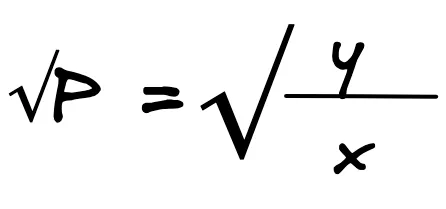







Oldest comments (0)