Da última vez, introduzimos uma implementação ingênua de um verificador em um contrato inteligente Solidity, juntamente com o conceito de insumos públicos e privados.
Nos bastidores do protocolo zkSNARK Groth16 (parte 5)
No entanto, não nos aprofundamos no raciocínio por trás dessa diferenciação. Quando o provador apresenta ao verificador uma prova gerada exclusivamente a partir de dados privados, a prova em si carece de substância suficiente para garantir ao verificador que os dados apropriados foram utilizados. Por exemplo, vamos supor que Alice queira verificar um extrato sobre sua conta bancária usando exatamente esse comprovante. Para o verificador, Bob, a prova pode parecer legítima. No entanto, ele não tem como garantir que a prova não esteja vinculada à conta de outra pessoa. Como tal, a sua declaração deve ser categorizada em dois segmentos: transações públicas e privadas.
- Transações Privadas: São os detalhes confidenciais que Alice opta por não divulgar, como transações menores, como compra de café ou visitas a lojas específicas.
- Transações públicas: abrangem transações maiores e reconhecíveis, como o depósito mensal do salário ou o pagamento de um empréstimo imobiliário.
O objetivo de Alice é afirmar que o saldo de sua conta excede, por exemplo, US$ 10.000, sem expor cada transação individual.
Isto parece razoável. No entanto, para Bob, é crucial ter a certeza de que a opinião pública é genuína e não fabricada. Conseguir isso pode ser extremamente difícil, mas não é impossível. Para resolver isso, o banco (atuando como agente de configuração) fornece dois códigos especiais, γ e δ. Esses códigos aumentam as transações públicas e privadas, mas não fornecem nenhuma pista discernível nem para Bob nem para Alice. Esses códigos de validação garantem a integridade das transações públicas.
γ e δ
Já identificamos que a configuração confiável deve ser estendida com esses dois parâmetros. Também identificamos que estes têm que interagir com insumos públicos e privados.
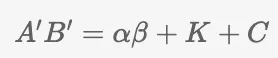
K - público, C - privado
Felizmente para nós, isso significa que precisamos alterar apenas os termos da equação (K e C).
Vamos verificar primeiro usando polinômios:
print("Setup phase")
print("-"*10)
print("Toxic waste:")
alpha = FP(2)
beta = FP(3)
gamma = FP(4)
delta = FP(5)
tau = FP(20)
print(f"α = {alpha}")
print(f"β = {beta}")
print(f"γ = {gamma}")
print(f"δ = {delta}")
print(f"τ = {tau}")
def split_poly(poly):
coef = [int(c) for c in poly.coefficients()]
p1 = coef[-2:]
p2 = coef[:-2] + [0] * 2
return galois.Poly(p1, field=FP), galois.Poly(p2, field=FP)
u = U(tau)
v = V(tau)
ht = H(tau)*T_tau
U1, U2 = split_poly(U)
V1, V2 = split_poly(V)
W1, W2 = split_poly(W)
w1 = W1(tau)
w2 = W2(tau)
u1 = U1(tau)
u2 = U2(tau)
v1 = V1(tau)
v2 = V2(tau)
c = (beta * u2 + alpha * v2 + w2) * delta**-1 + ht * delta**-1
k = (beta * u1 + alpha * v1 + w1) * gamma**-1
a = u + alpha
b = v + beta
assert a * b == alpha * beta + k * gamma + c * delta # deve ser igual.
O que fizemos aqui foi apenas dividir os dois termos por gama e delta:
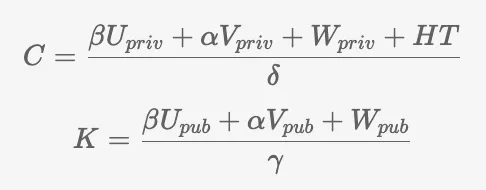
Durante a etapa de verificação, K e C são multiplicados por esses valores, o que os cancelará e deixará a equação inicial intacta. Claramente,γ e δ devem ser fornecidos ao verificador de forma criptografada, especificamente como pontos de curva elíptica.
Configuração confiável:
print("Fase de configuração")
print("-"*10)
print("Lixo tóximo:")
alpha = FP(2)
beta = FP(3)
gamma = FP(4)
delta = FP(5)
tau = FP(20)
print(f"α = {alpha}")
print(f"β = {beta}")
print(f"γ = {gamma}")
print(f"δ = {delta}")
print(f"τ = {tau}")
tau_G1 = [multiply(G1, int(tau**i)) for i in range(0, T.degree)]
tau_G2 = [multiply(G2, int(tau**i)) for i in range(0, T.degree)]
powers_tauTtau_div_delta = [(tau**i * T_tau) / delta for i in range(0, T.degree - 1)]
target_G1 = [multiply(G1, int(pTd)) for pTd in powers_tauTtau_div_delta]
assert len(target_G1) == len(H.coefficients()), f"target_G1 length mismatch! {len(target_G1)} != {len(H.coefficients())}"
K_gamma, K_delta = [k/gamma for k in K_eval[:2]], [k/delta for k in K_eval[2:]]
K_gamma_G1 = [multiply(G1, int(k)) for k in K_gamma]
K_delta_G1 = [multiply(G1, int(k)) for k in K_delta]
print("Configuração confiável:")
print("-"*10)
print(f"[α]G1 = {normalize(alpha_G1)}")
print(f"[β]G2 = {normalize(beta_G2)}")
print(f"[γ]G2 = {normalize(gamma_G2)}")
print(f"[δ]G2 = {normalize(delta_G2)}")
print(f"[τ]G1 = {[normalize(point) for point in tau_G1]}")
print(f"[τ]G2 = {[normalize(point) for point in tau_G2]}")
print(f"[τT(τ)/δ]G1 = {[normalize(point) for point in target_G1]}")
print(f"[K/γ]G1 = {[normalize(point) for point in K_gamma_G1]}")
print(f"[K/δ]G1 = {[normalize(point) for point in K_delta_G1]}")
Fase de configuração
----------
Lixo tóxico:
α = 2
β = 3
γ = 4
d = 5
t = 20
Configuração confiável:
----------
[a]G1 = (1368015179489954701390400359078579693043519447331113978918064868415326638035, 991811005130217158508040260331970277456 5515993150576347155970296011118125764)
[b]G2 = ((2725019753478801796453339367788033689375851816420509565303521482350756874229, 72731651027999311171587147155037790973 5733521218303035754523677688038059653). 2 4722006818841961785324909313781880061366718538693995380805373202866))
[c]G2 = ((18936818173480011669507163011118288089468827259971823710084038754632518263340, 1855614758675378963467077821222448114 46 (448229326945855846642767021074501673839)
[δ]G2 = ((20954117799226682825035885491234530437475518021362091509513177301640194298072, 454044468114725346778530794253022336 45 30218361853237193970751657229138047649), (21508930868448350162258892668132814424284302804699005394342512102884055673846, 116 318 39690097995216017572651900167465857396346217730511548857041925508482915))
[τ]G1 = [(1, 2), (18947110137775984544896515092961257947872750783784269176923414004072777296602, 1229208503769329158608364496643 4670280746730626861846747147579999202931064992), (1626219947120579441354494782674593865413210475263758669204832971331159039701 1, 13296900385261935021718889695689394625708483652039722230815936262285054528714), (216036000706896757664384706613459547824193 55 034652174505468210225883925863279, 15787091953565760722773063158476721787069408761080596737736006929439659379800 015254050 70663195453841654293855276471519589821575313643995787424. 3417460412)]
[τ]G2 = [(10857046999023057135944570762232829481370756359578518086990519993285655852781, 115597320329863871079910040213922857 83925812861821192530917403151452391805634). 367875863433681332203403145435568316851327593401208105741076214120093531)), ((658445688651052856222172029662443174632841252415 63 86210384049614268366928061, 13505823173380835868587575884635704883599421098297400455389802021584825778173, (510159176386055 456 9577488373372350852473588323930260132008193335489992486594, 1753783709436247797639692717863616216761517329092736300374379 4104 386247847571)), ((15315709620702712460485525966545043944570955016708868204420815750896718746085, 8198197634290639555322052 407476 232699891641457211856758911101094525731144652), (19804470431547976995467325770475378164766256111835164108366808772087600 898145, 4235451872741546336515947567132583436895052948569531554551940659752625222062) ) 15592044 28094 304399156219358984665346302412186219957044834017722538687643212)), ((7438610750340884426463248775247096468124645443296586 8797796 3153953325237344, 5808982581765237968275179275525571115489463112173520579009942912940231914163), (125753263562720009516) 45854762 614021668091710139241570303614619233551006506090, 600987892185797510428623699096699739721974087077140569734740259387 2065076583))]
[τT(τ)/δ]G1 = [(10532222137368394818613099059613463160899386378020768122117790269127160784667, 106047931783979576530709060443 0 8503356425743684257720516446506344880506531303), (198248511686712965179287232596041866453554120463763299655697416389734219186 72, 1388142282186114611904832863596419296626407686719457950465320855564914485759), (256943591169803480355632010299391295631280 112 9895388185253163395393665212046, 16962100615446734555007338451722040410800681389299676927599001967306147457509, (647464995 2265) 504125442729327806601139241702920622023685440129133919201199249, 157196639025784732431229423706540083633481965687854664 88603 16291387438243352)]
[K/γ]G1 = [(0, 0), (1540147615742092855122362390273215696202300989980535937807544369063691019287, 91630254088394708046865290486 4832717784863855769927076757632797189693955321)]
[K/δ]G1 = [(16669446524815121333219267530318864581047933015823499703865046203789737572536, 5157664181045350924302328617433280 138295240518266317101128319524740459869530), (11685112056990319855844906381401928404871221435467072756674565751991593098502, 10 24702697817543489078129137147119462713200516932679197626440621457145655412), (4398635625762363462217080872201558840189454499697 030235637073544339893257330, 16796820903752920050374299400542628719635708315959792298511777385609619496404) 39790166407775530733436924511734961303259300200468759582179, 3190141189042914654739402208901291215304387053295982811090075930 029710092020) 339097868431392637030683606434266945717935866), (18574544923839514027016720024936241382974550910907416145411902693712610904236, 16663555989126323052369845513676288824810600544552163110103541438113085430935)]
Provador:
A_G1 = evaluate_poly(U, tau_G1)
A_G1 = add(A_G1, alpha_G1)
B_G2 = evaluate_poly(V, tau_G2)
B_G2 = add(B_G2, beta_G2)
HT_G1 = evaluate_poly(H, target_G1)
# [K/δ*w_priv]G1
Kw_delta_G1_terms = [multiply(point, int(scaler)) for point, scaler in zip(K_delta_G1, w_priv)]
Kw_delta_G1 = Kw_delta_G1_terms[0]
for i in range(1, len(Kw_delta_G1_terms)):
Kw_delta_G1 = add(Kw_delta_G1, Kw_delta_G1_terms[i])
C_G1 = add(Kw_delta_G1, HT_G1)
Prova do provador:
----------
[A]G1 = (1386024683863798223806715768494499062004541323940181712423964207525793364711, 140843658074195725477996606607942635995 385653032596678292076222071924134)
[B]G2 = ((2268131489099612700799057509317325492629365410973939712610009952960246451283, 54602028986188244498510046352089151618 45252587893842541197344609059159079041). 92494964230503385709419527449681227575755609196682056154158621712303733))
[C]G1 = (10674265309145386867701579340117613139347005293915767777967744929866231555068, 21807034771985430326722648124698245516 016073701212659375346472376435314627002)
----------
O verificador usa:
[a]G1 = (1368015179489954701390400359078579693043519447331113978918064868415326638035, 991811005130217158508040260331970277456 5515993150576347155970296011118125764)
[b]G1 = (3353031288059533942658390886683067124040920775575537747144343083137631628272, 193215337665523688609465524374805154414 16830039777911637913418824951667761761)
[k_pub/γ]G1 = [(0, 0), (1540147615742092855122362390273215696202300989980535937807544369063691019287, 91630254088394708046865290486 4 832717784863855769927076757632797189693955321)]
Verificador:
// SPDX-License-Identifier: UNLICENSED
pragma solidity ^0.8.9;
contract PairingTest {
uint256 constant Q =
21888242871839275222246405745257275088696311157297823662689037894645226208583;
struct G1Point {
uint256 x;
uint256 y;
}
struct G2Point {
uint256 x1;
uint256 x2;
uint256 y1;
uint256 y2;
}
struct Proof {
G1Point A;
G2Point B;
G1Point C;
}
struct VerifierKey {
G1Point alpha;
G2Point beta;
G2Point gamma;
G2Point delta;
G1Point IC0;
G1Point IC1;
}
// a prova deve ser fornecida pelo usuário, mas para fins de demonstração nós apenas a codificamos
function proof() public pure returns (Proof memory p) {
p = Proof(
G1Point(1386024683863798223806715768494499062004541323940181712423964207525793364711, 140843658074195725477996606607942635995385653032596678292076222071924134),
G2Point(2268131489099612700799057509317325492629365410973939712610009952960246451283, 5460202898618824449851004635208915161845252587893842541197344609059159079041, 21214978237453897862935673366579439999311734514850735211426933843714547507738, 20956792494964230503385709419527449681227575755609196682056154158621712303733),
G1Point(10674265309145386867701579340117613139347005293915767777967744929866231555068, 21807034771985430326722648124698245516016073701212659375346472376435314627002)
);
}
// o mesmo vale para valores de entrada
function input() public pure returns (uint256[2] memory _input) {
_input[0] = 1;
_input[1] = 104;
}
function verifierKey() public pure returns (VerifierKey memory vk) {
vk = VerifierKey(
G1Point(1368015179489954701390400359078579693043519447331113978918064868415326638035, 9918110051302171585080402603319702774565515993150576347155970296011118125764),
G2Point(2725019753478801796453339367788033689375851816420509565303521482350756874229, 7273165102799931111715871471550377909735733521218303035754523677688038059653, 2512659008974376214222774206987427162027254181373325676825515531566330959255, 957874124722006818841961785324909313781880061366718538693995380805373202866),
G2Point(18936818173480011669507163011118288089468827259971823710084038754632518263340, 18556147586753789634670778212244811446448229326945855846642767021074501673839, 18825831177813899069786213865729385895767511805925522466244528695074736584695, 13775476761357503446238925910346030822904460488609979964814810757616608848118),
G2Point(20954117799226682825035885491234530437475518021362091509513177301640194298072, 4540444681147253467785307942530223364530218361853237193970751657229138047649, 21508930868448350162258892668132814424284302804699005394342512102884055673846, 11631839690097995216017572651900167465857396346217730511548857041925508482915),
G1Point(0, 0),
G1Point(1540147615742092855122362390273215696202300989980535937807544369063691019287, 916302540883947080468652904864832717784863855769927076757632797189693955321)
);
}
function add(
G1Point memory p1,
G1Point memory p2
) public view returns (G1Point memory r) {
(bool ok, bytes memory result) = address(6).staticcall(
abi.encode(p1.x, p1.y, p2.x, p2.y)
);
require(ok, "g1add falhou");
(uint256 x, uint256 y) = abi.decode(result, (uint256, uint256));
r = G1Point(x, y);
}
function mul(
G1Point memory p,
uint256 scalar
) public view returns (G1Point memory r) {
(bool ok, bytes memory result) = address(7).staticcall(
abi.encode(p.x, p.y, scalar)
);
require(ok, "g1mul failed");
(uint256 x, uint256 y) = abi.decode(result, (uint256, uint256));
r = G1Point(x, y);
}
function negate(G1Point memory p) internal pure returns (G1Point memory) {
// The prime q in the base field F_q for G1
if (p.x == 0 && p.y == 0) return G1Point(0, 0);
return G1Point(p.x, Q - (p.y % Q));
}
function run(bytes memory _input) public view returns (bool) {
// opcional, a pré-compilação também verifica isso e reverte (sem erro) se for falso, isso ajuda a restringir possíveis erros
if (_input.length % 192 != 0) revert("Points must be a multiple of 6");
(bool success, bytes memory data) = address(0x08).staticcall(_input);
if (success) return abi.decode(data, (bool));
revert("Emparelhamento errado");
}
function emulate() public view returns(bool) {
return verify(proof().A, proof().B, proof().C, input());
}
function verify(G1Point memory A, G2Point memory B, G1Point memory C, uint256[2] memory _input) public view returns (bool) {
G1Point memory k1 = mul(verifierKey().IC0, _input[0]);
G1Point memory k2 = mul(verifierKey().IC1, _input[1]);
G1Point memory K = add(k1, k2);
// -A * B + alpha * beta + C * delta + K * gamma = 0
bytes memory points1 = abi.encode(
A.x,
negate(A).y,
B.x2,
B.x1,
B.y2,
B.y1,
verifierKey().alpha.x,
verifierKey().alpha.y,
verifierKey().beta.x2,
verifierKey().beta.x1,
verifierKey().beta.y2,
verifierKey().beta.y1
);
bytes memory points2 = abi.encode(
C.x,
C.y,
verifierKey().delta.x2,
verifierKey().delta.x1,
verifierKey().delta.y2,
verifierKey().delta.y1,
K.x,
K.y,
verifierKey().gamma.x2,
verifierKey().gamma.x1,
verifierKey().gamma.y2,
verifierKey().gamma.y1
);
bytes memory points = abi.encodePacked(points1, points2);
return run(points);
}
}
r e s
Neste ponto, pode parecer que terminamos, mas há mais. Até agora, nosso foco era garantir que o verificador, Bob, não fosse enganado pelo provador. No entanto, agora é hora de considerar a perspectiva do provador, neste caso a de Alice. Como o processo de verificação ocorre em um espaço público e inseguro, existe o risco de um impostor pegar a prova e a opinião pública de Alice e usá-la indevidamente para seus próprios fins. Para mitigar isso, o provador deve introduzir aleatoriedade durante a geração da prova. Isso garante que cada prova gerada seja única, mesmo que permaneça válida. Para conseguir isso, o provador deve gerar pontos aleatórios r e s cada vez que o programa de geração de provas é executado. Quanto ao verificador, ele deve acompanhar as provas utilizadas.
A parte do verificador permanece inalterada, implicando que os pontos A, B e C devem ser modificados com os pontos aleatórios r e s. Primeiro, vamos examinar como isso funciona com uma avaliação polinomial não criptografada.
print("Provador escolhe r, s aleatórios")
r = FP(12)
s = FP(13)
print(f"r = {r}")
print(f"s = {s}")
def split_poly(poly):
coef = [int(c) for c in poly.coefficients()]
p1 = coef[-2:]
p2 = coef[:-2] + [0] * 2
return galois.Poly(p1, field=FP), galois.Poly(p2, field=FP)
u = U(tau)
v = V(tau)
ht = H(tau)*T_tau
U1, U2 = split_poly(U)
V1, V2 = split_poly(V)
W1, W2 = split_poly(W)
w1 = W1(tau)
w2 = W2(tau)
u1 = U1(tau)
u2 = U2(tau)
v1 = V1(tau)
v2 = V2(tau)
a = u + alpha + r * delta
b = v + beta + s * delta
c = ((beta * u2 + alpha * v2 + w2) * delta**-1 + ht * delta**-1) + s * a + r * b - r * s * delta
k = (beta * u1 + alpha * v1 + w1) * gamma**-1
assert a * b == alpha * beta + k * gamma + c * delta # deve ser igual
Os parâmetros da configuração confiável são os mesmos, mas a parte dos provadores foi ligeiramente modificada:
r = FP(12) # deve ser aleatório
s = FP(13) # deve ser aleatorio
r_delta_G1 = multiply(delta_G1, int(r))
s_delta_G1 = multiply(delta_G1, int(s))
s_delta_G2 = multiply(delta_G2, int(s))
A_G1 = evaluate_poly(U, tau_G1)
A_G1 = add(A_G1, alpha_G1)
A_G1 = add(A_G1, r_delta_G1)
B_G2 = evaluate_poly(V, tau_G2)
B_G2 = add(B_G2, beta_G2)
B_G2 = add(B_G2, s_delta_G2)
B_G1 = evaluate_poly(V, tau_G1)
B_G1 = add(B_G1, beta_G1)
B_G1 = add(B_G1, s_delta_G1)
As_G1 = multiply(A_G1, int(s))
Br_G1 = multiply(B_G1, int(r))
rs_delta_G1 = multiply(delta_G1, int(-r*s))
C_G1 = add(Kw_delta_G1, HT_G1)
C_G1 = add(C_G1, As_G1)
C_G1 = add(C_G1, Br_G1)
C_G1 = add(C_G1, rs_delta_G1)
print(f"[A]G1 = {normalize(A_G1)}")
print(f"[B]G2 = {normalize(B_G2)}")
print(f"[C]G1 = {normalize(C_G1)}")
[A]G1 = (14614942786781395235323739941473784359708158727987721451462286880826505164913,21619883166399935899647001848432357053098942563907854290524692662449417028110)
[B]G2 = ((319587749637165176148886793271196602371225601986791290743038843027662975010,3799125525057959973194726334738911206921416163026998466480194981504341041059), (14804322218212369892528022736659815952157535301541362469519071425927767448738,15320077395654528648820749046262517324306647091379407731658843025099270151841))
[C]G1 = (17701753435269740403921105970374551089935320911024962898677727136701795584514,14346862312910190547529197118974415823038018600073367279111060787975692996852)
O código do verificador permanece inalterado. No entanto, como estamos codificando A, B e C, implantei o contrato com os parâmetros de entrada finais aqui. Quanto à implementação final do código-fonte que armazenei em um arquivo Python e em um arquivo Jupyter.
Com isso, podemos afirmar com segurança que o protocolo Groth16 está totalmente implementado. Obrigado por ler!
Referências:
- https://www.rareskills.io/post/groth16
- https://eprint.iacr.org/2016/260.pdf
- https://github.com/tornadocash/tornado-core/blob/master/contracts/Verifier.sol#L192
- https://github.com/tarassh/zkSNARK-under-the-hood/blob/main/groth16.ipynb
Este artigo foi escrito por Crypto Fairy e traduzido por Diogo Jorge. O artigo original pode ser encontrado aqui.
