Intro
Seríamos os primeiros a usar aleatoriedade quântica para determinar as características de NFTs?
Nossa entrada no ramo de NFT como desenvolvedores vindo da área de DeFi, abriu portas para possibilidades ainda não exploradas quanto a tecnologias criadoras de destaques na indústria. Cada dia encontramos formas inovadoras e complexas para resolver problemas simples, mas trazendo imensa qualidade no resultado. Primeiramente compreendemos a tecnologia, para então modularizar seu uso em projetos futuros. No artigo em questão, vamos pavimentar o caminho rumo a exploração e implementação da computação quântica para gerar números verdadeiramente randômicos.
O motivo que desencadeou essa pesquisa é o lançamento de um projeto de NFTs. Se você ainda não se aventurou em Tokens, NFTs, Blockchains, mas é um entusiasta da tecnologia, recomendamos que se dedique a conhecer o universo on-chain, fora de corretoras e mídias genéricas.
NFTs são traduzidos para tokens não-fungíveis, significando sua unicidade perante outros tokens. São nativos de blockchains, como Ethereum, Cardano ou Polkadot e são controlados por contratos inteligentes. Sua aparição na mídia teve destaque aos bilhões movimentados em um curto intervalo de tempo, assim como a participação de múltiplas entidades famosas.
Os contratos inteligentes existem dentro de uma abstração acontecendo em tempo real na internet e executam funcionalidades pré-programadas como, por exemplo, criar NFTs. Sendo diversas as possibilidades, algumas se tornaram alvo de tendências, e se tornaram modelos a serem seguidos. Sendo específico em relação a trend, a arte costuma ser uma composição de características, como cabelo, chapéu, óculos, roupa, dentre outros. Esta composição é criada através de código e permite a fusão das diferentes características em uma única obra que será posteriormente vendida como parte de uma coleção online. A maneira como são decididas estas características é puramente pseudo-randômica.
Iremos seguir a mesma ideia de composição que a trend apresenta, no entanto, iremos decidir as características através de números obtidos através de aleatoriedade quântica, ou seja, números verdadeiramente aleatórios (TRNG). E assim garantir que o gerador de artes aleatórias através de composição, garanta a uma verdadeira experiência aleatória. O resultado desse trabalho será a modularização do processo de geração de números aleatórios para uso em projetos futuros. Até então temos mais dois casos de uso, sendo eles, a realização de assinaturas através do método eth_signTypedData (EIP-712), e a atribuição de token URI's contendo IPFS ou metadata relevante para um token específico usando a técnica LazyMint.
Computador Quântico
Essa jornada começou com o projeto de um colega que já vem construindo um grande interesse na área e se dispôs a auxiliar na pesquisa e desenvolvimento. Yan Luis é referência na área de aprendizado e desenvolvimento de smart contracts e fundador da Web3Dev. Sua caminhada resultou na criação da primeira e maior comunidade de desenvolvedores de Web3 no Brasil. Ainda novo, explorou a área de computação quântica e criou conteúdos para auxiliar no entendimento e manuseio de circuitos simulados, assim como configurar o hardware do simulador através do IBM Quantum Experience. Seus projetos podem ser acessados através deste link.
Na computação, quando tratamos de números gerados aleatoriamente, estamos normalmente nos referindo a pseudo-randomismo, cujo resultado aleatório é na verdade um algoritmo determinístico mas que seu resultado é o suficiente para as aplicações que os demandam. Geralmente se usa um modelo de extração de números aleatórios chamado de seed. Esta é geralmente uma pequena string de bits que é utilizada como input para gerar longas sequências de bits seguindo tendências uniformes. Esse processo pode ser modificado para atingir camadas extras de segurança como, por exemplo, o uso de números aleatórios para simulações complexas e precisas envolvendo química orgânica. Ou simples, porém imprescindível, a aleatoriedade para sistemas de loteria. Aos aplicativos que não demandam tanto rigor e possuem um caráter de testes, podem atender ao apelo popular em prol da praticidade e usufruir da alta velocidade de reprodução em relação a outros métodos e também a reprodutibilidade da sequência com foco em teste.
Os números verdadeiramente aleatórios nunca vem do ‘nada’. Eles são definidos como uma série de processos que começam como um evento físico, que é mensurado após a ocorrência, essa medição produz uma sequência de bits que possui um resultado randômico. Este deverá passar por um tratamento de dados, para aumentar sua qualidade e tornar-se o mais uniforme possível.
Algumas aplicações só precisam de algum nível de aleatoriedade, portanto, uma solução simples seria a combinação de duas fontes independentes fracas para produzir um nível mais alto de aleatoriedade verdadeira. O extrator atua como um catalisador que permite encontrar métodos gerais que sempre funcionarão. É basicamente uma matriz aleatória uniforme de bits que são compostos para aumentar a aleatoriedade e existem diferentes algoritmos diferentes para aumentar a eficiência extratora.
Aplicações que demandam um output de natureza aleatória, não devem ser adivinhados, restando recorrer a números verdadeiramente randômicos para manter a seed atualizada e gerar uma cadeia não previsível de números aleatórios. É aqui que entramos no buraco do coelho. O processo de coletar dados completamente imprevisíveis chama-se: coleta de entropia. Estes processos geralmente envolvem a coleta de inputs não previsíveis, sendo padrão algumas técnicas como, o intervalo de acesso ao disco rígido, dados da placa de áudio, movimentação do mouse e pressionamento de teclas. Estes processos citados advém de coleta de processos internos de softwares e podem ser considerados não-determinísticos não-físicos números gerados aleatoriamente (Killmann and Schindler, 2008) que fica em contraste aos números verdadeiramente aleatórios, gerados através de modelos físicos e não determinísticos.
IBM Quantum Experience
Começamos buscando algum ecossistema que pudéssemos ficar imersos em conteúdos sobre computação quântica, foi aí que o Yan apresentou o IBM Quantum Experience. Com uma ótima documentação e uma interface user friendly, disponibiliza ferramentas para criação de circuitos quânticos e também configuração do hardware para execução de testes. Fornecidos pela biblioteca Qiskit, o software de desenvolvimento open-source que opera quantum computadores a nível de circuitos, pulsos e algoritmos, garante ferramentas de manipulação de programas quânticos que rodam em protótipos como os dispositivos usados na IBM Experience.
Fizemos um fork do projeto de Hello World e o outro de calculadora, e reproduzimos os outputs corretos com sucesso. Essa experiência agregou uma enorme base de conhecimento sobre a parte de software que envolve a tecnologia, quebrando uma grande barreira de entrada para todos da equipe que não compreendiam o funcionamento.
Seguimos procurando compreender a biblioteca Qiskit e como poderíamos manipular sua sintaxe ao ponto de executar os circuitos quânticos e retornar um bit verdadeiramente randômico no console log.
Como todo processo de pesquisa metodológica prática e instantânea, folheamos as páginas de busca na web2 e encontramos vários assuntos relacionados e propostas de mecanismos para executar tal atividade. Aviso logo de cara que não é algo tão simples como math.random(). Aparentemente gerar um número randômico requer múltiplas camadas de algoritmos que quando compostos garantem complexos níveis de aleatoriedade. Um verdadeiro número randômico deve ser mensurado através de eventos físicos não determinísticos e fornecido como input para um algoritmo que une sua sequência de bits junto a uma sequência uniformemente aleatória.
Foi se aprofundando mais quanto a importância do hardware que deparamos com a implementação da biblioteca Qiskit que retorna no console um bloco de bits aleatórios. A biblioteca é chamada de qiskit_rng, e demonstra o exercício de gerar números pseudo randômicos usando os circuitos e simuladores disponibilizados pela IBM. Inclusive, por um momento acreditamos que o número gerado pelo qiskit_rng seria verdadeiramente randômico. Na verdade, o método proposto gera números pseudo randômicos.
Observamos em uma documentação da Qiskit, a existência da imbq_random, uma implementação em modo Beta, que aponta o uso da qiskit_rng para gerar aleatoriedade, mas que esse resultado não é forte e precisa ser extraído uma maior complexidade com ajuda da Cambridge Quantum Computing (CQC). Uma nota definindo o uso do extrator CQC, informa que nem todas as contas terão esse serviço disponível. Ao pesquisarmos sobre a empresa, descobrimos um consolidado hub de serviços quânticos de grande porte para diversas áreas de aplicações como, segurança, machine learning, química quântica etc. O seu serviço que mais chamou a atenção foi o TKET.
TKET é a líder em kit de desenvolvimento open-source que permite otimizações milimétricas e manipulação de circuitos quânticos para dispositivos NISQ, que são quantum processadores de última geração. TKET é integrado com a maioria das plataformas de hardwares como, Google, Honeywell, IonQ e até mesmo a IBM. Conforme fomos investigando e lendo a respeito, percebemos o quão grande esse hub se tornou. Conseguimos achar o setor quântico a nível de fornecedor.
Não levou muito tempo para descobrir a estrutura da árvore das relações de prestação de serviços quânticos, pois ainda são bem limitados. Então enviamos um email perguntando como funciona esse serviço e se, caso ele possa ser providenciado a pequenos laboratórios como nós, como é a precificação do uso (já estou a um bom tempo sem resposta). Na tentativa de nos inteirarmos mais sobre o assunto e quem sabe até ter uma conversa direta com algum representante.
Percebemos uma relação entre oferta e demanda, e identificamos quem possui a oferta, em seguida foi apenas questão de tempo para acharmos outras instituições que já tem acesso a estes hardwares, ou melhor ainda, que possuem seu próprio hardware quântico em laboratório, e podem providenciar o serviço de API para terceiros. Oba! É o nosso caso! Enquanto aguardamos a resposta da CQC, iremos à implementação de soluções menos burocráticas e consumidoras de tempo.
Australian National University
Acredite ou não, existe um laboratório na Austrália que gera verdadeiros números aleatórios usando lasers e sensores de alta velocidade que continuamente mensuram as flutuações no vácuo, providenciando uma infinita fonte de verdadeira entropia. Acabei encontrando o seu serviço no marketplace da AWS após enviar aquele e-mail para a Cambridge Quantum Computing.
Seu gerador de números aleatórios utiliza as ‘flutuações no vácuo', como um dado quântico. Estas flutuações são mais uma característica do mundo quântico… – É como se, na prática…fosse ‘impossível‘ não existir algo no vácuo. Mesmo na ‘escuridão absoluta’…uma energia disponível – embora que continue a ser invisível, deixa pistas que são detectáveis. Estas pistas assumem a forma de um ‘ruído quântico‘…totalmente aleatório, que surge apenas, ao se tentar medi-lo. Para visualizar este ruído, os cientistas dividiram um “feixe de laser” em partes iguais. Um “divisor de feixe” tem 2 portas de entrada e 2 de saída. A 2ª porta de entrada foi coberta, de modo a impedir a entrada da luz. Entretanto, as flutuações do ‘vácuo quântico‘ continuaram lá, influenciando a saída dos feixes parciais. Em seguida, os 2 feixes foram dirigidos aos detetores, medindo-se a intensidade do fluxo de fótons (cada fóton produz um elétron…e a corrente resultante é registrada no detetor). Ao subtrair a medição das 2 curvas produzidas pelos 2 detectores – o resultado seria zero, se estivéssemos tratando com o mundo clássico. Porém, no mundo quântico, resta o ruído quântico.
A Universidade Nacional da Austrália (ANU), garante aos seus usuários uma experiência única ao partilhar seus ruídos quânticos através de uma API, que concede gratuitamente até 100 chamadas API por mês. Mas será que apenas 100 chamadas conseguem suprir a nossa necessidade para concluir a geração de 10.000 artes randômicas?
Sua simples, porém poderosa API nos chamou atenção logo de início. Seus três únicos parâmetros são: o tipo do dado, tamanho da array e tamanho do bloco. Sendo o tamanho da array limitada até um máximo de 1024, enquanto o tamanho do bloco pode ser entre 1 e 10 somente caso o usuário opte pelos tipos ‘hex8’ ou ‘hex16’.
De acordo com a API, é possível em uma única chamada retornar um bloco contendo diversos números gerados aleatoriamente, no entanto, eles recomendam o uso de alguma técnica de extração, para criar uma sequência uniformemente randômica de maior qualidade.
Problemática
A maioria dos geradores de números físicos regulares incluem uma ou outra forma de extração de aleatoriedade para corrigir vieses e correlações que aparecem devido a imperfeições nos dispositivos de medição e geração, mesmo para boas fontes de aleatoriedade com alta entropia.
Outra camada de processo é necessária para converter a fraca fonte de entropia em um gerador de bits uniforme. Aqueles chamados extratores de aleatoriedade têm múltiplas aplicações em geradores de números pseudo random e têm aparência muito comum no assunto. Extratores determinísticos podem ser programados para produzir melhores resultados uniformes caso a sequência de entrada já tenha entropia intrínseca suficiente - como é o caso da geração quântica. O apelo é grande porque requer baixo poder de computação e hardware simples. Para ter um método eficiente e preservar o máximo de bits necessários, precisamos ter uma boa estimativa da nossa entropia disponível e, em seguida, escolher um extrator de aleatoriedade adequado (Ma et al., 2013b).
Para o nosso projeto, foram usados mais de 200 atributos, mas o total de vezes em que se faz necessário o uso de números randômicos entre 1 e 100 é de 33 vezes. Ou seja, para cada NFT gerado, precisamos de 33 números entre 1 e 100. Então precisamos de pelo menos 33.000 usos de randInt(1,100) para todos os 10.000 NFTs. Com 1024 resultados por chamada API, poderíamos terminar com apenas 33 chamadas. Mas devido ao aprendizado sobre extração para melhor qualidade randômica, elaboramos um algoritmo que contempla este requisito.
Implementando API
Encontramos no github um exemplo de implementação em python para receber uma resposta contendo as informações da API pública dos laboratórios da ANU. Após se cadastrar no seu website, adquirimos uma API Key. Inserindo os parâmetros tipo de dados e tamanho de lista, recebemos um modelo de dados no formato JSON que se parece com: “[49799, 37990, 57774, 52547, 20540, 13370…]”. Infelizmente não podemos requisitar intervalos explícitos de números aleatórios (1-100 ou 1-8). E também não seria a melhor aproximação, pois precisamos de muitos intervalos aleatórios, O tipo de chamada limita inteiros aleatórios entre 1 e 65536, usando uint16.
Caso fosse convertido cada um dos 1024 números, por chamada API, em inteiros aleatórios, seriam necessárias cerca de 40 chamadas APIs para suprir a criação de 10.000 unidades. No entanto, embora a fonte desses números sejam verdadeiramente randômicas, é necessário um tratamento dessa extração antes de seu uso para se obter aleatoriedade de maior qualidade. Começamos a criação do nosso extrator de aleatoriedade.
Conversão: uint16 => uint
Mas como vamos converter estes números aleatórios fornecidos pela ANU, em números inteiros entre 1 e 100? A equipe disputou pela melhor ideia e projetos em paralelo foram desenvolvidos e apenas o mais eficiente seria utilizado. A problemática era extrair de uma lista com 1024 inteiros entre 1 e 65536, novos inteiros randômicos entre 1 e 100. Após misturarmos as ideias, surgiu um código em conjunto, um Megazord do qual concordamos ser o mais eficiente.
A ideia consiste em transformar todos os 1024 números das chamadas em uma sequência única binária, que seria então concatenada entre todas as chamadas API’s, se tornando uma grande cadeia de bits. O que vem após pode ser um pouco complicado e pode ficar bem técnico. Nossa solução foi criar duas variáveis, uma inicial contendo a probabilidade mínima e uma contendo o tamanho da probabilidade máxima, esta será nosso bloco máximo de probabilidades e será cortado pela metade a cada iteração. Um número binário será escolhido de forma pseudo-randômica dentro da array dos números quânticos, este binário será 0 ou 1 e ele vai dizer qual direção que vamos prosseguir. Se inicialmente o 0 for escolhido, vamos ficar entre 0 e 50, se o número 1 for escolhido, será representada a escolha entre 51 e 100.
Se você pegou a ideia, já percebeu que o próximo número deve ser entre 0 e 24 ou 25 e 50 caso o primeiro binário tenha sido 0. Se por exemplo recebemos a sequência “111”, significa que após “11” teremos um bloco entre 75 e 100, mas que se tentarmos dividir o bloco por dois novamente, teremos um impasse pois 25 / 2 = 12,5. Nesse caso vamos usar o próximo número binário como critério de desempate. Ele vai decidir se o número quântico dessa seleção tende a subir ou a descer. Vamos continuar esse processo de escolha binária até que nosso bloco seja inferior a 1 e possamos então retornar o inteiro escolhido.
Esse processo permite filtrar de forma pseudo-randômicas, números quânticos, que serão usados para decidir etapas na montagem de um número inteiro. Bem maluco né? Aqui está um print do console ao buscar números aleatórios entre 1 e 100: True random number generation: 9 True random number generation: 51 True random number generation: 30 True random number generation: 20 True random number generation: 82 True random number generation: 40 True random number generation: 26 True random number generation: 8 True random number generation: 81 True random number generation: 49
O código pode ser encontrado neste link.
Extrator: Melhorando a qualidade
Após a conversão de todos os inteiros em binários e finalizada a fórmula randint, fizemos uma contagem e percebemos que nosso bloco de números aleatórios enviado pela ANU continha 53% de 1s 47% de 0s. Não satisfeitos com essa distribuição, e procurando se assimilar com a maneira como o randint convencional distribui de forma uniforme sua aleatoriedade, seriam necessárias camadas de tratamento para aperfeiçoar o processo.
Neste artigo na RPubs, é simulada a probabilidade de ocorrências de uma moeda cair cara ou coroa, e com 200 tentativas, este gráfico foi gerado:
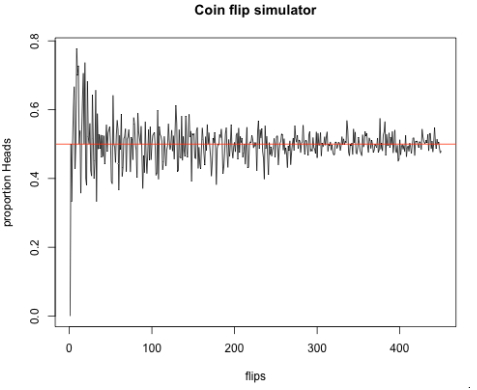
É perceptível que conforme lançamos mais moedas, a probabilidade de ser cara ou coroa se aproxima de uma proporção 50/50. Este teste é executado utilizando números pseudo randômicos e trouxemos como exemplo para mostrar que a tendência de números randômicos, que com muitas tentativas, deve se aproximar desta proporção.
Esperamos um equilíbrio próximo de 50% para ambos os valores binários. Mas não podemos ficar abusando das chamadas API para constituir um bloco maior capaz de atingir naturalmente algo em torno de tal proporção. Pois cada uma das requisições API custam U$0,005. A solução mais plausível seria a injeção de binários até que se atinja a proporção 1:1. Somos bem teimosos e criteriosos, então gostaríamos de garantir uma aleatoriedade de qualidade.
Executando o arquivo randsome_count.py, em um dos JSON retornados pela ANU, já convertidos em binários, temos: Total de 0s: 6910 Total de 1s: 7971 0s %: 46.44 1s %: 53.56
Aumentamos as chamadas para um total de 150 e o resultado não nos deixou muito contentes: Total de 0s: 1023398 Total de 1s: 1172550 0s %: 46.60 1s %: 53.39
Achamos um código em python no GitHub que contemplou nossas necessidades. Dado uma string de números binários, os faltantes da proporção deveriam ser inseridos de maneira randômica em pontos aleatórios do index. Implementamos o mesmo código, porém trocamos a função de aleatoriedade regular e usamos nosso bloco de números quânticos para decidir em qual ponto do index seriam inseridos os novos números faltantes. Então pode-se dizer, que usamos dos próprios números quânticos junto aos pseudo randômicos para expandir nosso bloco de números verdadeiramente aleatórios.
Após implementar o método de inserção, obtivemos este resultado: Total de 0s: 1172550 Total de 1s: 1172550 0s %: 50.0 1s %: 50.0
Conclusão
Obtemos um bloco com cerca de 2.3 milhões de verdadeiros números randômicos. No início dessa pesquisa, a noção sobre o nascimento de números randômicos fez-se difícil de entender, nosso conhecimento de quântica era limitado e alguns conceitos não eram nada do que pensávamos. Acontece que para gerar muitos números randômicos, é comum se usar uma frase semente para iniciar uma lógica determinística ou probabilística. Quando usamos inputs aleatórios como por exemplo, movimento de mouse ou o intervalo de tempo de acesso ao hd, e usamos esses dados como sementes dinâmicas, o extrator retorna resultados de maior qualidade, aumentando o nível de aleatoriedade do nosso bloco.
No entanto, usando o método probabilístico (Alonand Spencer, 2016), (Radhakrishnan e Ta-Shma, 2000) mostrou que sempre existem extratores com uma saída que contém quase toda a entropia oculta disponível em uma sequência de entrada vinda de qualquer fonte k. Isso permitiria uma enumeração exaustiva e possível previsibilidade da sequência, sendo claramente não válida para criptografia. Embora a aleatoriedade fraca possa ser usada com segurança com esquemas de assinatura, criptografia e outros protocolos relacionados precisam de uma chave de alta qualidade ou se tornam vulneráveis (Austrin et al., 2014; Dodis et al., 2004; Dodis e Spencer, 2002; McInnes e Pinkas, 1991).
Foram estes apelos que tornaram a utilizar os resultados do hardware quântico da ANU como frase semente para a criação de um bloco de números verdadeiramente randômicos. O bloco é então consumido toda vez que há uma requisição para gerar um número inteiro aleatório. Removendo os binários utilizados, estaremos evitando uso duplicado dos números randômicos. Sendo necessária a reposição e construção de novos blocos randômicos caso todos sejam consumidos.
A pergunta final que ainda estamos aguardando resposta da ANU é um tanto quanto filosófica. A maneira como ANU consegue seus outputs quânticos é medindo flutuações no vácuo. Sabemos que esta técnica pode retornar números verdadeiramente randômicos muito rápido. No entanto, será que estas chamadas APIs são partilhadas entre clientes? Será que os outputs são constantemente processados e enviados como respostas para diferentes usuários dando fetch. Nesse caso, haveria a possibilidade de nossos números verdadeiramente randômicos estarem sendo usados para outros propósitos desconhecidos, e vinculados ou não, concordamos que há uma certa perda de unicidade.
O experimento foi um sucesso, o gerador quântico consegue realizar cerca de 50.000 números aleatórios entre 1 e 100 com 150 chamadas API em um valor agregado de U$0,75. Vamos investigar mais a origem desses números randômicos para ter certeza de que a nossa fonte é verdadeiramente única e aleatória. Nosso repositório pode ser acessado aqui.
Se você tem alguma dúvida por onde começar, encontre a gente em nossas comunidades ou envie um email, para [email protected].
Ficaremos felizes em trabalhar com você!

