Algumas maneiras de usar ZK-SNARKs para privacidade

Artigo traduzido do original Some ways to use ZK-SNARKs for privacy https://vitalik.ca/general/2022/06/15/using_snarks.html

---

Agradecimentos especiais a Barry Whitehat e Gubsheep pelo feedback e revisão.

ZK-SNARKs são ferramentas criptográficas poderosas e uma parte cada vez mais importante dos aplicativos que as pessoas estão construindo no espaço de blockchain e além. Mas eles são complicados, tanto em termos de como funcionam, quanto em termos de como você pode usá-los.

Meu post anterior explicando ZK-SNARKs se concentrou na primeira pergunta, tentando explicar a matemática por trás dos ZK-SNARKs de uma maneira razoavelmente compreensível, mas ainda teoricamente completa. Este post se concentrará na segunda pergunta: como os ZK-SNARKs se encaixam nos aplicativos existentes, quais são alguns exemplos do que eles podem fazer, o que não podem fazer e quais são algumas diretrizes gerais para descobrir se é possível usar ZK- SNARKs em alguma aplicação em particular?

Em particular, este post se concentra na aplicação de ZK-SNARKs para preservar a privacidade.

O que um ZK-SNARK faz?

Suponha que você tenha uma input público x, uma input privado w e uma função (pública)

f(x,w)→{True,False} que realiza algum tipo de verificação nas entradas. Com um ZK-SNARK, você pode provar que conhece um w tal que f(x,w)=True para alguns dados f e x, sem revelar o valor de w. Além disso, o verificador pode verificar a prova muito mais rápido do que levaria para eles próprios calcularem f(x,w), mesmo que saibam w.

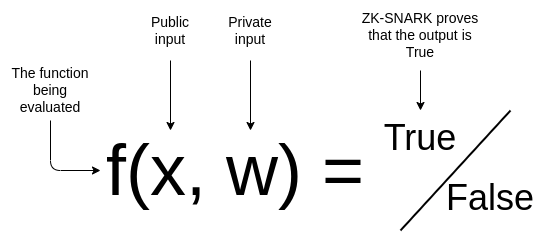
Isso dá ao ZK-SNARK suas duas propriedades: privacidade e escalabilidade. Como mencionado acima, neste post, nossos exemplos se concentrarão na privacidade.

Prova de filiação (membership)

Suponha que você tenha uma carteira Ethereum e queira provar que essa carteira possui um registro de prova de humanidade (proof-of-humanity), sem revelar qual é o seu registro humano. Podemos descrever matematicamente a função da seguinte forma:

• A input privado (w): seu endereço A, e a chave privada k para seu endereço
• A input público (x): o conjunto de todos os endereços com perfis verificados de prova de humanidade {H1 ...Hn}
• A função de verificação f(x,w):
  • Considere w como o par (A,k) e x como a lista de perfis válidos {H1...Hn}
  • Verifique se A é um dos endereços em {H1...Hn}
  • Verifique que privtoaddr(k)=A
  • Retorne True se ambas as verificações forem aprovadas, False se qualquer uma das verificações falhar

O usuário que se submete à prova (P) gera o endereço A e a chave associada k, e fornece w=(A,k) como a input privado para f. Da blockchain, eles pegam a input público, o conjunto atual de perfis com prova de humanidade verificados {H1...Hn}. Eles executam o algoritmo de prova ZK-SNARK, que gera a prova (assumindo que as entradas estão corretas). O usuário P envia a prova ao verificador e fornece a altura do bloco em que obteve a lista de perfis verificados.

O verificador também lê a blockchain, obtém a lista {H1...Hn} na altura que o usuário P especificou e verifica a prova. Se a verificação for aprovada, o verificador está convencido de que o usuário P possui algum perfil de prova de humanidade verificado.

Antes de passarmos para exemplos mais complicados, recomendo que você reveja o exemplo acima até entender cada pedacinho do que está acontecendo.

Tornando a prova de associação mais eficiente

Uma fraqueza no sistema de prova acima é que o verificador precisa conhecer todo o conjunto de perfis {H1...Hn}, e eles precisam gastar tempo O(n) "introduzindo" este conjunto no mecanismo ZK-SNARK.

Podemos resolver isso passando como input público uma raiz Merkle on-chain contendo todos os perfis (poderia ser apenas a raiz do estado). Adicionamos uma nova input privado, uma prova de Merkle M que prova que a conta do usuário que se submeteu à prova A está na parte relevante da árvore.

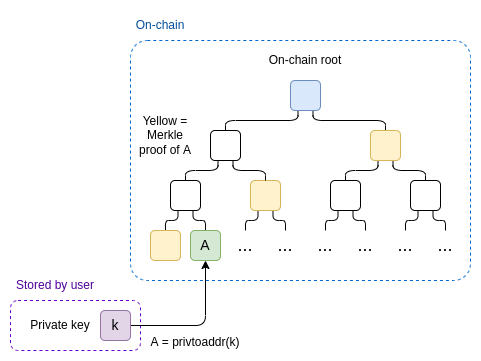
Aos leitores avançados: Uma alternativa muito nova e mais eficiente às provas de Merkle para provar a afiliação (membership) via ZK é o Caulk. No futuro, alguns desses casos de uso devem migrar para esquemas do tipo Caulk.

ZK-SNARKs para moedas

Projetos como Zcash e Tornado.cash permitem que você tenha moedas que preservam a privacidade. Agora, você poderia pensar que pode usar a "prova de humanidade ZK" acima, mas ao invés de provar o acesso a um perfil de prova de humanidade, usá-la para provar o acesso a uma moeda. Mas temos um problema: temos que resolver simultaneamente a privacidade e o problema do gasto duplo. Ou seja, não deve ser possível gastar a moeda duas vezes.

Veja como resolvemos isso. Qualquer um que tenha uma moeda tem um segredo privado s. Eles calculam localmente a "folha" (leaf) L=hash(s,1), que é publicada on-chain e se torna parte do estado, e N=hash(s,2), que chamamos de nullifier. O estado é armazenado em uma árvore Merkle.

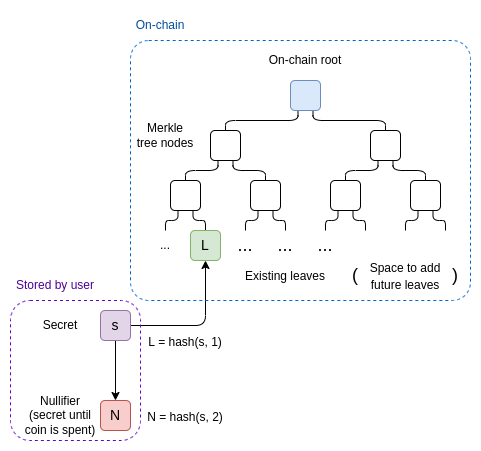
Para gastar uma moeda, o remetente deve fazer um ZK-SNARK em que:

• A input público contém um nullifier N, a raiz Merkle atual ou recente R e uma nova folha L′ (a intenção é que o destinatário tenha um segredo s′ e passe para o remetente L′=hash(s′,1))
• A input privado contém um segredo s, uma folha L e um ramo Merkle M
• A função de verificação verifica se:
  • M é um ramo Merkle válido provando que L é uma folha em uma árvore com raiz R, onde R é a raiz Merkle atual do estado
  • hash(s,1)=L
  • hash(s,2)=N

A transação contém o nullifier N e a nova folha L′. Na verdade, não provamos nada sobre L′, mas "misturamos" à prova para evitar que L′ seja modificado por terceiros quando a transação estiver em andamento.

Para verificar a transação, a blockchain verifica o ZK-SNARK e, adicionalmente, verifica se N não foi usado em uma transação de gasto anterior. Se a transação for bem-sucedida, N é adicionado ao conjunto de nullifiers gastos, para que não possa ser gasto novamente. L' é adicionado à árvore de Merkle.

O que está acontecendo aqui? Estamos usando um zk-SNARK para relacionar dois valores, L (que registra on-chain quando uma moeda é criada) e N (que registra on-chain quando uma moeda é gasta), sem revelar qual L está ligado a qual N. A conexão entre L e N só pode ser descoberta se você conhecer o segredo s que gerou ambos. Cada moeda que é criada só pode ser gasta uma vez (porque para cada L há apenas um N válido), mas a moeda que está sendo gasta em um determinado momento é mantida oculta.

Esta também é uma primitiva importante para entender. Muitos dos mecanismos que descrevemos abaixo serão baseados em um mecanismo muito semelhante de "gasto privado de uso único", embora para propósitos diferentes.

Moedas com saldos arbitrários

O texto descrito acima pode ser facilmente estendido para moedas com saldos arbitrários. Mantemos o conceito de "moedas", exceto que cada moeda tem um saldo anexo (privado). Uma maneira simples de fazer isso é garantir que a blockchain armazene para cada moeda, não apenas a folha L mas também um saldo criptografado.

Cada transação consumiria duas moedas e criaria duas novas moedas, e adicionaria dois pares ao estado (folha, saldo criptografado). O ZK-SNARK também verificaria se a soma dos saldos de entrada é igual à soma dos saldos de saída e se os dois saldos de saída são não negativos.

ZK anti-negação de serviço

Um interessante gadget anti-negação de serviço. Suponha que você tenha alguma identidade on-chain que não seja trivial de criar: pode ser um perfil de prova de humanidade, pode ser um validador com 32 ETH ou pode ser apenas uma conta com saldo de ETH diferente de zero. Poderíamos criar uma rede peer-to-peer mais resistente a DoS aceitando apenas uma mensagem se ela vier com uma prova de que o remetente da mensagem tem esse perfil. Cada perfil teria permissão para enviar até 1.000 mensagens por hora, e o perfil de um remetente seria removido da lista se o remetente trapaceasse. Mas como fazemos isso preservando a privacidade?

Primeiro, a configuração. Seja k a chave privada de um usuário; A=privtoaddr(k) é o endereço correspondente. A lista de endereços válidos é pública (por exemplo, é um registro on-chain). Até agora, isso é semelhante ao exemplo da prova de humanidade: você precisa provar que tem a chave privada para um endereço sem revelar qual. Mas aqui, não queremos apenas uma prova de que você está na lista. Queremos um protocolo que lhe permita provar que está na lista, mas que o impeça de fazer muitas provas. E por isso precisamos fazer mais algum trabalho.

Vamos dividir o tempo em epochs; cada epoch dura 3,6 segundos (portanto, 1.000 epochs por hora). Nosso objetivo será permitir que cada usuário envie apenas uma mensagem por epoch; se o usuário enviar duas mensagens na mesma epoch, ele será pego. Para permitir que os usuários enviem rajadas ocasionais de mensagens, eles podem usar epochs no passado recente, portanto, se algum usuário tiver 500 epochs não utilizadas, ele poderá usar essas epochs para enviar 500 mensagens de uma só vez.

O protocolo

Começaremos com uma versão simples: usamos nullifiers. Um usuário gera um nullifier com N=hash(k,e), onde k é sua chave e e é o número da epoch, e o publica junto com a mensagem m. O ZK-SNARK mais uma vez se mistura usando hash(m) sem verificar nada sobre m, de modo que a prova é vinculada a uma única mensagem. Se um usuário fizer duas provas vinculadas a duas mensagens diferentes com o mesmo nullifier, ele poderá ser pego.

Agora, vamos passar para a versão mais complexa. Em vez de apenas tornar mais fácil provar se alguém usou a mesma epoch duas vezes, esse próximo protocolo revelará sua chave privada nesse caso. Nossa técnica principal se baseará no truque "dois pontos formam uma reta": se você revelar um ponto em uma reta, revelou pouco, mas se revelar dois pontos em uma reta, revelou a reta inteira.

Para cada epoch e, tomamos a reta Le(x) = hash(k,e) ∗ x + k. A inclinação da reta é hash(k,e) e a interseção com y é k; nenhum deles é conhecido do público. Para fazer um certificado para uma mensagem m, o remetente fornece y = Le(hash(m)) = hash(k,e) ∗ hash(m) + k, juntamente com um ZK-SNARK provando que y foi calculado corretamente.

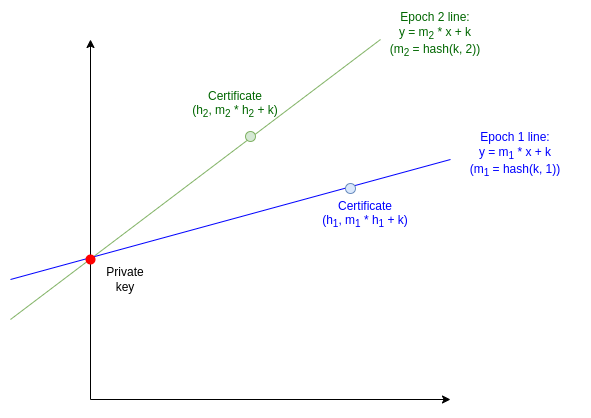
Para recapitular, o ZK-SNARK aqui é como abaixo:

• Input público:
  • {A1...An}, a lista de contas válidas
  • m, a mensagem que o certificado está verificando
  • e, o número de epochs usado para o certificado
  • y, a avaliação da função de reta
• Input privado:
  • k, sua chave privada
• Função de verificação:
  • Verifica se privtoaddr(k) está em {A1...An}
  • Verifica se y = hash(k,e) ∗ hash(m) + k

Mas e se alguém usar uma única epoch duas vezes? Isso significa que eles publicaram dois valores m1 e m2 e os valores de certificado correspondentes y1 = hash(k,e) ∗ hash(m1) + k, e y2 = hash(k,e) ∗ hash(m2) + k. Podemos usar os dois pontos para recuperar a reta e, portanto, a interseção em y (que é a chave privada):

k = y1 − hash(m1) ∗ (y2 − y1)/(hash(m2) − hash(m1))

Então, se alguém reutiliza uma epoch, eles vazam sua chave privada para todos verem. Dependendo da circunstância, isso pode implicar em fundos roubados, um validador sofrendo slashing ou simplesmente a chave privada sendo transmitida e incluída em um smart contract, ponto em que o endereço correspondente seria removido do conjunto.

O que realizamos aqui? Um sistema viável anti-negação de serviço anônimo e off-chain, útil para sistemas como redes de blockchain peer-to-peer, aplicativos de bate-papo, etc., sem exigir qualquer prova de trabalho. O projeto RLN (rate limit nullifier) ​​está construindo essa ideia atualmente, embora com pequenas modificações (ou seja, eles fazem tanto o nullifier quanto a técnica de dois pontos em uma reta, usando o nullifier para facilitar a captura de duplo-uso de uma epoch).

Reputação negativa de ZK

Suponha que queremos construir o 0chan, um fórum na internet que fornece anonimato total como o 4chan (para que você nem tenha nomes persistentes), mas que tenha um sistema de reputação para incentivar conteúdos de qualidade melhor. Este pode ser um sistema em que alguma DAO de moderação possa sinalizar postagens com violação de regras do sistema e instituir um mecanismo de três-strikes-e-você-está-fora; há muitas configurações.

O sistema de reputação pode apoiar a reputação positiva ou negativa; no entanto, o suporte à reputação negativa requer infraestrutura adicional para exigir que o usuário leve em consideração todas as mensagens de reputação em sua prova, mesmo as negativas. É neste caso de uso mais difícil, semelhante ao que está sendo implementado com o Unirep Social, que nos concentraremos.

Encadeamento de posts: o básico

Qualquer um pode fazer um post publicando uma mensagem on-chain que contém o post, e um ZK-SNARK provando que (i) você possui alguma identidade externa escassa, por exemplo, prova de humanidade, que lhe dá direito a criar uma conta, ou (ii) que você fez anteriormente algum post específico. Especificamente, o ZK-SNARK é o seguinte:

• Inputs públicas:
  • O nullifier N
  • Uma raiz de estado da blockchain recente R
  • O conteúdo do post ("misturado" à prova para vinculá-lo ao post, mas não fazemos nenhum cálculo nele)
• Inputs privadas:
  • Sua chave privada k
  • Uma identidade externa (com endereço A), ou o nullifier Nprev usado no post anterior
  • A Prova de Merkle M provando a inclusão de A ou Nprev na blockchain
  • O número i de postagens que você fez anteriormente com esta conta
• Função de verificação:
  • Verifique se M é um ramo Merkle válido provando que (ou A ou Nprev, o que for fornecido) é uma folha em uma árvore com raiz R
  • Verifique se N = enc(i,k), onde enc é um função de criptografia (ex. AES)
  • Se i = 0, verifique se A = privtoaddr(k), caso contrário verifique se Nprev = enc(i−1,k)

Além de verificar a prova, a blockchain também verifica se (i) R na verdade é uma raiz de estado recente e (ii) o nullifier N ainda não foi usado. Até agora, isso é como a moeda de preservação de privacidade apresentada anteriormente, mas adicionamos um procedimento para "cunhar" (minting) uma nova conta e removemos a capacidade de "enviar" sua conta para uma chave diferente - em vez disso, todos os nullifiers são gerados usando sua chave original.

Usamos enc em vez de hash aqui para tornar os nullifiers reversíveis: se você tiver k, você pode descriptografar qualquer nullifier específico que você vê on-chain e se o resultado for um índice válido e não um lixo aleatório (por exemplo, poderíamos apenas verificar dec(N)<2^64), então você sabe que o nullifier foi gerado usando k.

Adicionando reputação

A reputação neste esquema é on-chain e clara: alguns smart contracts têm um método addReputation, que recebe como entrada (i) o nullifier publicado junto com o post e (ii) o número de unidades de reputação a serem adicionadas e subtraídas.

Ampliamos os dados on-chain armazenados por post: em vez de apenas armazenar o nullifier N, armazenamos {N,h¯,u¯}, onde:

• h¯ = hash(h,r) onde h é a altura do bloco do raiz do estado que foi referenciada na prova
• u¯ = hash(u,r) onde u é a pontuação de reputação da conta (0 para uma conta nova)

r aqui é simplesmente um valor aleatório, adicionado para evitar que h e u sejam descobertos por uma busca brute-force (no jargão de criptografia, adicionar r torna o hash um compromisso oculto).

Suponha que um post use uma raiz R e armazene {N,h¯,u¯}. Na prova, ele está vinculado a um post anterior, com dados armazenados {Nprev,h¯prev,u¯prev}. A prova do post também é necessária para percorrer todas as entradas de reputação que foram publicadas entre hprev e h. Para cada nullifier N, a função de verificação descriptografaria N usando a chave do usuário k, e se a descriptografia gerasseum índice válido, aplicaria a atualização de reputação. Se a soma de todas as atualizações de reputação for δ, a prova finalmente verificaria u = uprev + δ.

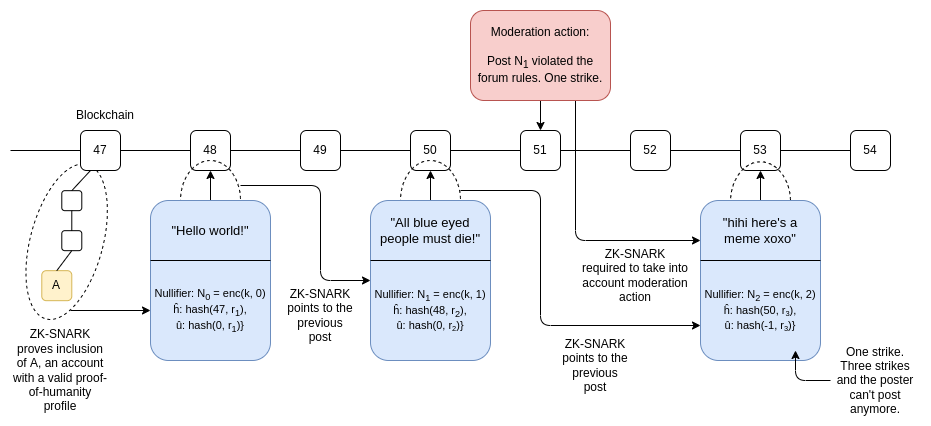
Se quisermos uma regra de "três-strikes-e-você-está-fora", o ZK-SNARK também verificaria u > −3. Se quisermos uma regra em que um post possa receber um sinalizador especial "criador de post de alta reputação" se o criador de post tiver ≥ 100 rep, podemos adaptar isso adicionando "é u ≥ 100?" como input público. Podem ser acomodados muitos tipos de regras.

Para aumentar a escalabilidade do esquema, poderíamos dividi-lo em dois tipos de mensagens: postagens e reconhecimentos de atualização de reputação (RCAs - reputation update acknowledgements). Um post seria off-chain, embora fosse necessário apontar para um RCA feito na semana passada. Os RCAs seriam on-chain e um RCA percorreria todas as atualizações de reputação desde o RCA anterior desse criador do post. Dessa forma, a carga on-chain é reduzida para uma transação por criador do post por semana mais uma transação por mensagem de reputação (um nível muito baixo se as atualizações de reputação forem raras, por exemplo, elas são usadas apenas para ações de moderação ou talvez prêmios no estilo "post do dia").

Responsabilizando as partes centralizadas

Às vezes, você precisa construir um esquema que tenha algum tipo de "operador" central. Isso pode ocorrer por vários motivos: algumas vezes é por escalabilidade, outras, por privacidade - especificamente, a privacidade dos dados mantidos pelo operador.

O MACI, por exemplo, exige que os eleitores enviem seus votos on-chain criptografados para uma chave secreta mantida por um operador central. O operador descriptografaria todos os votos on-chain, os contaria e revelaria o resultado final, juntamente com um ZK-SNARK provando que eles fizeram tudo corretamente. Essa complexidade extra é necessária para garantir uma forte propriedade de privacidade (chamada de resistência à coerção): que os usuários não possam provar aos outros como votaram, mesmo que quisessem.

Graças a blockchains e ZK-SNARKs, a quantidade de confiança no operador pode ser mantida muito baixa. Um operador malicioso ainda pode quebrar a resistência à coerção, mas como os votos são publicados na blockchain, o operador não pode trapacear censurando votos e, como o operador deve fornecer um ZK-SNARK, ele não pode trapacear calculando incorretamente o resultado.

Combinando ZK-SNARKs com MPC

Um uso mais avançado de ZK-SNARKs envolve fazer provas sobre cálculos onde as entradas são divididas entre duas ou mais partes, e não queremos que cada parte aprenda as entradas das outras partes. Você pode satisfazer o requisito de privacidade com circuitos ilegíveis (garbled circuits) no caso de 2 partes, e, no caso de N partes, com protocolos de computação de multi-partes mais complicados. Os ZK-SNARKs podem ser combinados com esses protocolos para fazer computação multipartidária verificável.

Isso pode permitir sistemas de reputação mais avançados, onde vários participantes podem realizar cálculos conjuntos sobre suas entradas privadas, pode permitir mercados de dados autenticados, mas que preservem a privacidade, e muitos outros aplicativos. Dito isso, observe que a matemática para fazer isso com eficiência ainda está relativamente em sua infância.

O que não podemos tornar privado?

ZK-SNARKs geralmente são muito eficazes para criar sistemas onde os usuários têm estado privado. Mas os ZK-SNARKs não podem manter um estado privado que ninguém conhece. Para fazer uma prova sobre uma informação, o usuário que se submete à prova precisa conhecer essa informação em texto simples (não criptografado).

Um exemplo simples do que não pode ser privado (facilmente) é a Uniswap. Na Uniswap, há uma única "coisa" com a lógica central, a conta do formador de mercado (market maker), que não pertence a ninguém, e cada negociação na Uniswap está sendo negociada contra a conta do criador de mercado. Você não pode esconder o estado da conta do formador de mercado, porque então alguém teria que manter o estado em texto claro para fazer provas, e seu envolvimento ativo seria necessário em cada transação.

Você poderia fazer uma Uniswap operada centralmente, segura e privada, com circuitos ilegíveis ZK-SNARK, mas não está claro se os benefícios de fazer isso valeriam os custos. Pode até não haver nenhum benefício real: o contrato precisaria ser capaz de informar aos usuários quais são os preços dos ativos, e as mudanças bloco a bloco nos preços dizem muito sobre qual é a atividade de negociação.

Blockchains podem tornar as informações de estado globais, ZK-SNARKs podem tornar as informações de estado privadas, mas realmente não temos nenhuma boa maneira de tornar as informações de estado globais e privadas ao mesmo tempo.

Ajuste: você pode usar computação multipartidária para implementar o estado privado compartilhado. Mas isso requer uma suposição de limite de maioria honesta, o que é provavelmente instável na prática porque (ao contrário, por exemplo, de ataques de 51%) uma maioria mal-intencionada pode conspirar para quebrar a privacidade sem nunca ser detectada.

Juntando as primitivas

Nas seções acima, vimos alguns exemplos que são ferramentas poderosas e úteis por si só, mas também servem como blocos de construção em outros aplicativos. Nullifiers, por exemplo, são importantes para moeda, mas acontece que eles aparecem de novo e de novo em todos os tipos de casos de uso.

A técnica de "encadeamento forçado" usada na seção de reputação negativa é amplamente aplicável. É eficaz para muitos aplicativos em que os usuários possuem "perfis" complexos que mudam de maneira complexa ao longo do tempo e você deseja forçar os usuários a seguir as regras do sistema, preservando a privacidade para que ninguém veja qual usuário está executando qual ação. Os usuários podem até ser obrigados a ter árvores Merkle privadas inteiras representando seu "estado" interno. O gadget "grupo de compromissos" (commitment pool) proposto neste post pode ser construído com ZK-SNARKs. E se algum aplicativo não puder ser totalmente on-chain e precisar ter um operador centralizado, as mesmas técnicas podem ser usadas para também manter o operador honesto.

ZK-SNARKs são uma ferramenta realmente poderosa para combinar os benefícios de responsabilidade e privacidade. Eles têm seus limites, embora em alguns casos o design inteligente de aplicativos possa contornar esses limites. Espero ver muitos outros aplicativos usando ZK-SNARKs e, eventualmente, aplicativos combinando ZK-SNARKs com outras formas de criptografia, a serem construídos nos próximos anos.