Vulnerabilidades de Maleabilidade de Assinatura em Contratos Inteligentes

Prefácio

Este é o terceiro de uma série de artigos sobre vulnerabilidades às quais os contratos inteligentes são suscetíveis. Você pode encontrar meus artigos neste tópico, seguindo os links.

1. Dependência de ordem de transação
2. Reentrância
3. Maleabilidade de Assinatura [Este artigo]
4. Vulnerabilidades aritméticas

Este artigo é mais longo do que o habitual porque há muitos pré-requisitos de conhecimentos necessários para entender esta vulnerabilidade específica. Fiz o melhor que pude para explicar o básico de forma concisa para manter as coisas curtas. Por favor, use este artigo como um ponto de partida para seu empreendimento de pesquisa.

Como sempre, o objetivo principal destes artigos não é ensinar os outros, mas testar a profundidade do meu próprio entendimento. Dito isto, espero que meus trabalhos tenham até mesmo um pequeno impacto positivo sobre os outros nesta jornada comigo.

Conteúdo

1. Criptografia Básica
2. Criptografia na Ethereum
3. Visão geral da maleabilidade de assinaturas
4. Risco de segurança
5. Medidas de atenuação
6. Referências

1. Criptografia Básica

A criptografia é um ramo da matemática que é amplamente utilizado em todos os aspectos da ciência da computação, incluindo a tecnologia de blockchains. Vamos estabelecer as definições de alguns conceitos importantes antes de continuarmos.

1.1 Hashing

Hashing é o processo de receber dados e produzir uma saída única (conhecida como hash ou digest). Mesmo pequenas mudanças na entrada podem alterar significativamente a saída. Esta propriedade de funções de hashing torna útil detectar adulterações nas mensagens. Também é praticamente impossível extrair a mensagem original através do hash.

1.2 Encriptação

A encriptação é a arte da escrita secreta, ou seja, a codificação de dados em uma forma ilegível, exceto para aqueles envolvidos na comunicação. Cada parte tem acesso à(s) chave(s) para conseguir isso. Podemos pensar nisso como escrever uma carta em um idioma que só o remetente e o destinatário entendem.

Quando uma única chave é utilizada tanto para fins de criptografia quanto de decriptação, é conhecida como criptografia simétrica.

 
Embora conveniente, não é recomendado do ponto de vista da segurança. A transmissão da chave através de redes públicas não é ideal, pois pode ser interceptada e pode permitir que os maus atores escutem e modifiquem nossas mensagens..

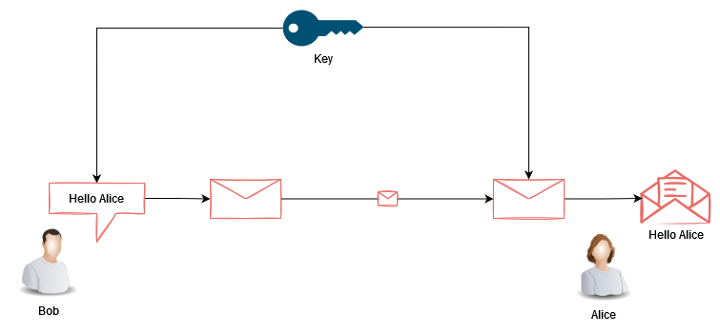
Para remediar isso, a criptografia de chave Pública foi apresentada. A criptografia de chave pública (também conhecida como criptografia assimétrica) utiliza um par de chaves para fins de criptografia e decodificação. Especificamente, a chave privada é usada para criptografar enquanto sua chave pública associada é usada para decodificar os dados criptografados pela chave privada. (Embora o inverso também seja possível).

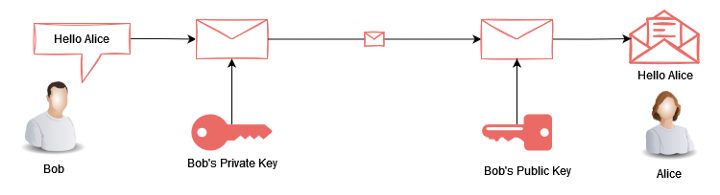
Como o nome sugere, a chave pública pode ser compartilhada livremente, sem implicações de segurança. Enquanto que, a chave privada nunca deve ser compartilhada.

1.3 Assinatura Digital

O processo de assinatura digital utiliza as técnicas discutidas acima para fornecer um método pelo qual os destinatários possam verificar a identidade do remetente. A ilustração a seguir delineia o processo de assinatura digital.

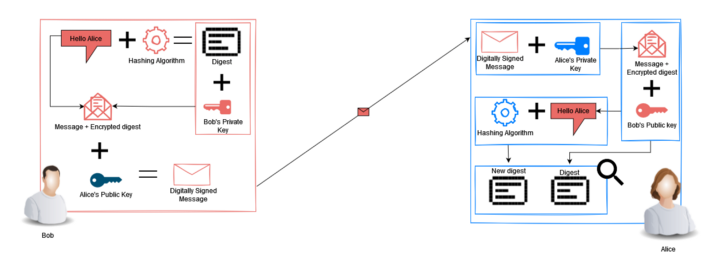
1. A Mensagem recebe um hash.
2. O código é criptografado com a chave privada do Bob.
3. O hash criptografado é então concatenado com a mensagem de texto simples original.
4. Esta nova combinação é criptografada com a chave pública da Alice.
5. Alice decodifica a mensagem com sua chave privada, e agora tem a mensagem de texto simples e o hash criptografado.
6. Alice decodifica o hash criptografado com a chave pública do Bob.
7. Alice computa o hash da mensagem de texto simples e compara o resultado.

Junto com a confidencialidade e a integridade, a não rejeição também é alcançada. Isto porque ninguém além do Bob tem acesso a sua chave privada.

2 Criptografia na Ethereum

A criptografia da Ethereum deriva fortemente da Blockchain do Bitcoin. Ambas blockchains usam criptografia de curva elíptica (ECC) e algoritmo de assinatura digital de curva elíptica (ECDSA) para geração/encriptação de chaves e assinatura digital, respectivamente. Para o hashing, a Ethereum usa KECCAK-256 enquanto o bitcoin usa SHA-256.

Vamos dar uma olhada de perto em como a ECC e o ECDSA funcionam antes de continuar. As seguintes seções possuem matemática pesada, portanto, consulte a seção de referência para mais pesquisas.

2.1 Visão Geral da Criptografia de Curva Elíptica

A Criptografia de Curva Elíptica (ECC) é um sistema de criptografia de chave pública, assim como o RSA. Entretanto, ao contrário do RSA, a ECC se enquadra na categoria de sistema criptográfico logarítmico discreto. Para o mesmo comprimento de chave, a ECC oferece maior segurança do que o RSA.

As curvas elípticas são definidas pela equação:

y² = x³+ax+b

 
No caso do Bitcoin (e da Ethereum), é utilizada a curva elíptica secp256k1, que é definida pela equação:

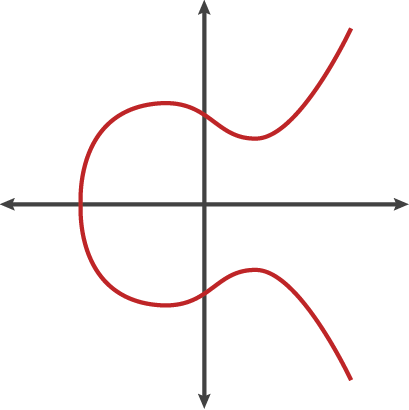
y² = x³+7

De acordo com Satoshi, não havia nenhuma razão particular para isto. (embora os céticos acreditem que é porque o secp256k1 tinha menos probabilidade de ser invadido pela NSA-Agência de Segurança Nacional).

Uma coisa a ter em mente é que as curvas elípticas são simétricas em relação ao eixo X. Outro aspecto importante das curvas elípticas que precisamos saber é que, qualquer linha reta que cruze a curva cruzará um máximo de três pontos. Isto será importante para entender as seções posteriores.

Agora que temos uma compreensão básica das curvas elípticas, vamos dar uma olhada nas operações matemáticas que podemos realizar.

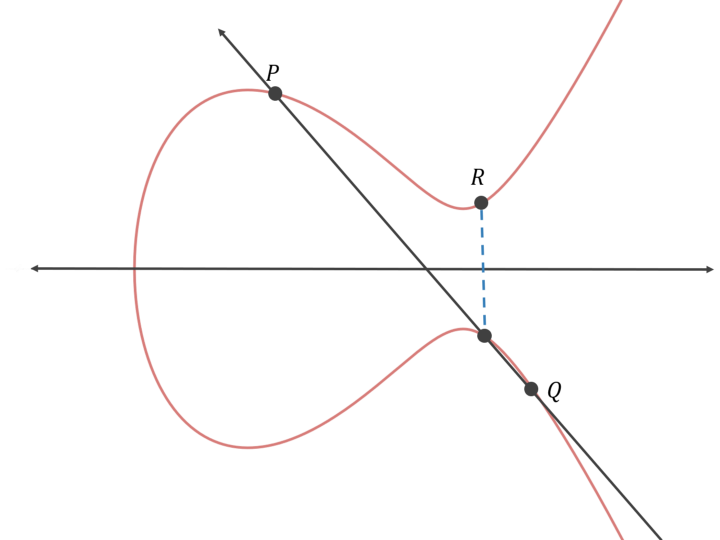
2.1.1 Adição de pontos

Suponha que tenhamos uma linha que intersecta a curva em três pontos. A soma de dois pontos de interseção no segmento de linha resultará na terceira interseção. Matematicamente;

P + Q = -R
or , P + Q + R = 0

 
Aqui, o segmento de linha intersecta a curva nos pontos P, Q e -R. O reflexo de -R (isto é, R) é igual a P + Q.
 
2.1.2 Multiplicação Escalar

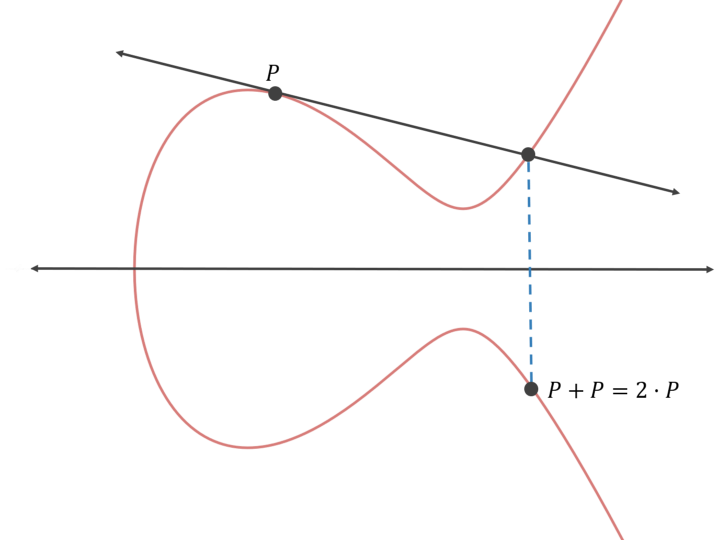
Em matemática, a multiplicação escalar refere-se à multiplicação de um vetor com um número real para obter outro vetor. No caso de curvas elípticas, podemos adicionar um ponto (P) a ele mesmo várias vezes para obter um ponto válido diferente (Q) na curva. Para isso, precisamos traçar uma tangente através do ponto. Matematicamente,

Q = P + P + .... + P
or, Q = KP

Onde, K é o número de vezes que P foi adicionado.

 
2.1.3 Geração de chave

Agora que temos um entendimento básico por trás da matemática das curvas elípticas, vamos dar uma olhada em como as chaves são geradas. O ponteiro base da curva elíptica secp256k1 tem a seguinte coordenada.

For x-coordinate: 55066263022277343669578718895168534326250603453777594175500187360389116729240
y-coordinate:32670510020758816978083085130507043184471273380659243275938904335757337482424

O ponteiro base é um escalar multiplicado com um grande valor "K" aleatório. Este valor K é nossa chave privada. O ponto resultante após a multiplicação escalar é nossa chave pública.

Depois de considerar tudo isso, uma série de perguntas. Como a ECC é adequada para criptografia?

Para responder a isto, devemos entender o conceito de funções Trapdoor. Funções Trapdoor são funções especiais que são fáceis de calcular de uma maneira, mas difíceis de calcular ao contrário, ou seja, é difícil calcular o inverso da função. Embora não impossível, os supercomputadores atuais levariam milhões de anos para computar.

No caso do RSA, é trivial encontrar o produto de dois grandes números primos, porém, é significativamente mais difícil encontrar os fatores primos de um determinado número. Esta é a função Trapdoor do RSA.

Na ECC, o produto escalar é a função Trapdoor. Dado P e K, é fácil encontrar Q. Entretanto, dado P e Q, é difícil encontrar K. Esta propriedade o torna adequado para uso em criptografia. Isto também é conhecido como o problema do logaritmo discreto.

2. Assinaturas na Ethereum

Na Ethereum, a criptografia de chave pública é utilizada para determinar a propriedade das contas (EOA). Especificamente, a chave pública fornece o controle da conta acessível ao público (o endereço) e a chave privada é usada para iniciar e assinar transações. A chave pública pode ser pensada como um número de conta bancária, enquanto a chave privada pode ser pensada como o PIN.

Por este motivo, as chaves privadas nunca são transmitidas ou armazenadas na Ethereum, ou seja, as chaves privadas nunca aparecem nas mensagens nem são armazenadas on-chain. Isto porque qualquer pessoa com uma cópia da chave privada tem o controle total da conta associada.

2.1 Visão geral da ECRECOVER

Como mencionado acima, a EVM não armazena chaves privadas on-chain, portanto não tem capacidade de assinar transações - apenas os clientes são capazes de fazer isso. Entretanto, a EVM tem a funcionalidade de verificar assinaturas. A ecrecover na Solidity é usada para isso.

A ecrecover é um contrato pré-compilado disponível para os nós. Ele é usado para executar a função de recuperação da chave pública em criptografia de curva elíptica, ou seja, recuperar uma chave pública (endereço) de uma determinada assinatura. Vamos ver o seguinte trecho de código para uma melhor compreensão.

// SPDX-License-Identifier: MIT
pragma solidity ^0.8.0;

contract recover {
  function recover(uint8 v, bytes32 r, bytes32 s, bytes32 hash) external {
    address signer = ecrecover(hash, v, r, s);
    require( signer !=address(0), "invalid ECDSA signature");
  }
}

O contrato acima é simples. Aqui, vemos que a ecrecover aceita quatro argumentos. r, s e hash são do tipo bytes32 onde, como v é um uint., ecrecover devolverá o endereço (chave pública) da conta que foi usada para assinar a transação.

4. Risco de segurança

Todas as transações precisam ser assinadas antes de serem incluídas na blockchain. Como lembramos, há quatro parâmetros necessários para a ecrecover. Um invasor pode modificar estes parâmetros (v, r e s) e ainda obter uma assinatura válida diferente, sem ter acesso à chave privada do signatário original. Isto acontece porque as curvas elípticas são simétricas, e para cada valor de v,r e s, haverá um conjunto diferente de v, r e s que têm a mesma relação.

Isto pode causar problemas se as assinaturas estiverem sendo verificadas apenas em nível contratual. Vamos dar uma olhada em um exemplo para entender melhor a vulnerabilidade.

Suponha que Alice inicia uma transação e a assina com sua chave pública. A transação é propagada por toda a rede para ser minerada e incluída no livro razão. Entre os destinatários está Bob, que é uma ameaça, e ele quer realizar um ataque de maleabilidade da transação contra Alice. Ele modificará os parâmetros v, r e s para obter uma nova assinatura válida e usar técnicas de front running (discutido aqui).

Entretanto, Bob não pode modificar os detalhes da transação tais como o montante, o destinatário ou o remetente. Nenhum dinheiro extra será deduzido da carteira da Alice e Bob também não receberá nenhum dinheiro da Alice. Isto porque tudo o que ele pode modificar é a assinatura da transação que está incluída na blockchain. Então, qual é o objetivo?

Vamos dizer que a Alice queira comprar um NFT por 1 ether. Seu aplicativo de carteira irá criar uma transação e assiná-la para ela. O aplicativo de carteira então procurará sua transação na blockchain para verificar se ela foi bem sucedida. Mas Bob mudou a assinatura da transação e esta transação modificada foi minerada em um bloco e incluída no livro razão.

Embora o pagamento tenha sido efetuado, a carteira de Alice nunca recebeu a confirmação, portanto, ela inicia a transação novamente. Este processo pode continuar até que todos os fundos se esgotem. Embora não confirmado, isto é o que se acredita ter acontecido com o Mt Gox.

5. Medida de Atenuação

A maneira mais simples e direta de evitar vulnerabilidades de maleabilidade de assinatura seria usar a biblioteca OpenZeppelin ECDS .

Muitas vezes é recomendado não reinventar a roda e reutilizar o código que foi testado meticulosamente para falhas de segurança.

6. Referências

1. https://hackernoon.com/what-is-the-math-behind-elliptic-curve-cryptography-f61b25253da3
2. https://eklitzke.org/bitcoin-transaction-malleability
3. https://journal0xrusowsky.substack.com/p/digital-signatures-ecrecover
4. https://coders-errand.com/digital-signatures/
5. https://www.youtube.com/watch?v=F3zzNa42-tQ
6. https://swcregistry.io/docs/SWC-117
7. https://github.com/ethereumbook/ethereumbook/blob/develop/04keys-addresses.asciidoc

Esse artigo foi escrito por Aayushman Thapa Magar e traduzido por Fátima Lima. Seu original pode ser lido aqui.