Esse artigo foi escrito por: Alan e traduzido por Dimitris Calixto, artigo original disponível aqui
Sumário
1 . Introdução
2 . Implementação do JavaScript
4 . Implementação do smart contract
Introdução
Merkle Trees têm sido uma faceta nos campos da criptografia e da informática mesmo antes da blockchain que hoje conhecemos e amamos existir. Hoje em dia, estamos lentamente começando a vê-las tornarem-se mais frequentemente utilizadas on-chain para fins de verificação de dados. Neste artigo, explicarei como as Merkle Trees podem ser implementadas em um contexto NFT (ERC-721) para efeitos de whitelists de tokens e como podem dar garantias de que os tokens só podem ser resgatados pelos participantes pretendidos.
Mas, o que é uma Merkle Tree!?
As Merkle Trees são uma estrutura semelhante a árvores onde cada nó da árvore é representado por um valor que é o resultado de alguma função criptográfica de hash. As funções hash são de 1 via, o que significa que é fácil produzir uma saída a partir de uma entrada, mas computacionalmente inviável para determinar uma entrada a partir de uma saída. As Merkle Trees apresentam 3 tipos de nós, sendo esses:
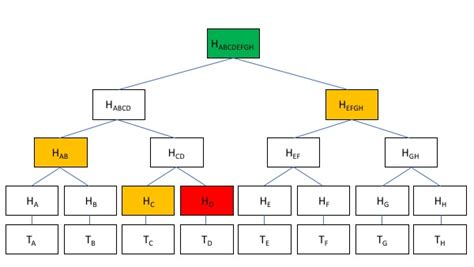
- Nós de folhas: Estes nós situam-se no fundo da árvore e o seu valor é o resultado do hash dos dados originais de acordo com uma função hash especificada. Há tantos nós de folhas numa árvore para tantos shards de dados originais que requerem hashing. Por exemplo, se 7 shards de dados necessitarem de hash, haverá 7 nós de folhas.
- Nós Parentais: Os nós pais podem sentar-se a vários níveis da árvore, dependendo do tamanho geral da árvore, mas residirão sempre acima dos nós da folha. Os nós pais só promoverão um mínimo de um nó e um máximo de dois nós. O valor de um nó pai é determinado pelo hash dos hashes concatenados de nós abaixo dele, tipicamente começando da esquerda para a direita. Uma vez que inputs diferentes produzirão sempre hashes diferentes, ignorando a colisão de hashes, é importante a ordem em que os hashes dos nós fostering são concatenados. Vale a pena mencionar que os nós pais podem fomentar outros nós pais, dependendo do tamanho da árvore.
- Nó Raiz: O nó raiz situa-se no topo da árvore e é derivado do hash dos hashes concatenados dos dois nós pais que se situam abaixo dela, novamente começando da esquerda para a direita. Existe apenas um único nó raiz em qualquer Merkle Tree e o nó raiz possui o hash raiz.
Sei que é muita informação para digerir, por isso, consulte o diagrama abaixo (Figura 1) para uma melhor visualização de como estas árvores estão estruturadas.
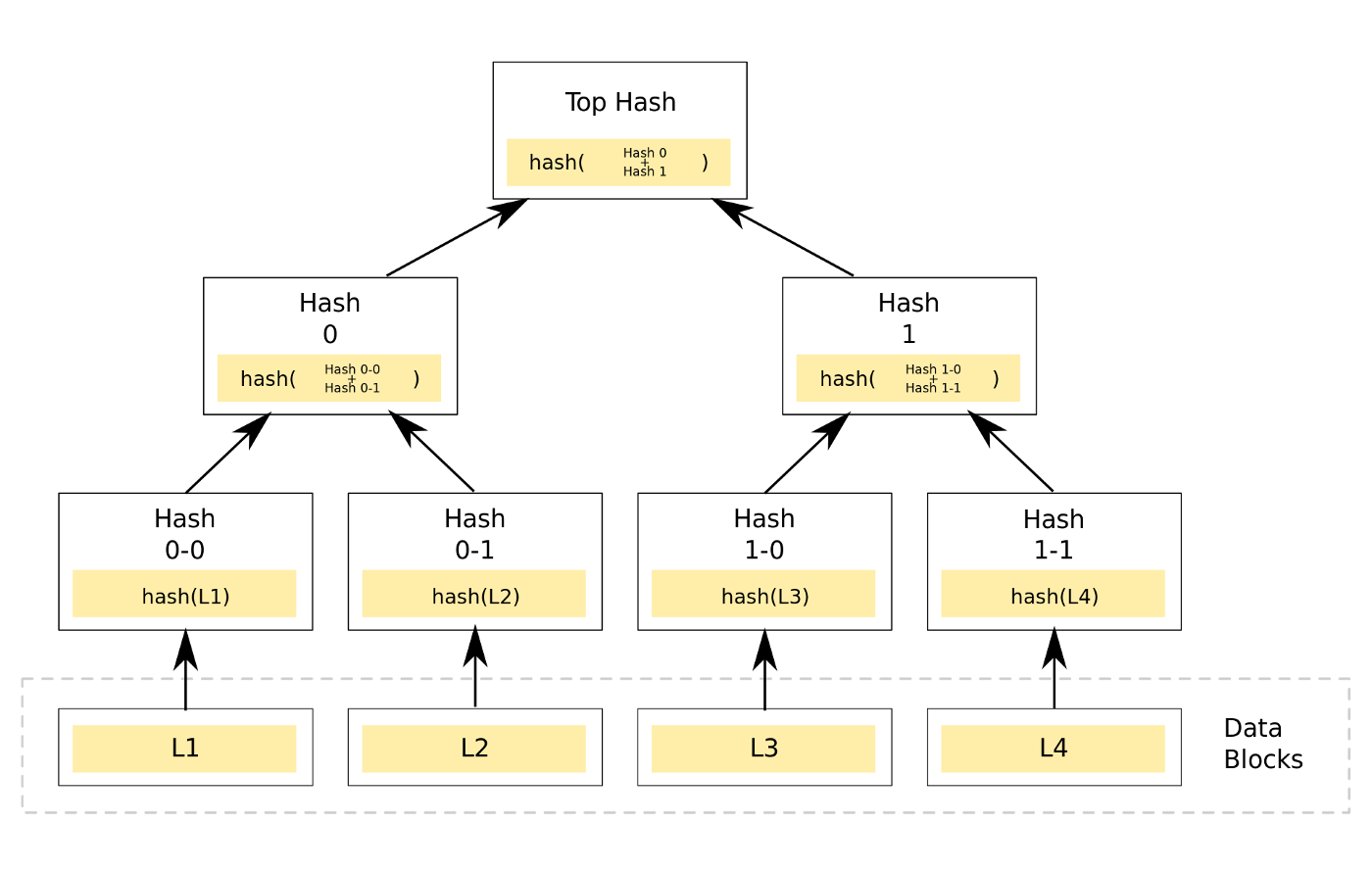Contexto
Como mencionado anteriormente, a utilização de uma Merkle Tree num contexto NFT (ERC-721) seria útil em situações em que alguma quantidade de tokens tenha sido reservada para um grupo selecionado de participantes, uma whitelist. As Merkle Trees devem ser pré-calculadas e, portanto, utilizar alguma forma de dados que seja distinta por membro. Neste contexto, digamos que um único nó de folha representa um único endereço de carteira na nossa whitelist.
Imaginemos que o seu projeto implementou uma estratégia de whitelist em que um número arbitrário de tokens foi reservado para endereços de carteira selecionados que podem ter sido escolhidos através de um concurso, sorteio, ou algum outro sistema. A estes endereços da whitelist foi concedida a possibilidade de adquirir seus tokens reservados em algum momento antes da casa da moeda pública, por uma variedade de razões. Estas podem estar relacionadas com a necessidade de evitar elevadas taxas de gas, recompensar a criatividade, participação precoce, envolvimento da comunidade, etc.
Uma vez que estes endereços são conhecidos e constantes, podemos utilizar esta informação para criar uma Merkle Tree. Para demonstrar isto, vamos utilizar as bibliotecas merkletreejs e keccak256 JavaScript. Nota: Por uma questão de simplicidade, utilizarei apenas 7 endereços de carteira para manter o tamanho da árvore conciso.
Implementação do JavaScript
A primeira coisa que queremos fazer é derivar os nossos nós de folha. Se você se lembrar, cada nó pai que se senta diretamente por cima dos nós de folha de uma árvore só irá fomentar um máximo de dois nós de folha. Se existir um número ímpar de nós-folha, um nó pai irá fomentar um único nó-folha. Cada nó de folha deve ser uma forma de dados misturados, por isso, para este exemplo, vamos usar a biblioteca keccak 256 para hash todos os endereços da nossa whitelist (Figura 2). Estamos utilizando este algoritmo de hash específico, uma vez que será utilizado mais tarde no nosso smart contract de Solidity.
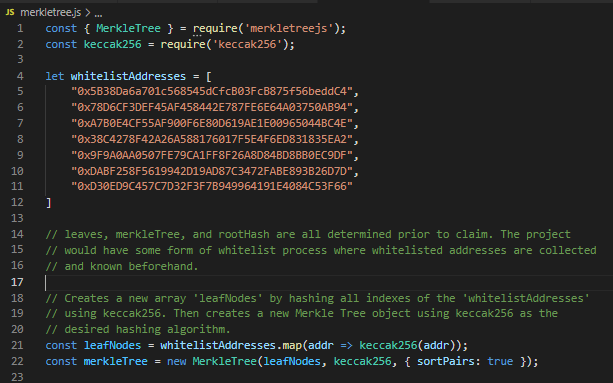
Uma vez misturados todos os endereços na nossa whitelist, obtendo assim os nossos nós de folhas, estamos agora em condições de criar o objeto Merkle Tree. Nós fazemos isso utilizando a biblioteca MerkleTreeJs e chamando a função new MerkleTree(), passando os nossos nós de folha como o primeiro argumento, o nosso algoritmo de hashing como o segundo, e a opção { sortPairs: true } como a última. O argumento final é opcional, mas encontrei grande dificuldade em tentar fazer esse exemplo funcionar sem utilizá-lo.
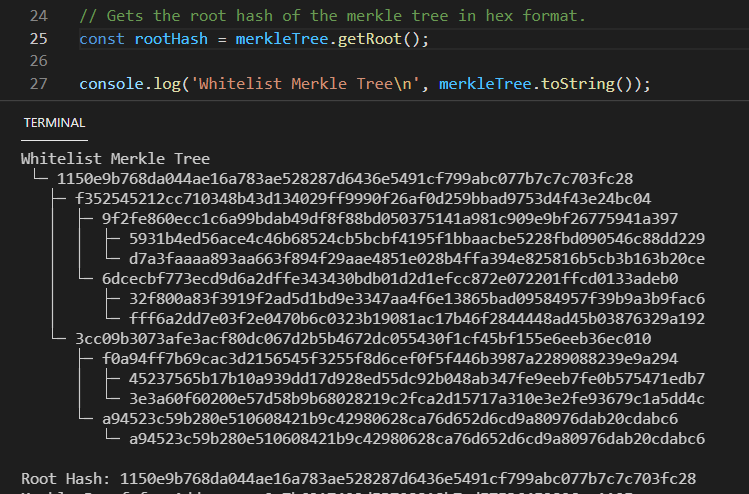
Agora que derivamos uma Merkle Tree completa, podemos obter o hash raiz chamando o método getRoot() (Figura 3) no nosso objeto Merkle Tree. Lembre-se de que o hash raiz de uma Merkle Tree é o hash dos dois nós pai anteriores diretamente sob o nó raiz na árvore. Neste caso, 0xf352... e 0x3cc0.... O console registra a nossa Merkle Tree utilizando o método toString() que fornece para nós uma boa visualização de como a nossa árvore está estruturada.
A engenhosidade de uma Merkle Tree deriva do fato de não exigir qualquer conhecimento dos blocos de dados originais para verificar que um nó pertence à nossa árvore. Se estamos tentando verificar que um nó de folha pertence à nossa árvore, só é necessário o conhecimento do hash dos nós de folha vizinhos diretos, se houver, e o nó pai vizinho mistura diretamente acima dos nós de folha. Para uma breve e doce explicação de como isso funciona, recomendo que você veja esse vídeo da Tara Vancil. Essa informação é conhecida como prova e será utilizada no nosso smart contract Solidity para verificar se um chamador está fora da nossa whitelist.
Implementação do Website
Agora que temos tanto o nosso objeto Merkle Tree como o seu hash raiz, estamos prontos para começar a pensar em como podemos fornecer uma prova Merkle ao nosso smart contract quando um usuário da whitelist tentar reivindicar seus tokens. Tudo que realmente precisa ser feito é implementar algum JavaScript, semelhante ao acima mencionado, no nosso website do projeto que faz um pedido de busca a uma API externa enquanto na página de mint. Essa API receberá o endereço das carteiras ligadas, pois foi isso que utilizámos originalmente para gerar os nossos nós de folha, e devolverá a prova designada.
Do lado do servidor, você receberia um endereço, a sua utilização de keccak256, e recuperaria a prova usando o método getHexProof() no nosso objeto Merkle Tree. A imagem abaixo (Figura 4) mostra um exemplo do que poderia retornar a partir desta chamada API.
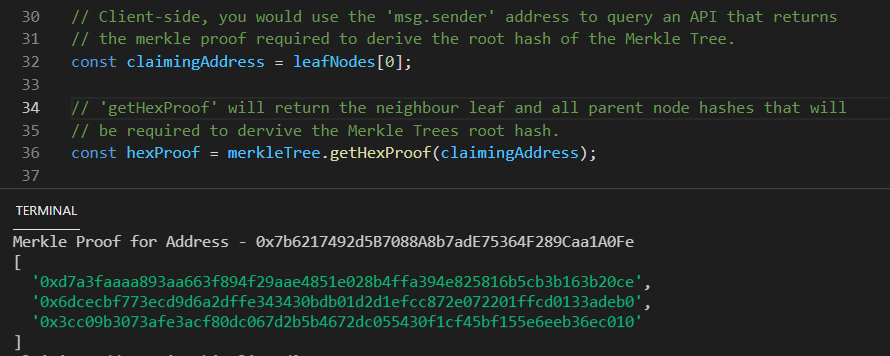
Depois desta prova ser recebida e enviada como parâmetro com a transação dos participantes, podemos agora começar a analisar a forma como nós verificamos no nosso smart contract.
Implementação do smart contract
Nota: O exemplo de smart contract apresentado foi construído com a quantidade mínima de código necessária para mostrar uma prova de conceito. Não é de forma alguma um exemplo de como se deve escrever uma função de minting.
A primeira coisa que devemos fazer para validar a prova fornecida, é importar OpenZeppelin MerkleProof.sol contract (Linha 6, Figura 5), o que nos permitirá utilizar a função MerkleProof.verify() no nosso código de smart contract. A próxima coisa necessária é definir a raiz do hash Merkle. Se o smart contract tiver sido implantado na rede principal Ethereum antes da whitelist ser finalizada, assume-se que existe alguma função de setter que pode ser utilizada para atualizar este valor num momento posterior. Neste caso, codifiquei o valor de hash de raiz Merkle para que seja definido no momento da implementação (Linha 12, Figura 5).
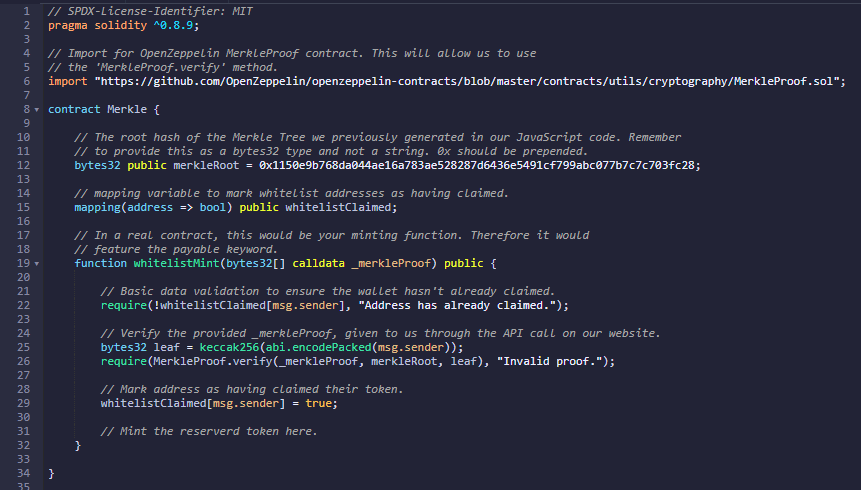
A seguir, precisamos verificar a prova. Recorde que a prova foi enviada com a transação e era um conjunto de valores do tipo bytes32. Tecnicamente eram de tipo string, mas o Solidity irá interpretá-los corretamente independentemente disso. Geramos o nosso nó de folha alvo (Linha 25, Figura 5), que, se você se lembrar, era o hash keccak256 de um endereço da whitelist. Neste exemplo, estamos gerando o nosso nó de folha alvo ao misturar o valor de msg.sender. Lembre-se de que este valor é imutável e não pode ser maliciosamente alterado.
Devido ao fato de apenas endereços não incluídos na whitelist serem utilizados para gerar os nossos nós de folha, já se pode assumir que se um endereço não incluído na whitelist tentar chamar esta função utilizando uma prova válida ou inválida, o nó de folha alvo gerado simplesmente não existirá no nosso Merkle Tree e a verificação falhará. A etapa final desta implementação chama simplesmente a função MerkleProof.verify() passando a prova fornecida como o primeiro argumento, o hash Merkle raiz como o segundo, e o nó de folha alvo como o último. Se esta função retornar false, a declaração de exigência falhará e a transação será simplesmente revertida, caso contrário, a função continuará a ser executada e os tokens serão cunhados.
Palavras de despedida
Aí está! Uma abordagem relativamente simples e direta para mostrar como a utilização das Merkle Trees para a reivindicação da whitelist num projeto NFT pode proporcionar-lhe paz de espírito de modo a que apenas endereços designados da sua whitelist sejam capazes de reivindicar. Sei que estão disponíveis outras soluções, mas das que pesquisei, esta foi de longe a mais interessante. Espero que tenham gostado tanto de ler este artigo tanto quanto eu gostei quando o pesquisei, por favor sintam-se à vontade para aplaudir e me seguir no Twitter para atualizações daquilo em que estou trabalhando e quando o meu próximo artigo for publicado. ✌️
Top comments (0)