Este artigo é o quinto de uma série de artigos sobre matemática em Solidity. Desta vez o tópico é: expoente e logaritmo.

Tradução de Mikhail Vladimirov feita por Marcelo Creimer, artigo original disponível aqui.

Introdução

Por séculos, o logaritmo foi usado para simplificar cálculos. Antes das calculadoras eletrônicas se tornarem amplamente disponíveis, a régua de cálculo, calculadora mecânica baseada em logaritmo, foi o símbolo da profissão de engenheiro.

Função logarítmica, junto com função exponencial, do qual a função logarítmica é o seu inverso, permite transformar multiplicação em adição e, o que é ainda mais importante, exponenciação em multiplicação. Isto é possível devido às seguintes duas regras:

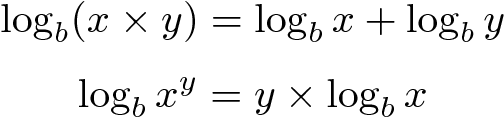
Depois exponenciar as partes esquerda e direita destas equações, nós temos:

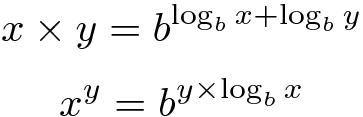
Note que estas fórmulas também funcionam para positivos arbitrários base b diferentes dessa, portanto nós podemos escolher a base que seja conveniente para implementação.

Neste artigo nós iremos mostrar como as funções logarítmica e exponencial base 2 podem ser eficientemente implementadas em Solidity, como estas funções base 2 podem ser convertidas nas correspondentes funções naturais (base e), e quais são os casos de uso reais para estas funções em aplicações DeFi.

Portanto o foco deste artigo é expoente e logaritmo.

Logaritmo

Vamos começar com logaritmo binário (base 2). Logaritmo binário de x, é o valor y de modo que:

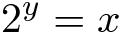
Obviamente, o valor de x tem de ser positivo para y existir.

Note que se

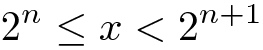
então

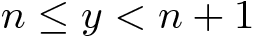
portanto n é a parte inteira do logaritmo binário de x. Desse modo, nossa primeira questão é:

Como Calcular a Parte Inteira de Logaritmo Binário em Solidity?

Spoiler: dê um shift right e conte.

Aqui está uma abordagem direta que funciona para o inteiro positivo x:

for (n = 0; x > 1; x >>= 1) n += 1;

Enquanto é claro e simples, este método é bastante caro já que seu consumo de gas é O(n). Aqui está a versão aprimorada que funciona para inteiro positivo 256-bit x:

if (x >= 2**128) { x >>= 128; n += 128; }
if (x >= 2**64) { x >>= 64; n += 64; }
if (x >= 2**32) { x >>= 32; n += 32; }
if (x >= 2**16) { x >>= 16; n += 16; }
if (x >= 2**8) { x >>= 8; n += 8; }
if (x >= 2**4) { x >>= 4; n += 4; }
if (x >= 2**2) { x >>= 2; n += 2; }
if (x >= 2**1) { /* x >>= 1; */ n += 1; 

Esta implementação aprimorada consome cerca de 600 gas no pior caso: 25 vezes menos que a original, não-otimizada.

Por enquanto tudo bem, mas

E se X for Fracionário?

Spoiler: basta adicionar expoente.

Não há números fracionários no núcleo da linguagem Solidity, mas há muitas maneiras destes números serem emulados. Vamos considerar duas destas maneiras: binário fixo e binário de ponto-flutuante. Ambas as maneiras representam número fracionário x como este:

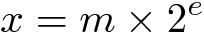
onde m e e são inteiros. O valor m é conhecido como mantissa e e é conhecido como expoente. A diferença entre binário fixo e números de ponto-flutuante é que para número de ponto-fixo expoente é uma constante pré-definida, geralmente negativa, assim somente a mantissa tem de ser armazenada; enquanto para número de ponto-flutuante expoente é variável e assim, ele tem de ser armazenado junto com a mantissa.

Agora vamos reparar que:

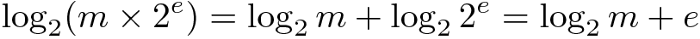
Então, o logaritmo binário de um número binário fixo ou de ponto-flutuante poderia ser calculado como logaritmo binário da mantissa, mais expoente. Enquanto o expoente for inteiro, a mesma fórmula também funciona para a parte inteira do logaritmo.

Agora, que nós sabemos como acumular a parte inteira,

E Sobre a Parte Fracionária do Logaritmo Binário de A?

Spoiler: quadrado e metade.

Considere n a parte inteira do logaritmo binário de x, então a parte fracionária do logaritmo pode ser calculada assim:

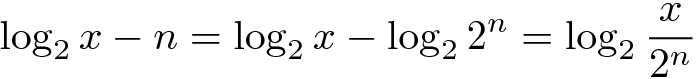
Note que enquanto

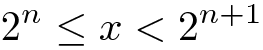
então

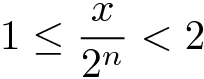
Portanto, calcular a parte fracional de um logaritmo binário poderia ser deduzido do cálculo do logaritmo binário de um número entre 1 (inclusive) e 2 (exclusive). Para fazer esse cálculo nós usaremos as seguintes duas regras:

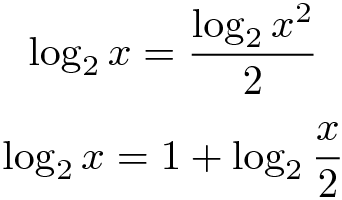
Aqui está o código escrito como se o Solidity suportasse nativamente números fracionais:

for (delta = 1; delta >= precisão; delta /= 2) {
   if (x >= 2) { resultado += delta; x /= 2; }
   x *= x;
}

A cada iteração, nós aplicamos a regra antiga: eleve ao quadrado o valor de x e reduza à metade o valor de delta. Se em algum ponto o valor de x se tornar maior que ou igual a 2, então nós aplicamos a última regra: adicionar delta ao resultado e dividir por 2 o valor de x. Nós repetimos o loop até delta cair abaixo da desejada precisão já que continuando com os cálculos não adicionaria nada significante ao resultado.

Infelizmente,o Solidity não suporta frações nativamente, então o código real se pareceria com algo assim:

for (delta = ONE;
    gte (delta, precisão);
    delta = div (delta, TWO)) {
 if (gte (x, TWO)) {
   result = add (resultado, delta);
   x = div (x, TWO);
 }
 x = mul (x, x);
}

onde ONE, TWO, add, mul, div, e gte são constantes e funções emulando alguns tipos de números fracionários e aritméticos neles em Solidity.

Felizmente, a biblioteca ABDK Libraries tem pronta para uso a implementação do logaritmo binário para 64.64-bit para binário de ponto-fixo, quádrupla precisão e números binários de ponto-flutuante.

Agora que nós sabemos como calcular logaritmo de número binário,

E os Logaritmos Natural e Comum?

Spoiler: fatores mágicos.

Para calcularmos logaritmos natural (base e) e comum (base 10), nós podemos usar a seguinte regra:

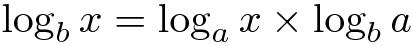
assim,

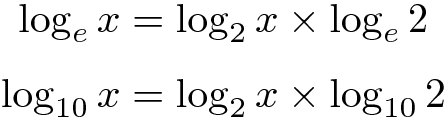
Aqui

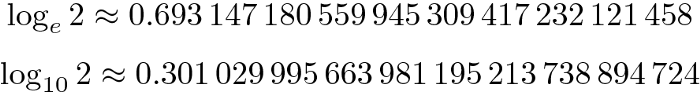
são fatores mágicos que podem ser escritos no código (hardcoded) e não precisam ser calculados em tempo de execução (runtime).

Agora que já acabamos com logaritmo, vamos mudar para

Expoente

Novamente, vamos começar com exponenciação base 2, ou seja, calculando

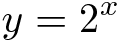
Solidity tem o operador ** para potência, então a solução óbvia seria:

y = 2**x

Entretanto, isto funciona somente para aqueles valores de x, que são simultaneamente inteiros e não-negativos. Além disso, este modo não é o mais eficiente, já que usando a operação shift seria um pouco mais barato:

y = 1 << x

O shift pode também ajudar com valores negativos de x:

y = x >= 0 ? 1 << x : 1 >> -x

Como o Solidity não suporta frações nativamente, qualquer x negativo irá levar a zero como resultado, o que não faz muito sentido. Entretanto, se nós substituíssemos o inteiro 1 aqui com a representação de ponto-fixo de 1, este código se tornaria mais razoável.

É até mais simples para números binários de ponto-flutuante, já que na fórmula acima, y é o número binário de ponto-flutuante com mantissa igual a 1 e expoente igual a x.

Por enquanto tudo bem, mas

E se X for Fracionário?

Spoiler: multiplique fatores mágicos.

Vamos dividir um valor fracionário de x na parte inteira n e a parte fracional f:

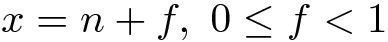
então

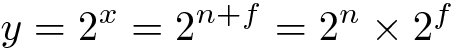
Consideremos f ser uma fração binária:

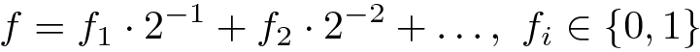
então

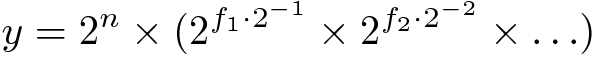
Note que:

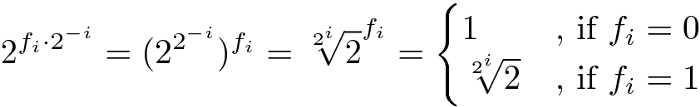
Os fatores mágicos,

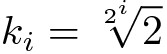
Poderiam ser pré-computados e não precisam ser calculados em tempo de execução:

Isto é bom, mas

Quantos Fatores Mágicos Deveríamos Pré-Computar?

Spoiler: tantos quanto os desejados bits de precisão.

Para números binários ponto-fixo, a resposta é óbvia, já que o número de dígitos binários depois do ponto é fixo. Portanto, se o ponto fixo tem 64 bits na parte fracional, então nós precisamos de 64 fatores mágicos.

Para números binários de ponto-flutuante as coisas são um pouco mais complicadas, já que a mantissa m poderia sofrer um grande shift para a direita pelo largo expoente negativo e. Então, a representação binária deste número de ponto-flutuante pareceria com isto:

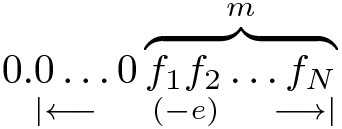
Felizmente, para qualquer f entre 0 e 1, é verdadeiro que

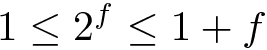
de modo que se f é o número cuja representação binária foi mostrada acima, então

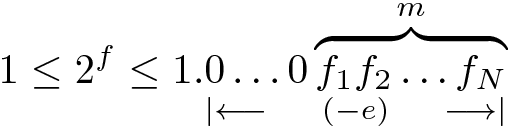
Assim, se a precisão do resultado esperado é M bits, então nós podemos apenas ignorar estes bits da representação binária de f, que estão localizados mais para frente que M casas binárias após o ponto. Deste modo nós precisaríamos no máximo M fatores mágicos pré-computados para calcular o expoente.

Implementações de funções exponenciais base 2 para números binário fixo e ponto-flutuante prontas para usar podem ser encontradas no código fonte da biblioteca ABDK Libraries.

Exponencial base 2 é bom, mas

E Exponencial com Base Arbitrária?

Spoiler: use logaritmo.

Nós sabemos, que para x positivo arbitrário e positivo arbitrário b que não seja um, o seguinte é verdade:

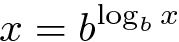
Então, para um arbitrário y:

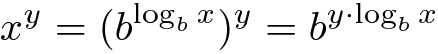
Para b=2 isto nos dá:

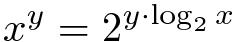
Como nós já sabemos como calcular as funções logaritmo base-2 e exponencial, nós podemos calcular funções exponenciais com base arbitrária.

Esta fórmula pode ser usada para efetivamente calcular juros compostos contínuos:

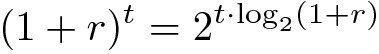
Aqui r é a taxa de juros para uma única unidade de tempo e t é o tamanho do intervalo de tempo para o qual se quer calcular juros compostos. Note que no caso de uma taxa de juros fixa, o valor

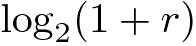
poderia ser calculado somente uma vez, provavelmente off-chain, e então reusado, o que poderia fazer esta fórmula até mesmo mais eficiente.

Conclusão

Neste artigo nós mostramos como as funções logaritmo base-2 e exponencial poderiam ser eficientemente calculadas em Solidity para números binários de ponto fixo e flutuante.

Nós também descrevemos, como funções logarítmicas de base arbitrária e exponencial podem ser implementadas via funções base-2.

Nós apresentamos um caso de uso real de cálculo de taxa de juros compostas contínua eficientemente implementadas usando funções logarítmicas e exponenciais.

No nosso próximo artigo nós iremos mostrar mais casos de uso para logaritmo e expoente em aplicações DeFi, o próximo tópico será: Bancor formula.

Outros artigos desta série:

· Parte 1: Números
· Parte 2: Overflow
· Parte 3: Porcentagens e Proporções
· Parte 4: Juros Compostos