Mistérios das Redes Neurais Parte V

A condução autônoma, a área da saúde ou o varejo são apenas algumas das áreas em que a Visão Computacional nos permitiu alcançar coisas que, até recentemente, eram consideradas impossíveis. Hoje, o sonho de um carro autônomo ou uma mercearia automatizada não parece mais tão futurista. Na verdade, estamos usando a Visão Computacional todos os dias — quando desbloqueamos o telefone com nosso rosto ou retocamos fotos automaticamente antes de postá-las nas redes sociais. As Redes Neurais Convolucionais são possivelmente os blocos de construção mais cruciais por trás desses enormes sucessos. Desta vez, vamos ampliar nossa compreensão de como as redes neurais funcionam com ideias específicas para CNNs (Redes Neurais Convolucionais). Esteja ciente de que o artigo incluirá equações matemáticas bastante complexas, mas não se desenime se você não se sentir confortável com álgebra linear e cálculo diferencial. Meu objetivo não é fazer você lembrar dessas fórmulas, mas fornecer a intuição do que está acontecendo por baixo delas.
Notas adicionais: pela primeira vez, decidi enriquecer meu trabalho artístico com uma versão em áudio e gentilmente convido você a ouvi-la. Você encontrará um link para o Soundcloud acima. Neste artigo, foco principalmente em coisas típicas das CNNs. Se você estiver procurando informações mais gerais sobre redes neurais profundas, recomendo que você leia meus outros posts desta série. Como de costume, o código-fonte completo, com visualizações e comentários, pode ser encontrado no meu GitHub. Vamos começar!
Introdução
No passado, conhecemos as chamadas redes neurais densamente conectadas. Essas são redes cujos neurônios são divididos em grupos formando camadas sucessivas. Cada unidade desse tipo está conectada a cada único neurônio das camadas vizinhas. Um exemplo de tal arquitetura é mostrado na figura abaixo.
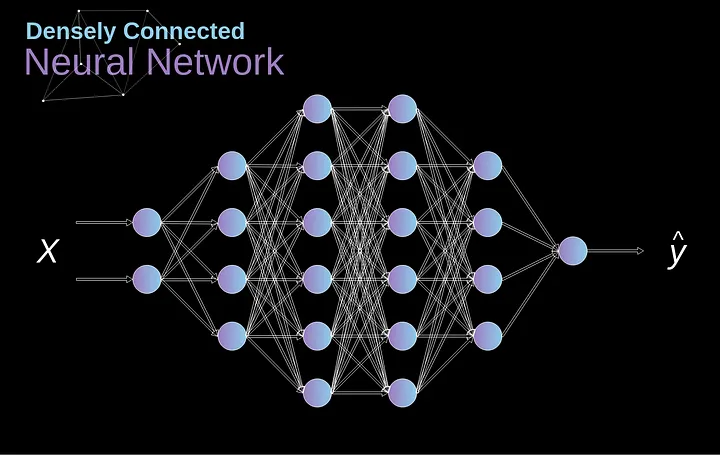 ######Figura 1. Arquitetura da rede neural densamente conectada
######Figura 1. Arquitetura da rede neural densamente conectada
Essa abordagem funciona bem quando resolvemos problemas de classificação com base em um conjunto limitado de características definidas — por exemplo, prever a posição de um jogador de futebol com base nas estatísticas que ele registra durante os jogos. No entanto, a situação se torna mais complicada ao trabalhar com fotos. Claro, poderíamos tratar o brilho de cada pixel como uma característica separada e passá-lo como entrada para nossa rede densa. Infelizmente, para que funcione para uma foto típica de smartphone, nossa rede teria que conter dezenas ou até centenas de milhões de neurônios. Por outro lado, poderíamos redimensionar nossa foto, mas perderíamos informações valiosas no processo. Imediatamente percebemos que uma estratégia tradicional não nos ajuda em nada — precisamos de uma nova maneira inteligente de usar o máximo de dados possível, mas ao mesmo tempo reduzir o número de cálculos e parâmetros necessários. É aí que as CNNs entram em jogo.
Estrutura de dados de fotos digitais
Vamos começar explicando como as imagens digitais são armazenadas. A maioria de vocês provavelmente percebe que elas são, na verdade, enormes matrizes de números. Cada número corresponde ao brilho de um único pixel. No modelo RGB (Red (vermelho), Green (verde) e Blue (azul)), a imagem colorida é composta por três dessas matrizes correspondentes a três canais de cor — vermelho, verde e azul. Em imagens em preto e branco, só precisamos de uma matriz. Cada uma dessas matrizes armazena valores de 0 a 255. Essa faixa é um compromisso entre a eficácia de armazenar informações sobre a imagem (256 valores se encaixam perfeitamente em 1 byte) e a sensibilidade do olho humano (distinguimos um número limitado de tons da mesma cor).
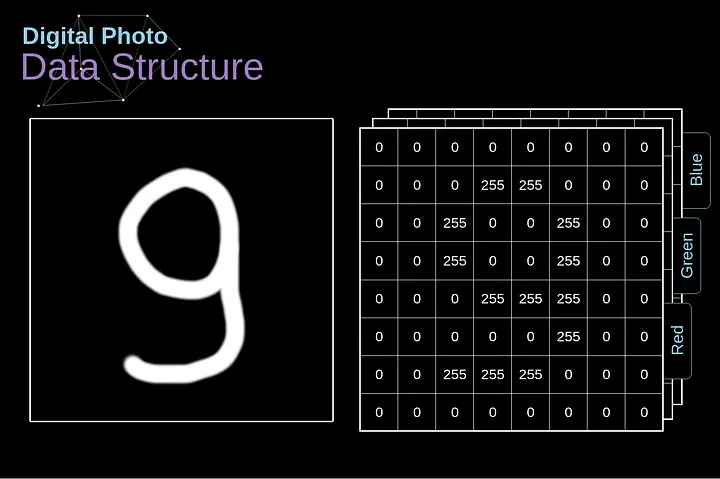 ######Figura 2. Estrutura de dados por trás de imagens digitais
######Figura 2. Estrutura de dados por trás de imagens digitais
Convolução
A convolução do kernel é utilizada não apenas em CNNs, mas também é um elemento-chave em muitos outros algoritmos de Visão Computacional. É um processo no qual tomamos uma pequena matriz de números (chamada de kernel ou filtro), passamos sobre nossa imagem e a transformamos com base nos valores do filtro. Os valores subsequentes do mapa de características são calculados de acordo com a seguinte fórmula, onde a imagem de entrada é denotada por f e nosso kernel por h. Os índices das linhas e colunas da matriz resultante são marcados com m e n, respectivamente.
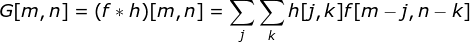
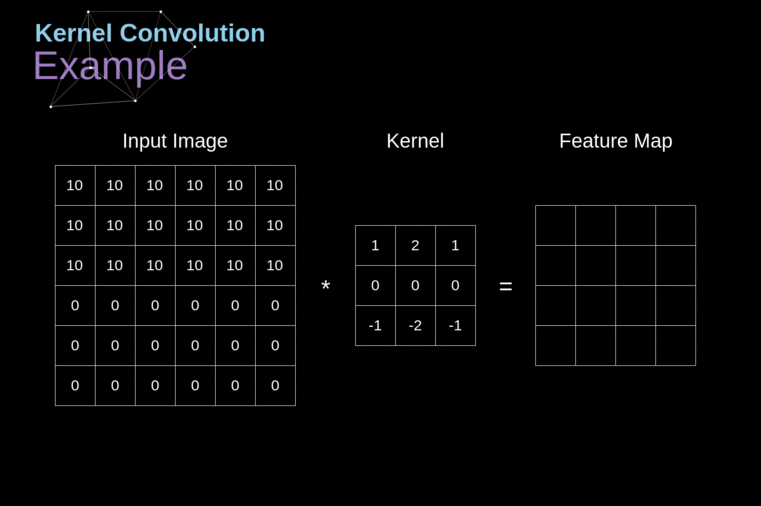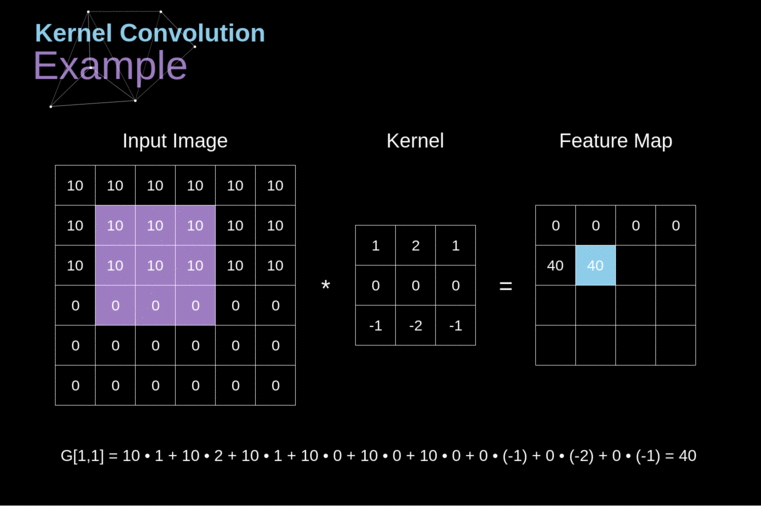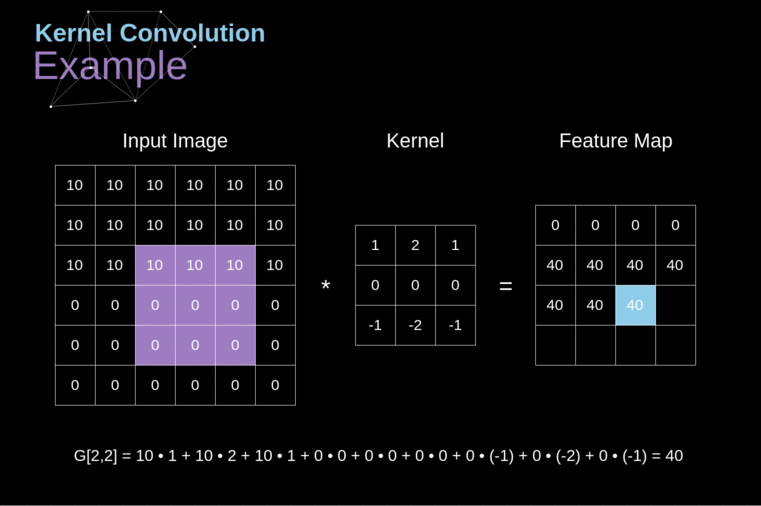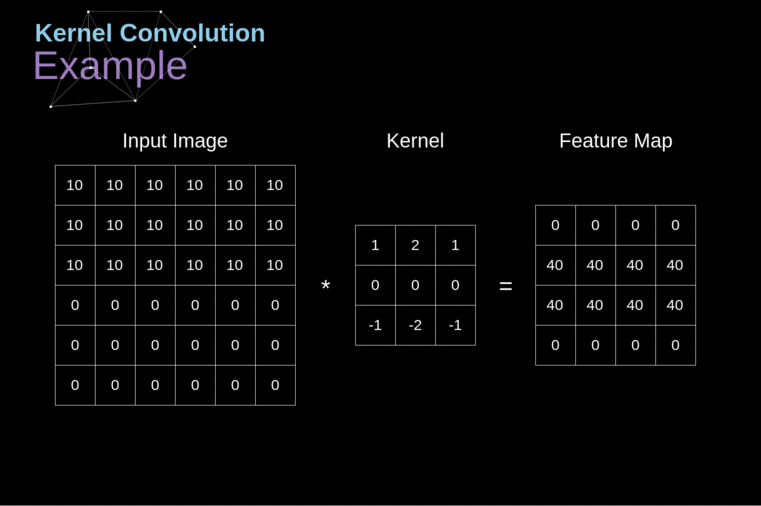 ######Figura 3. Exemplo de Convolução do Kernel
######Figura 3. Exemplo de Convolução do Kernel
Após posicionar nosso filtro sobre um pixel selecionado, pegamos cada valor do kernel e os multiplicamos em pares com os valores correspondentes da imagem. Finalmente, somamos tudo e colocamos o resultado no local correto no mapa de características de saída. Acima, podemos ver como essa operação se parece em uma escala micro, mas o que é ainda mais interessante é o que podemos alcançar ao realizá-la em uma imagem completa. A Figura 4 mostra os resultados da convolução com vários filtros diferentes.
 ######Figura 4. Encontrando bordas com convolução do kernel [Imagem Original]
######Figura 4. Encontrando bordas com convolução do kernel [Imagem Original]
Convolução Válida e Idêntica
Como vimos na Figura 3, quando realizamos a convolução sobre a imagem de 6x6 com um kernel de 3x3, obtemos um mapa de características de 4x4. Isso ocorre porque existem apenas 16 posições únicas onde podemos colocar nosso filtro dentro desta imagem. Como nossa imagem diminui a cada vez que realizamos a convolução, podemos fazê-lo apenas um número limitado de vezes, antes que nossa imagem desapareça completamente. Além disso, se observarmos como nosso kernel se move pela imagem, veremos que o impacto dos pixels localizados nas bordas é muito menor do que aqueles no centro da imagem. Dessa forma, perdemos parte das informações contidas na imagem. Abaixo, você pode ver como a posição do pixel altera sua influência no mapa de características.
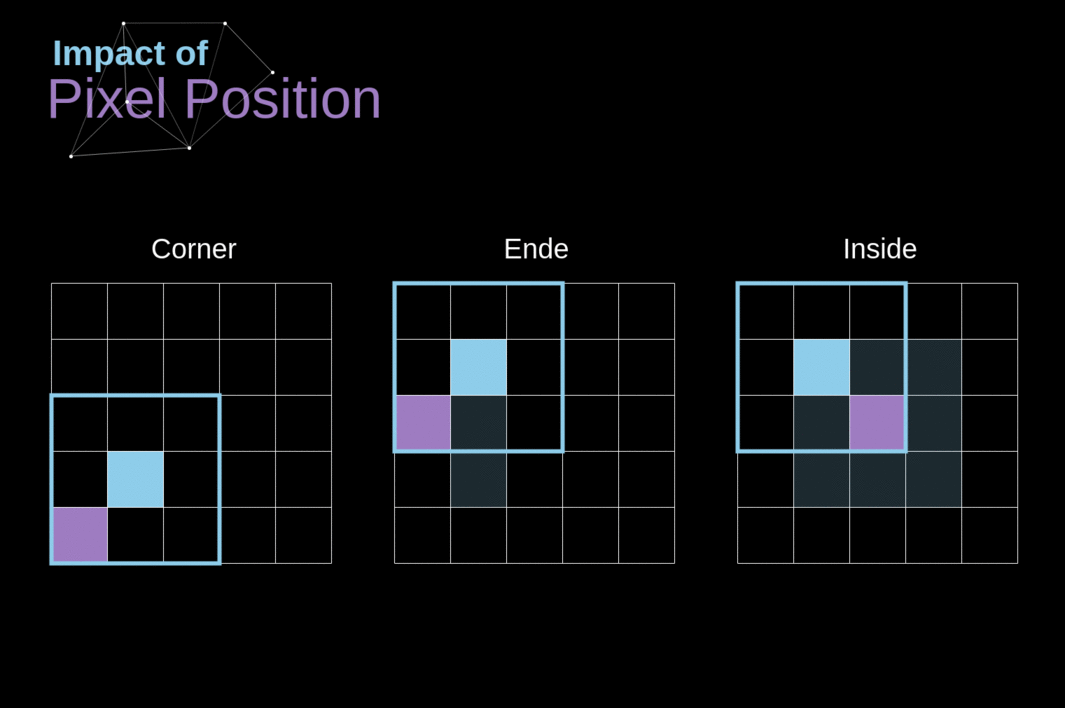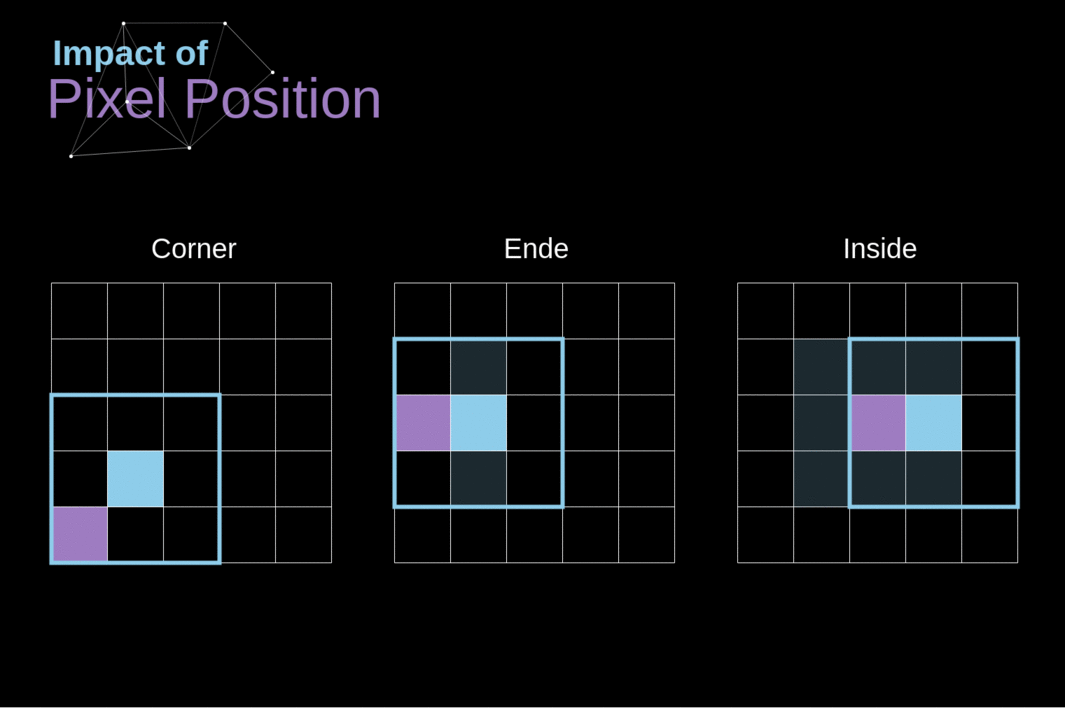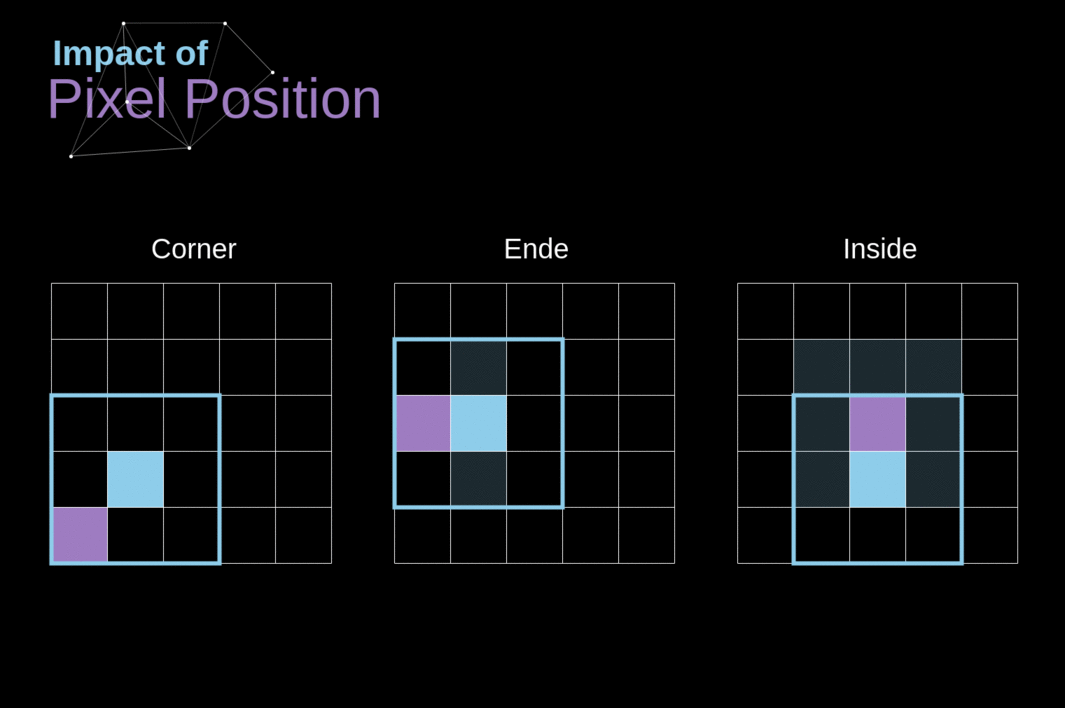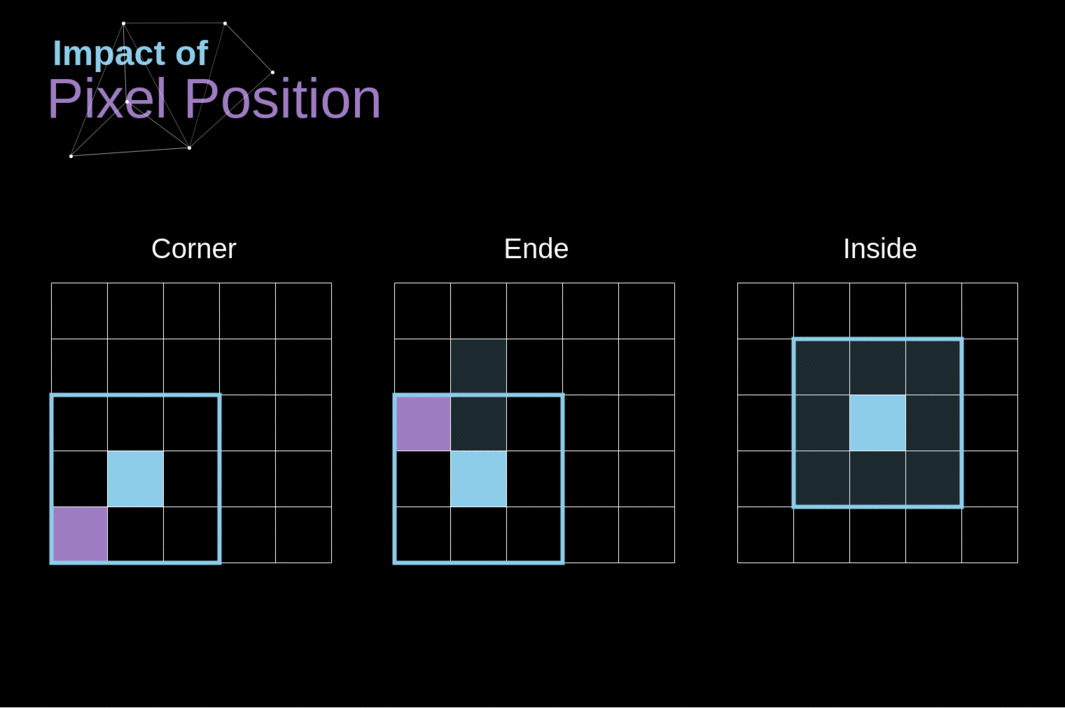 ######Figura 5. Impacto da posição do pixel
######Figura 5. Impacto da posição do pixel
Para resolver ambos esses problemas, podemos adicionar uma borda à nossa imagem. Por exemplo, se usarmos um preenchimento de 1 pixel, aumentamos o tamanho da nossa foto para 8x8, de modo que a saída da convolução com o filtro de 3x3 será 6x6. Geralmente, na prática, preenchemos a borda adicional com zeros. Dependendo se usamos preenchimento ou não, lidamos com dois tipos de convolução - Válida e idêntica. A nomenclatura é um pouco ruim, então, para maior clareza: Válida - significa que usamos a imagem original; Idêntica - usamos a borda ao redor dela, de modo que as imagens na entrada e saída tenham o mesmo tamanho. No segundo caso, a largura do preenchimento deve obedecer à seguinte equação, onde p é o preenchimento e f é a dimensão do filtro (geralmente ímpar).
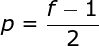
Convolução com Deslocamento (Strided Convolution)
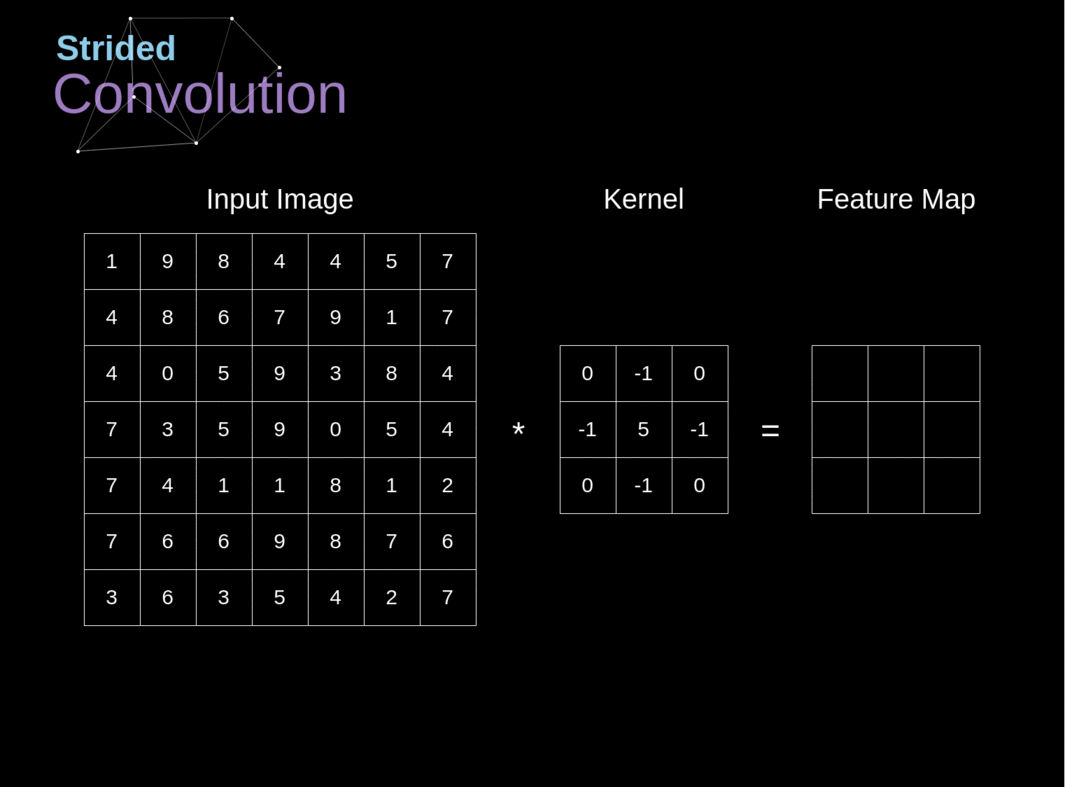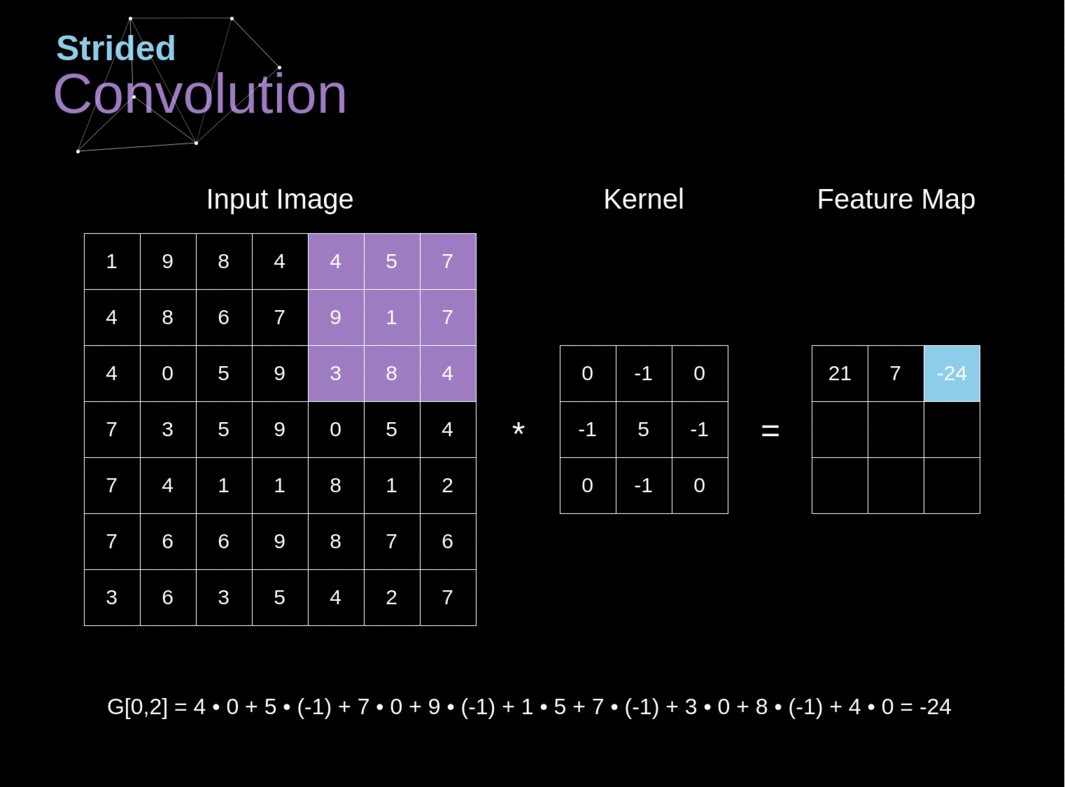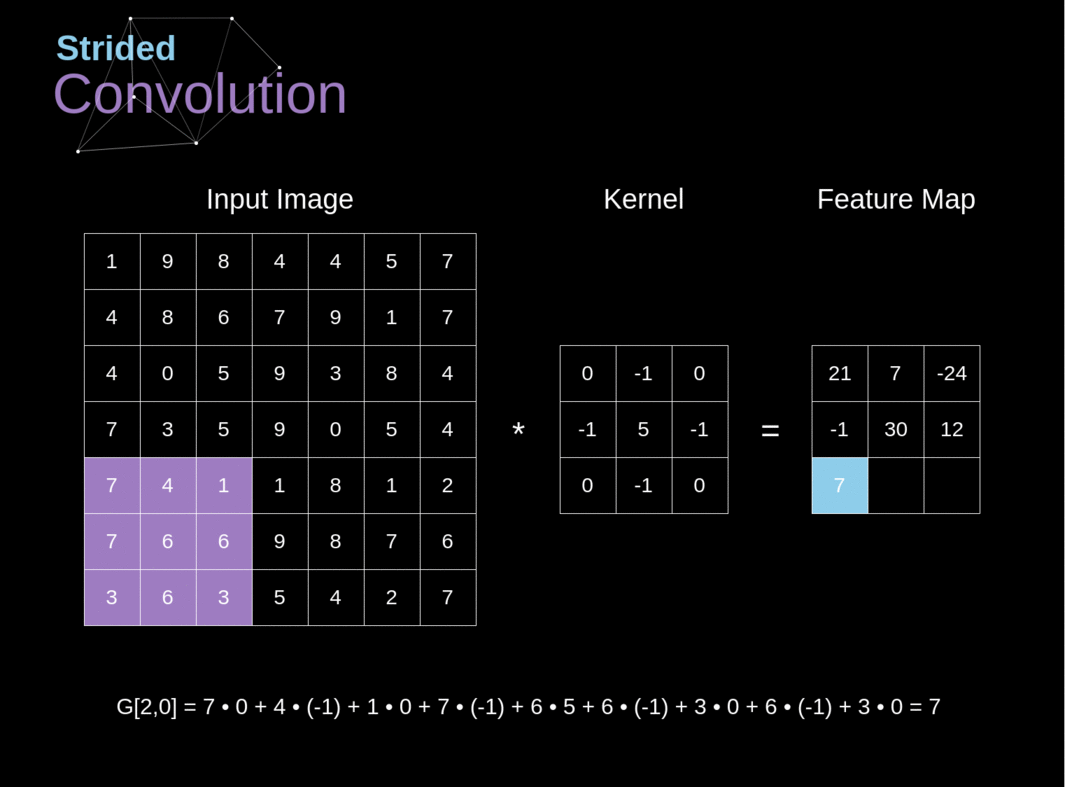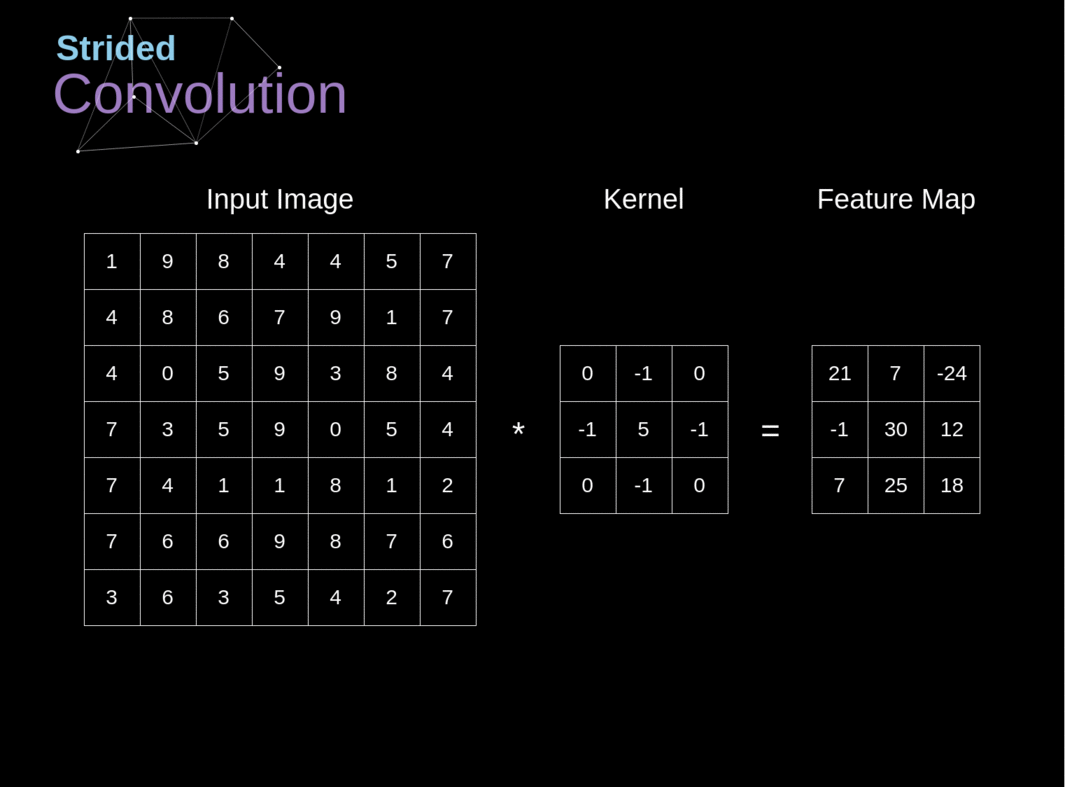 ######Figura 6. Exemplo de convolução com deslocamento
######Figura 6. Exemplo de convolução com deslocamento
Nos exemplos anteriores, sempre deslocamos nosso kernel por um pixel. No entanto, o comprimento do passo também pode ser tratado como um dos hiperparâmetros da camada de convolução. Na Figura 6, podemos ver como a convolução se parece quando usamos um passo maior. Ao projetar nossa arquitetura de CNN, podemos decidir aumentar o passo se quisermos que os campos receptivos se sobreponham menos ou se quisermos dimensões espaciais menores em nosso mapa de características. As dimensões da matriz de saída - levando em consideração o preenchimento e o deslocamento - podem ser calculadas usando a seguinte fórmula.
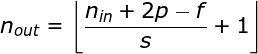
A transição para a terceira dimensão
A convolução sobre o volume é um conceito muito importante, que nos permitirá não apenas trabalhar com imagens coloridas, mas, ainda mais importante, aplicar vários filtros dentro de uma única camada. A primeira regra importante é que o filtro e a imagem na qual você deseja aplicá-lo devem ter o mesmo número de canais. Basicamente, procedemos de maneira muito semelhante ao exemplo da Figura 3; no entanto, desta vez multiplicamos os pares de valores do espaço tridimensional. Se quisermos usar vários filtros na mesma imagem, realizamos a convolução de cada um deles separadamente, empilhamos os resultados um sobre o outro e os combinamos como um todo. As dimensões do tensor recebido (como nossa matriz 3D pode ser chamada) obedecem à seguinte equação, na qual: n - tamanho da imagem, f - tamanho do filtro, nc - número de canais na imagem, p - preenchimento usado, s - passo usado, nf - número de filtros.
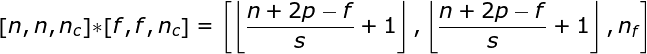
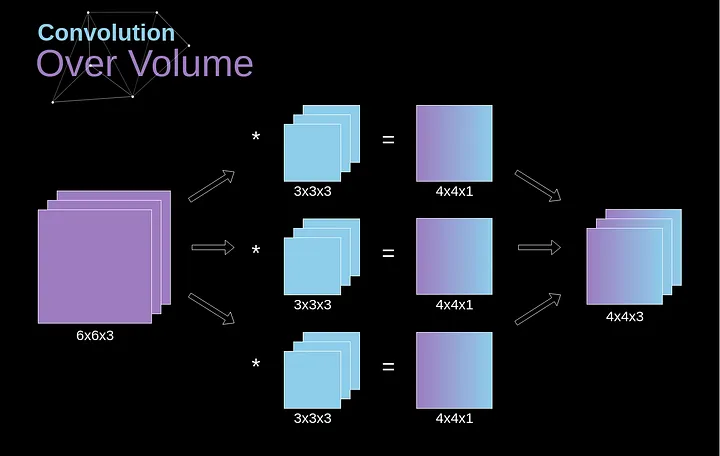 ######Figura 7. Convolução sobre volume
######Figura 7. Convolução sobre volume
Camadas de Convolução
Chegou finalmente o momento de usar tudo o que aprendemos hoje e construir uma única camada de nossa CNN. Nossa metodologia é quase idêntica àquela que usamos para redes neurais densamente conectadas, a única diferença é que, em vez de usar uma simples multiplicação de matrizes, desta vez usaremos a convolução. A propagação para frente consiste em duas etapas. A primeira é calcular o valor intermediário Z, que é obtido como resultado da convolução dos dados de entrada da camada anterior com o tensor W (contendo os filtros), e então adicionar o viés b. A segunda etapa é a aplicação de uma função de ativação não linear ao nosso valor intermediário (nossa ativação é denotada por g). Os entusiastas de equações matriciais encontrarão fórmulas matemáticas apropriadas abaixo. Se alguma das operações em questão não estiver clara para você, recomendo muito meu artigo anterior, no qual discuto detalhadamente o que está acontecendo dentro das redes neurais densamente conectadas. Aliás, na ilustração abaixo, você pode ver uma pequena visualização descrevendo as dimensões dos tensores usados na equação.
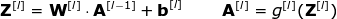
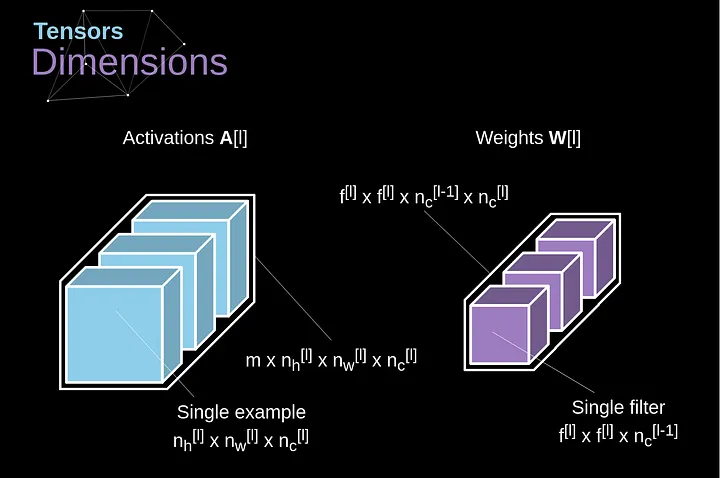 ######Figura 8. Dimensões dos Tensores
######Figura 8. Dimensões dos Tensores
Corte de Conexões e Compartilhamento de Parâmetros
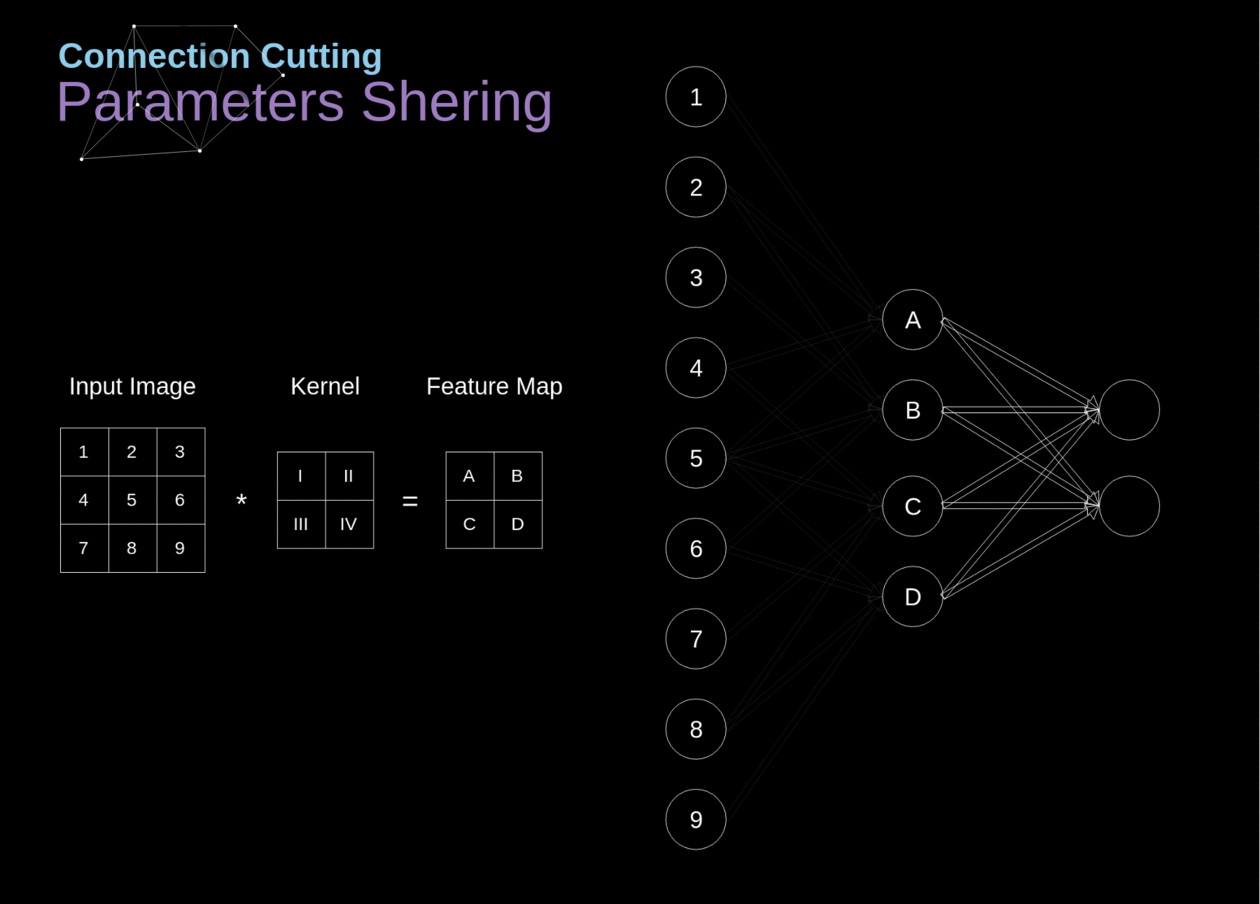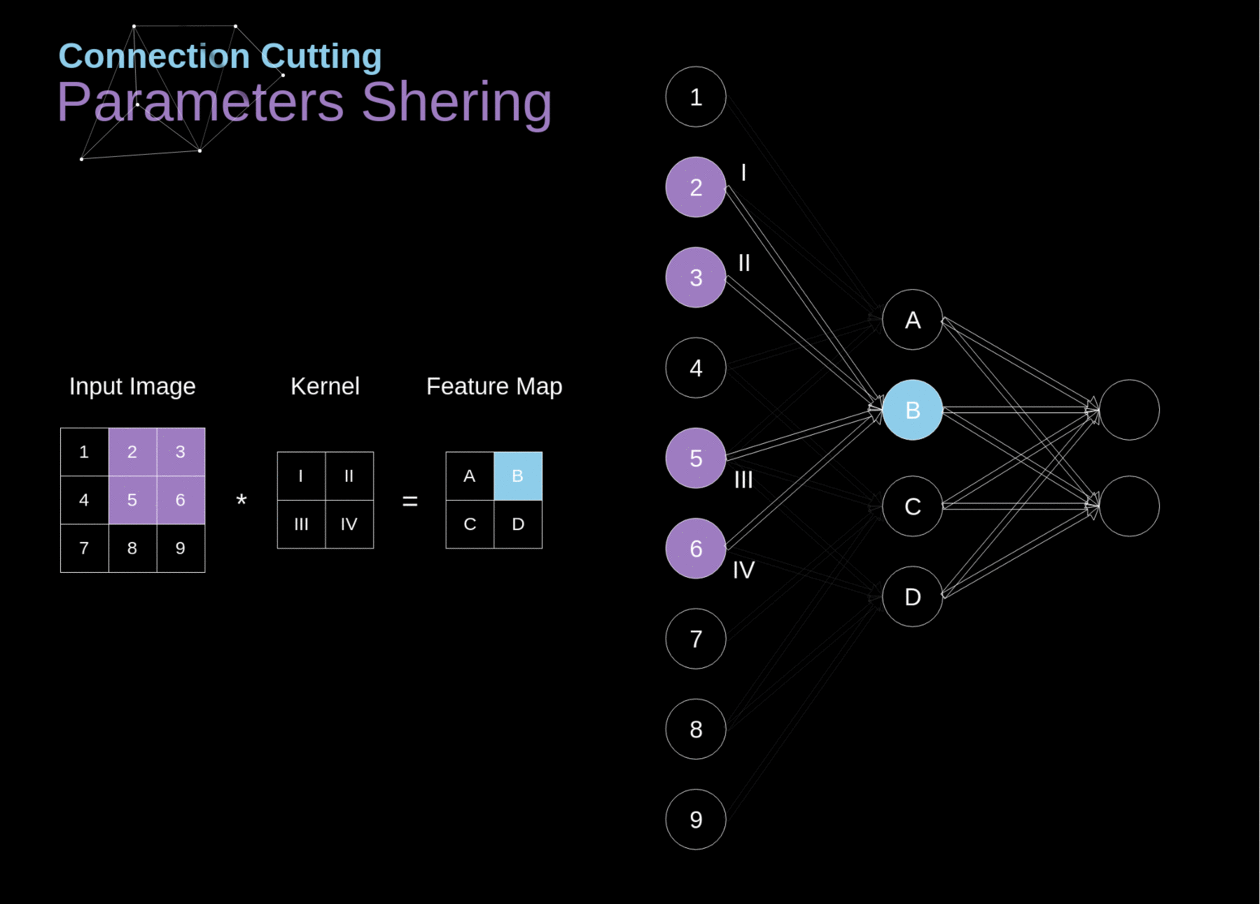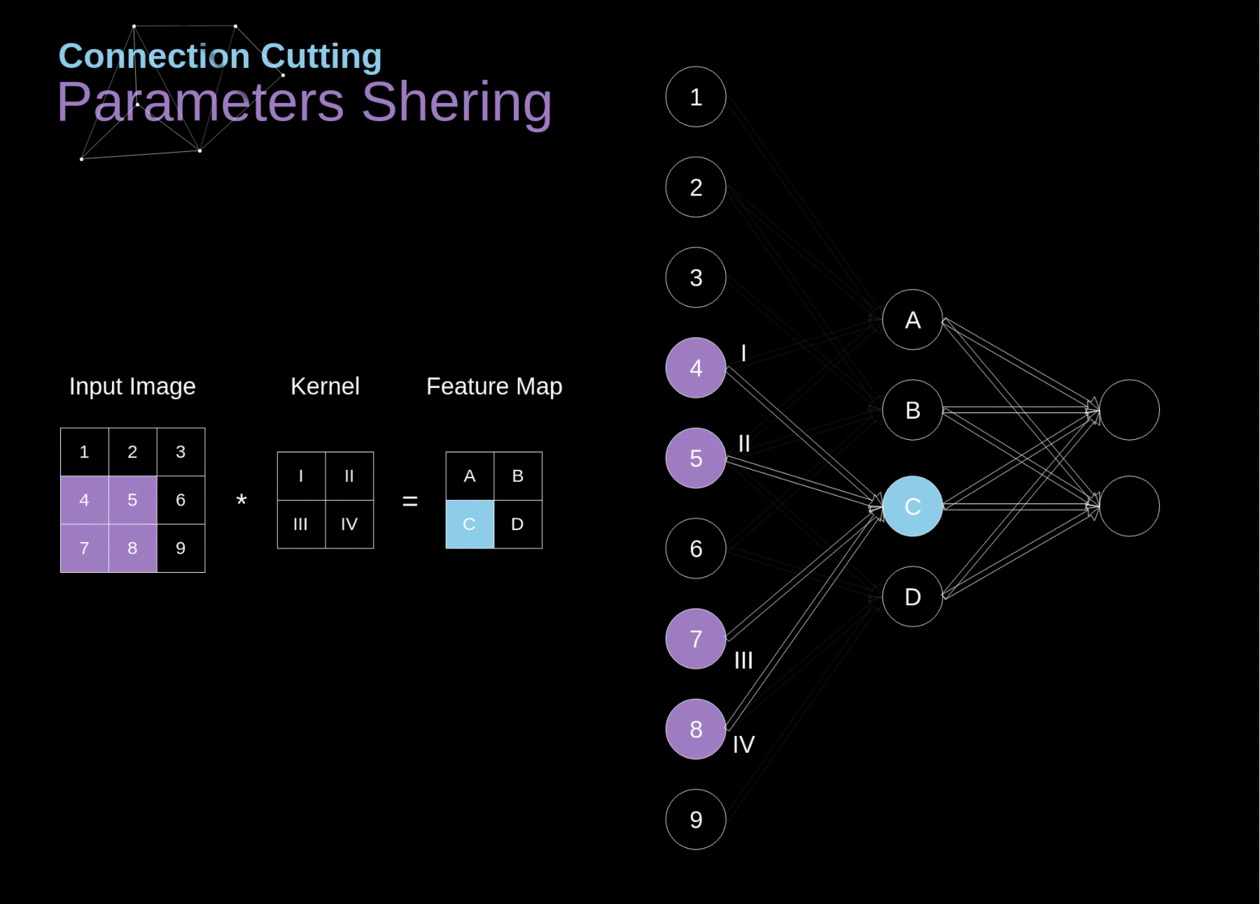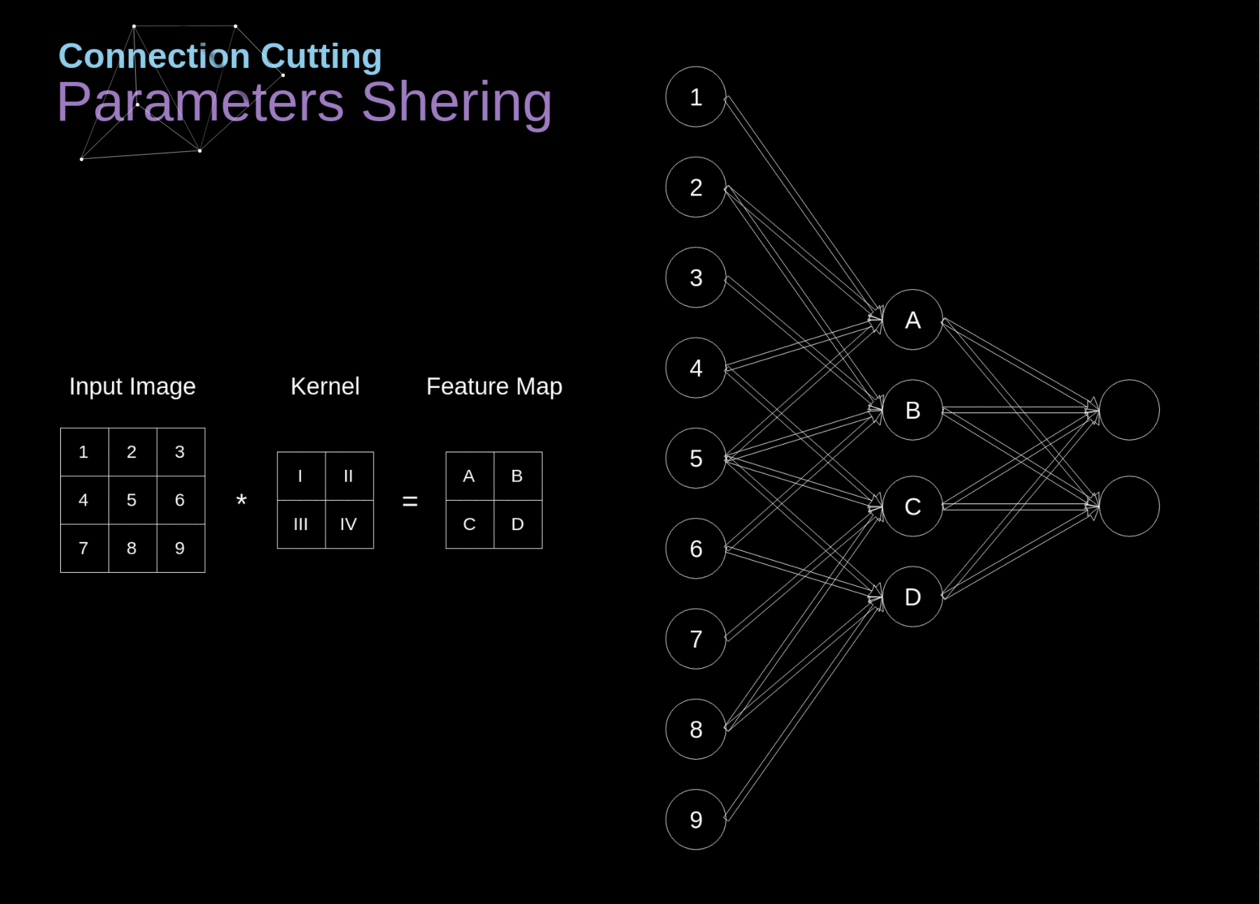
No início do artigo, mencionei que as redes neurais densamente conectadas têm dificuldade em trabalhar com imagens, devido ao grande número de parâmetros que precisariam ser aprendidos. Agora que entendemos do que se trata a convolução, vamos considerar como ela nos permite otimizar os cálculos. Na figura abaixo, a convolução 2D foi visualizada de uma maneira um pouco diferente - neurônios marcados com números de 1 a 9 formam a camada de entrada que recebe o brilho dos pixels subsequentes, enquanto as unidades A-D denotam elementos do mapa de características calculados. Por último, mas não menos importante, I-IV são os valores subsequentes do kernel - esses devem ser aprendidos.
 ######Figura 9. Corte de conexões e compartilhamento de parâmetros
######Figura 9. Corte de conexões e compartilhamento de parâmetros
Agora, vamos nos concentrar em dois atributos muito importantes das camadas de convolução. Primeiro, você pode ver que nem todos os neurônios nas duas camadas consecutivas estão conectados entre si. Por exemplo, a unidade 1 afeta apenas o valor de A. Em segundo lugar, vemos que alguns neurônios compartilham os mesmos pesos. Ambas essas propriedades significam que temos muito menos parâmetros para aprender. A propósito, vale ressaltar que um único valor do filtro afeta cada elemento do mapa de características - isso será crucial no contexto da retropropagação.
Retropropagação na Camada de Convolução
Qualquer pessoa que já tentou programar sua própria rede neural do zero sabe que a propagação para frente é apenas metade do caminho para o sucesso. A diversão real começa quando você quer retroceder. Hoje em dia, não precisamos nos preocupar com a retropropagação - os frameworks de aprendizado profundo fazem isso por nós, mas acho que vale a pena saber o que está acontecendo por baixo dos panos. Assim como nas redes neurais densamente conectadas, nosso objetivo é calcular derivadas e usá-las posteriormente para atualizar os valores de nossos parâmetros em um processo chamado descida do gradiente.
Em nossos cálculos, usaremos a regra da cadeia - que mencionei em artigos anteriores. Queremos avaliar a influência da mudança nos parâmetros no mapa de características resultante e, posteriormente, no resultado final. Antes de começarmos a entrar nos detalhes, vamos concordar com a notação matemática que usaremos - para facilitar minha vida, vou abandonar a notação completa da derivada parcial em favor da versão abreviada visível abaixo. Mas lembre-se de que, quando eu usar essa notação, sempre me referirei à derivada parcial da função de custo.
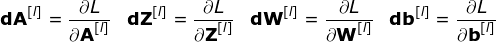
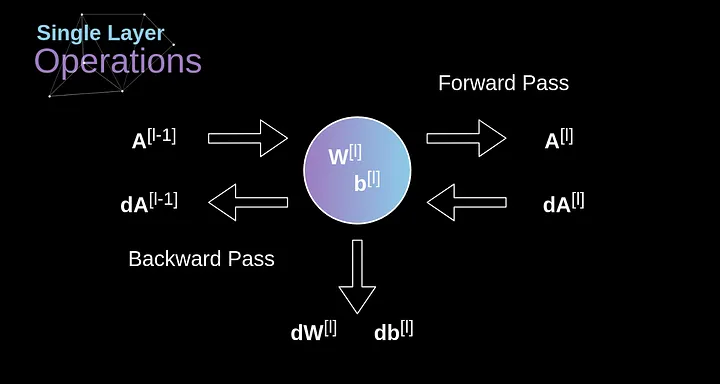 ######Figura 10. Dados de entrada e saída para uma única camada de convolução na propagação para frente e para trás
######Figura 10. Dados de entrada e saída para uma única camada de convolução na propagação para frente e para trás
Nossa tarefa é calcular dW[l] e db[l] - que são derivadas associadas aos parâmetros da camada atual, bem como o valor de dA[l -1] - que será passado para a camada anterior. Como mostrado na Figura 10, recebemos dA[l] como entrada. Obviamente, as dimensões dos tensores dW e W, db e b, assim como dA e A, respectivamente, são iguais. O primeiro passo é obter o valor intermediário dZ[l] aplicando a derivada de nossa função de ativação ao nosso tensor de entrada. De acordo com a regra da cadeia, o resultado dessa operação será usado posteriormente.
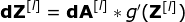
Agora, precisamos lidar com a propagação para trás da própria convolução e, para atingir esse objetivo, utilizaremos uma operação de matriz chamada convolução completa - que é visualizada abaixo. Observe que durante esse processo usamos o kernel, que foi previamente girado 180 graus. Essa operação pode ser descrita pela seguinte fórmula, onde o filtro é denotado por W, e dZ[m,n] é um escalar que pertence a uma derivada parcial obtida da camada anterior.
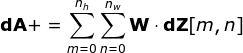
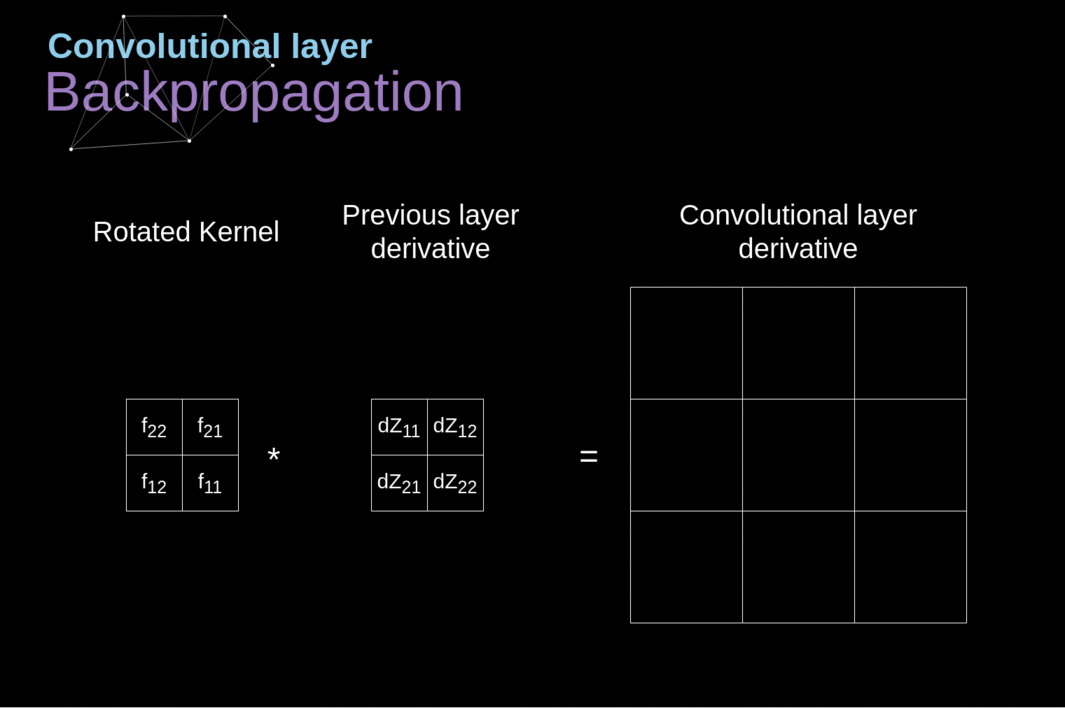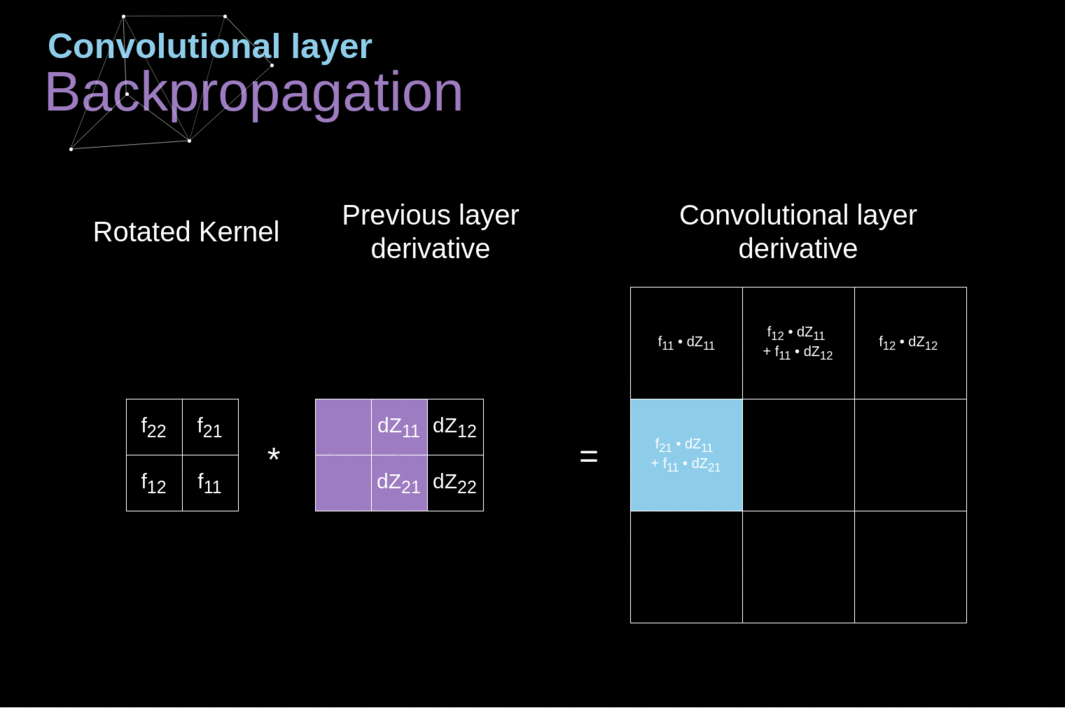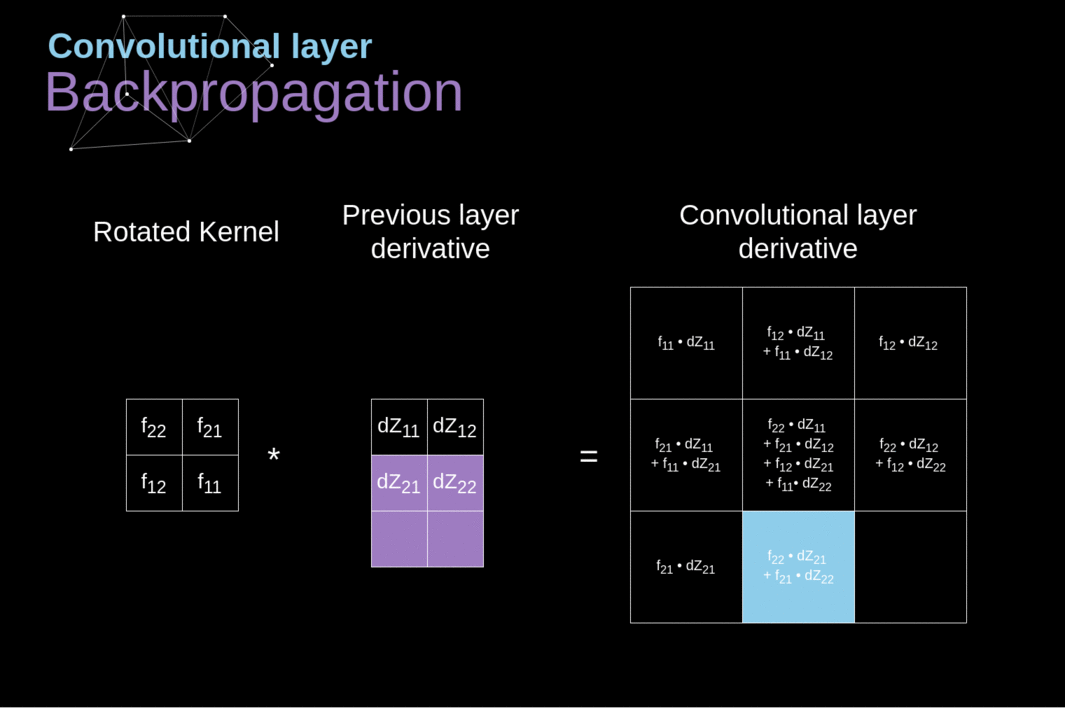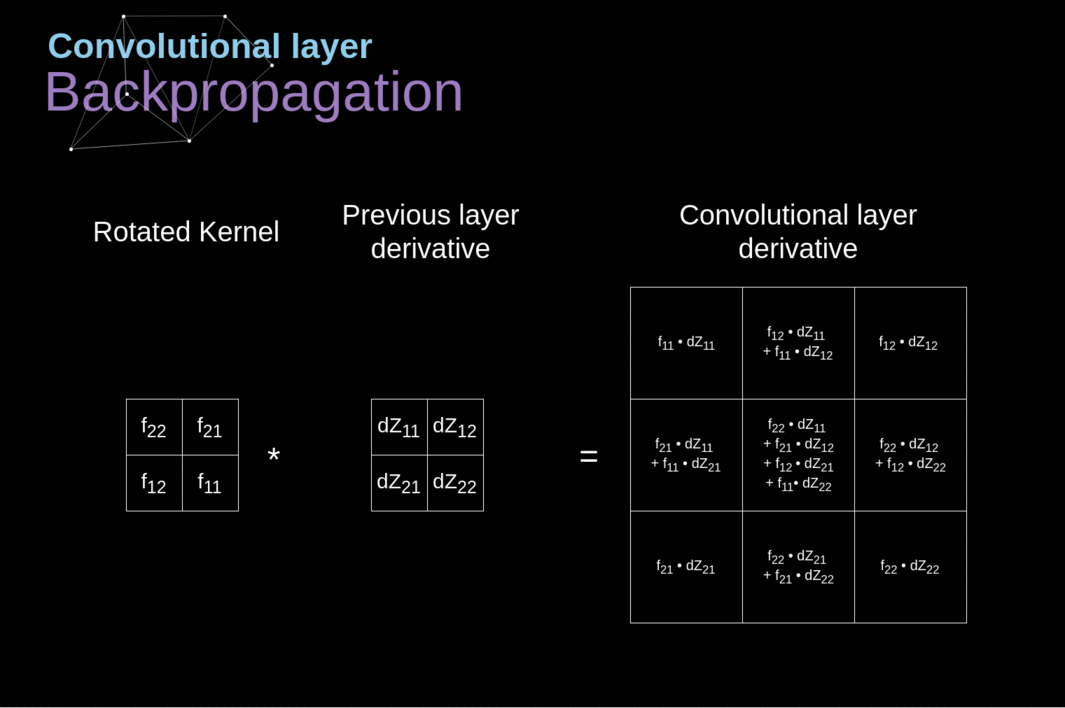 ######Figura 11. Convolução Completa
######Figura 11. Convolução Completa
Camadas de Agrupamento
Além das camadas de convolução, as CNNs frequentemente usam as chamadas camadas de pooling. Elas são usadas principalmente para reduzir o tamanho do tensor e acelerar os cálculos. Essas camadas são simples - precisamos dividir nossa imagem em diferentes regiões e, em seguida, realizar alguma operação para cada uma dessas partes. Por exemplo, para a Camada de Pooling Máximo, selecionamos o valor máximo de cada região e o colocamos no local correspondente na saída. Assim como no caso da camada de convolução, temos dois hiperparâmetros disponíveis - tamanho do filtro e passo (stride). Por último, mas não menos importante, se você estiver realizando pooling para uma imagem de vários canais, o pooling para cada canal deve ser feito separadamente.
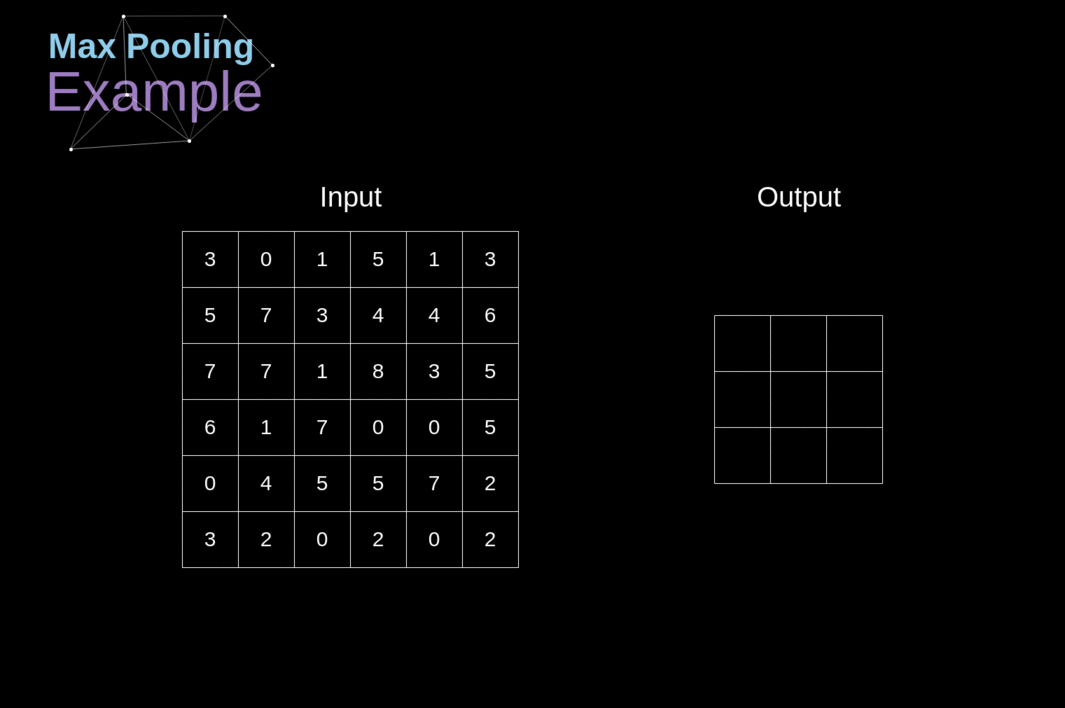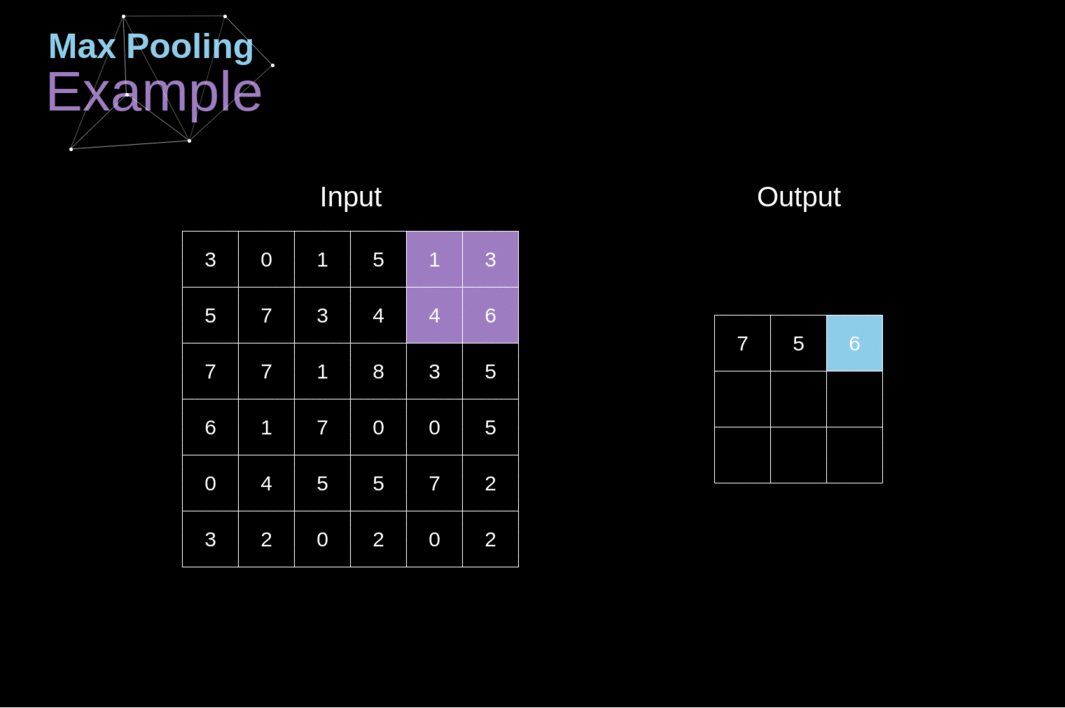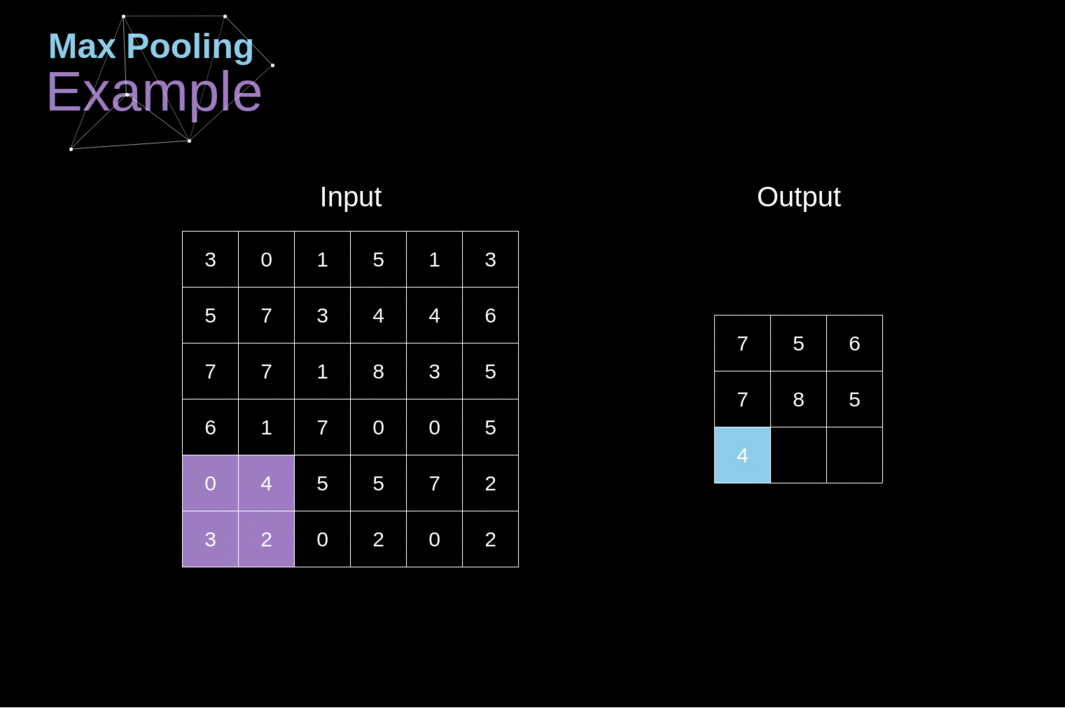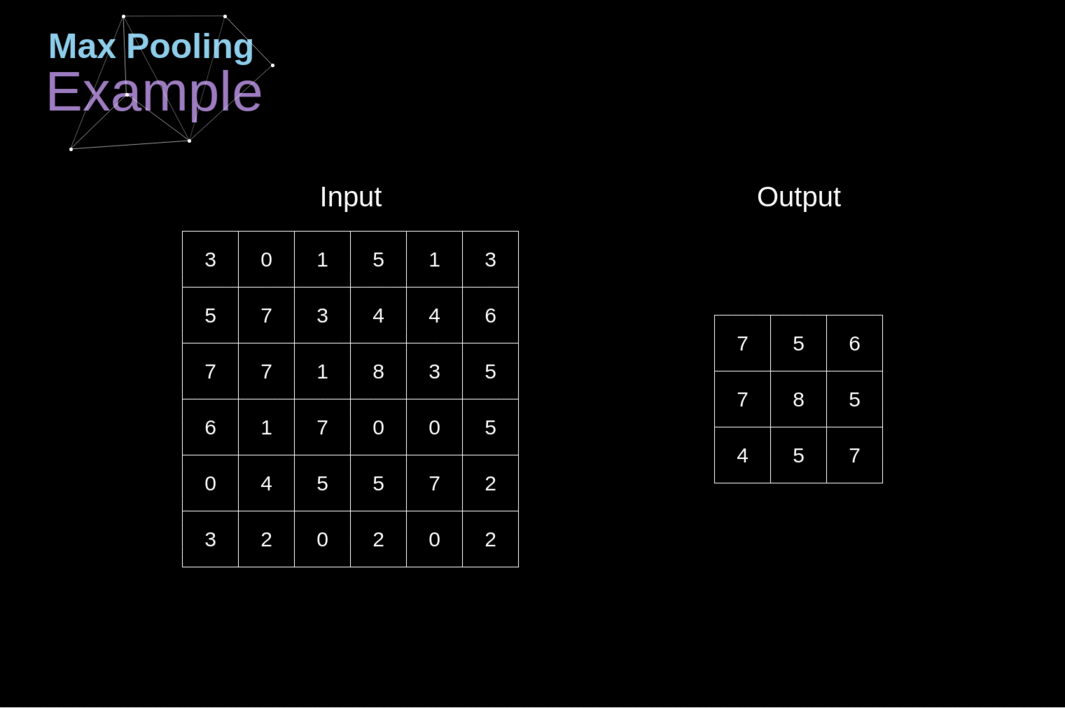 ######Figura 12. Exemplo de Pooling Máximo
######Figura 12. Exemplo de Pooling Máximo
Retropropagação nas Camadas de Pooling
Neste artigo, discutiremos apenas a retropropagação do pooling máximo, mas as regras que aprenderemos - com ajustes mínimos - são aplicáveis a todos os tipos de camadas de pooling. Como nesse tipo de camadas não temos nenhum parâmetro que precisaríamos atualizar, nossa tarefa é apenas distribuir gradientes adequadamente. Como lembramos, na propagação para frente do pooling máximo, selecionamos o valor máximo de cada região e os transferimos para a próxima camada. Portanto, é claro que durante a retropropagação, o gradiente não deve afetar elementos da matriz que não foram incluídos na passagem para frente. Na prática, isso é alcançado criando uma máscara que lembra a posição dos valores usados na primeira fase, que podemos depois utilizar para transferir os gradientes.
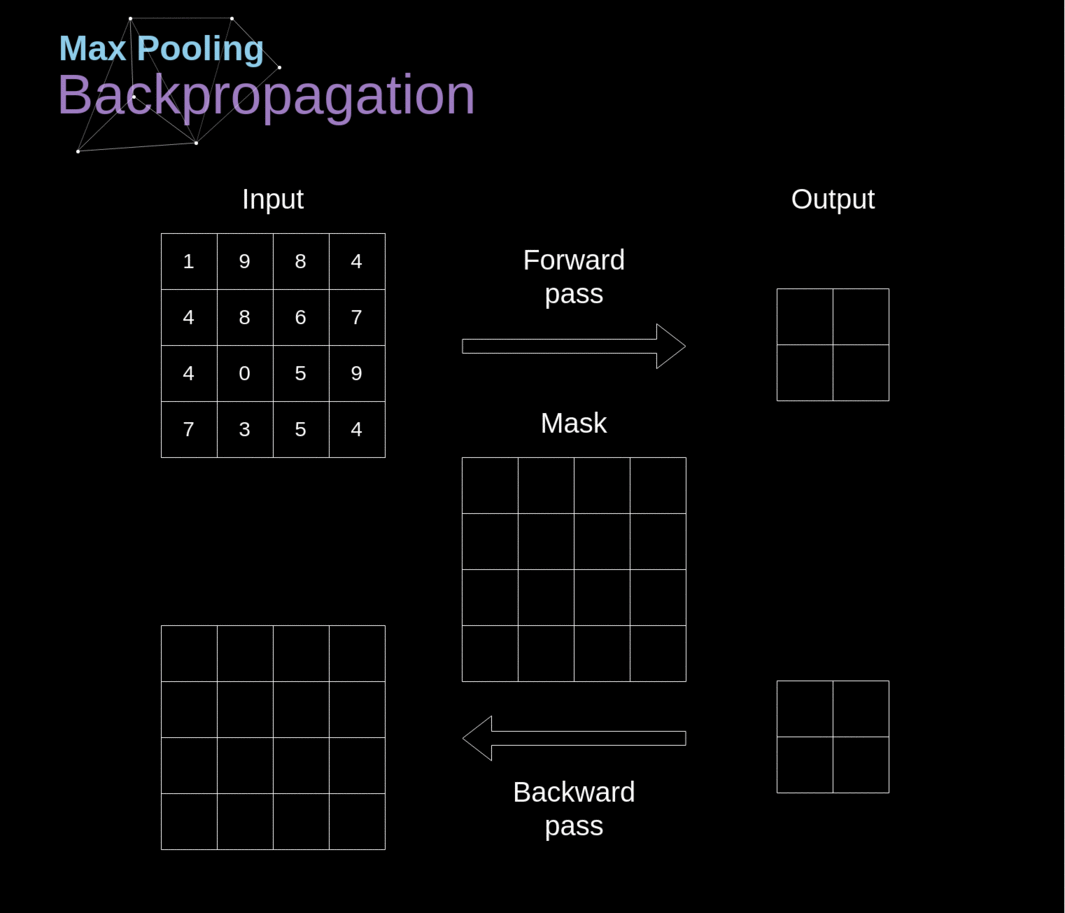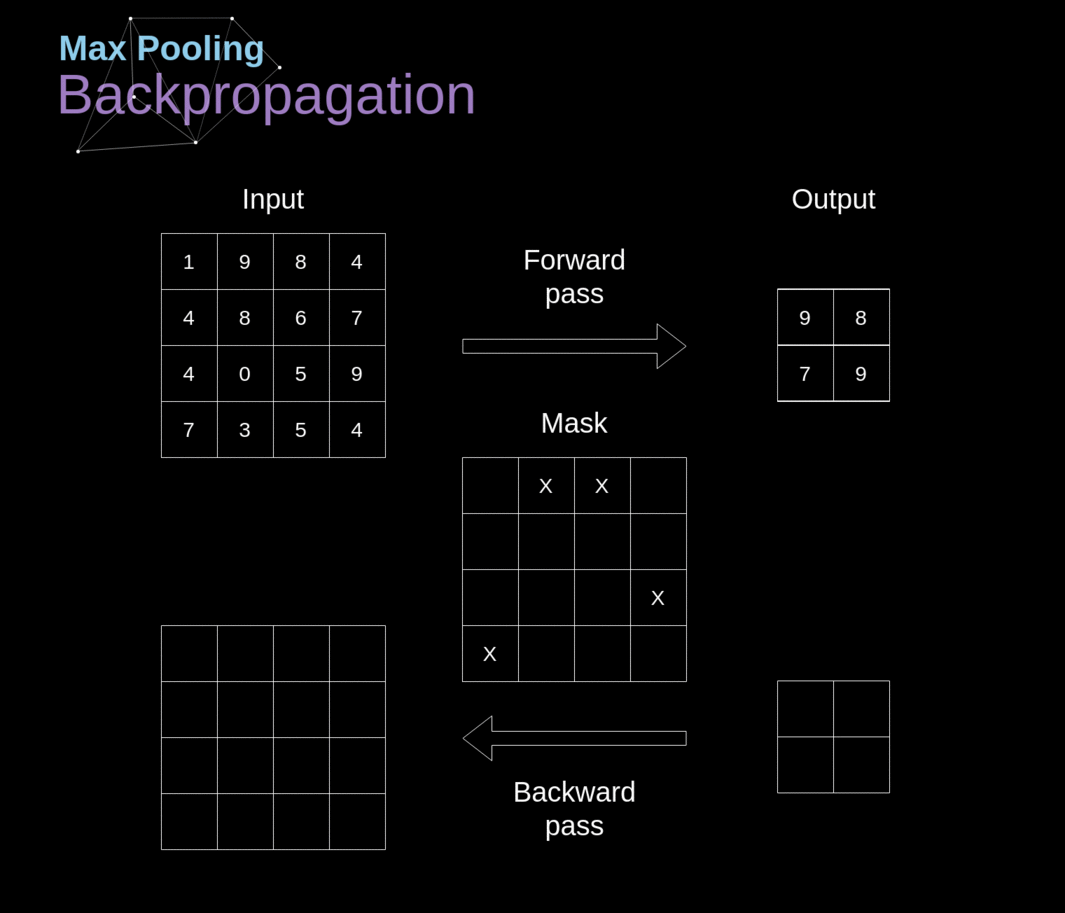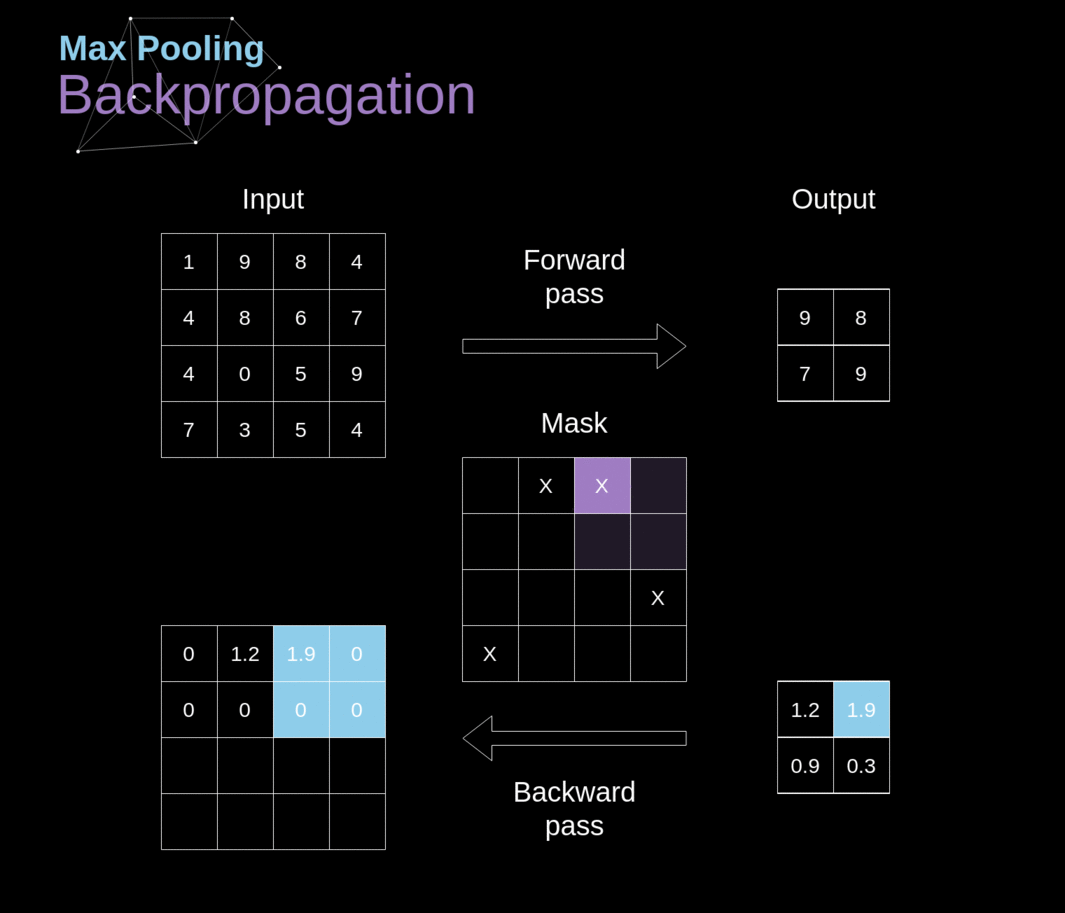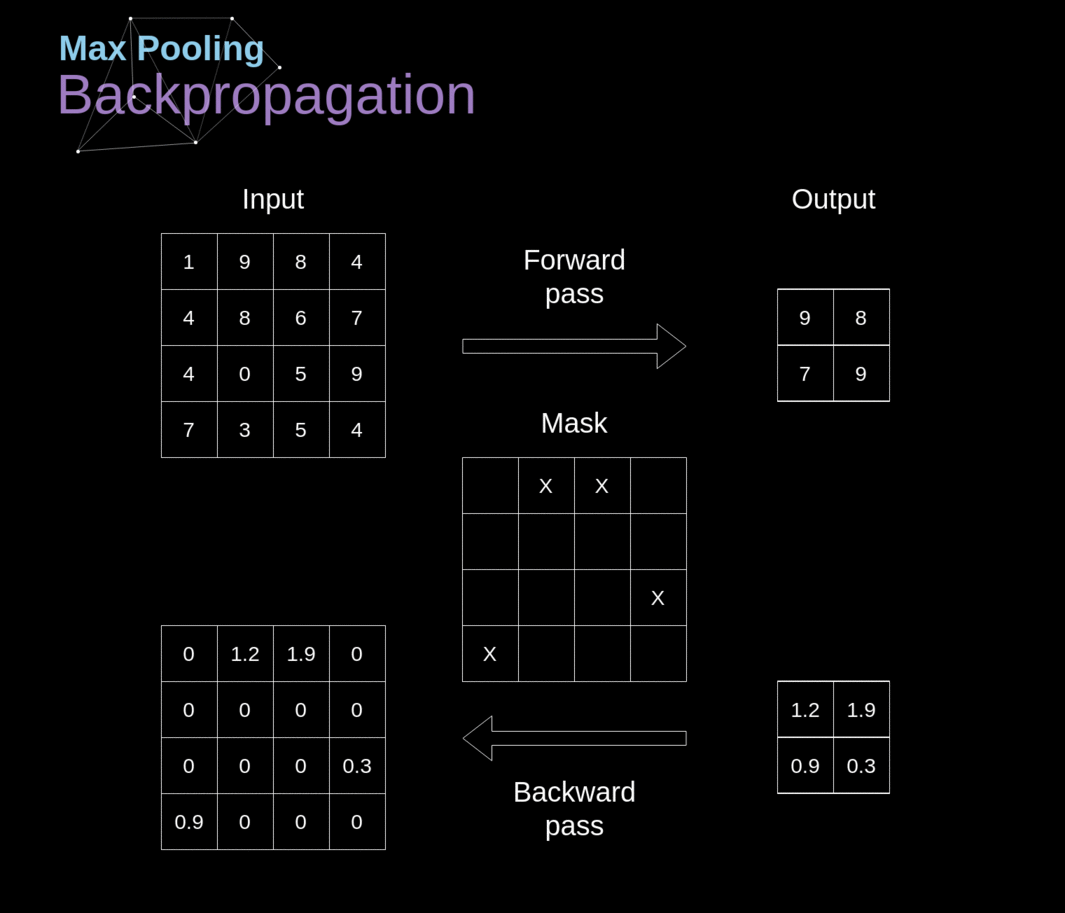 ######Figura 13. Retropropagação de Pooling Máximo
######Figura 13. Retropropagação de Pooling Máximo
Conclusão
Parabéns se você chegou até aqui. Muito obrigado pelo tempo dedicado à leitura deste artigo. Se você gostou do post, considere compartilhá-lo com seus amigos, um amigo, ou cinco amigos. Se você encontrou algum erro no pensamento, fórmulas, animações ou código, por favor, me avise.
Este artigo é mais uma parte da série "Mistérios das Redes Neurais", se você ainda não teve a oportunidade, leia os outros artigos. Além disso, se você gostou do meu trabalho até agora, siga-me no Twitter e Medium e veja outros projetos nos quais estou trabalhando, no GitHub e Kaggle. Mantenha-se curioso!
Artigo escrito por Piotr Skalski. Traduzido por Marcelo Panegali.

