Ir para o conteúdo
Buscar

WEB3DEV

Cover image for Um Guia Hacker para a Camada 2: Árvores de Merkle do Zero
Panegali
Panegali

Posted on

Um Guia Hacker para a Camada 2: Árvores de Merkle do Zero

#blockchain #zksnark #merkle

Neste tutorial, implementaremos árvores de Merkle (Merkle Trees), provas de Merkle e provas de Merkle delta em JavaScript a partir dos primeiros princípios.

Esta é a primeira parte semanal do Um Guia Hacker para a Camada 2: Construindo um zkVM a partir do zero.
Siga @cmpeq no twitter para ficar por dentro das próximas edições.

O que não posso criar, não entendo.

Richard Feynman

Introdução

As árvores de Merkle são uma das ferramentas mais importantes em qualquer caixa de ferramentas do desenvolvedor da camada 2. No espírito da abordagem de Feynman para entender um tópico, implementaremos árvores de Merkle do zero e construiremos uma profunda compreensão da árvore de Merkle que será essencial posteriormente em nossa jornada de desenvolvimento da camada 2.

Inventando árvores de Merkle: integridade de dados

Vamos imaginar que Jack queira enviar um arquivo de 400 gigabytes para sua amiga Sally por meio de uma conexão de internet não confiável. Levará horas para que o arquivo seja enviado, e Sally quer ter certeza de que o arquivo que ela recebe não seja corrompido ou alterado enquanto esteja sendo transferido.

Uma maneira de tentar resolver isso é fazer com que Jack crie uma assinatura digital de todo o arquivo e, em seguida, Sally verifique a assinatura quando a transferência do arquivo for concluída. Infelizmente, porém, a tecnologia de assinatura digital tem uma propriedade que: quanto mais longos forem os dados que você deseja assinar, mais lenta será a geração de uma assinatura digital, portanto, é impraticável para Jack assinar digitalmente todo o arquivo.

Eles podem contornar esse problema aproveitando a tecnologia de impressão digital (também conhecida como hashing criptográfico). Tirar o hash (ou impressão digital) de um arquivo grande gera um número curto de 32 bytes para representar os dados que sofreram hash. O mais importante é que, se você alterar até mesmo um único byte do arquivo grande, sua impressão digital também será alterada:

  1. Jack envia o hash, a assinatura e o arquivo para Sally.
  2. Quando Sally recebe o arquivo, ela calcula o hash em sua máquina e verifica se o hash corresponde ao que Jack assinou digitalmente.

Isso é muito bom, mas como a transferência pode levar horas e é muito provável que algo seja corrompido durante a transferência, Sally continua descobrindo que o hash que ela calcula é diferente daquele assinado por Jack e Jack precisa enviar o arquivo de 400 GB novamente (muito lento).

Uma maneira de corrigir isso seria fazer com que Jack primeiro dividisse o arquivo em duas partes (A e B) e processasse cada parte. Dessa forma, o tamanho de todos os dados que precisam ser reenviados é de 200 GB em vez de 400 GB.

Se Jack for realmente inteligente, ele poderá fazer com que tenha que computar apenas uma assinatura digital, assinando o Hash(Hash(A)+Hash(B)) (chamado de Root (Raíz)). Dessa forma, Sally sabe que os hashes de A e B não foram modificados durante a transferência e pode ter certeza de que o arquivo que ela recebe é o mesmo que o arquivo original de Jack. Se algum dado em A ou B for modificado, Hash(Hash(A)+Hash(B)) não corresponderá à assinatura original de Jack.

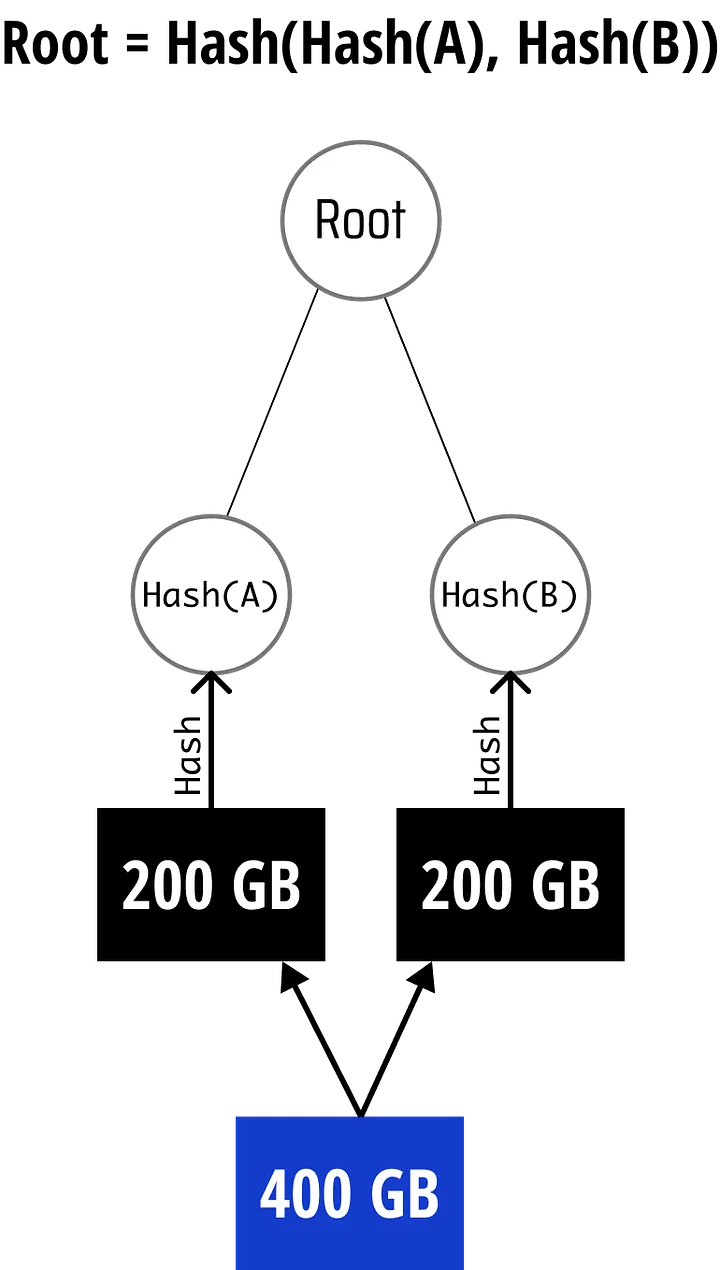Divida o arquivo em duas partes, faça o hash de cada parte e, em seguida, faça o hash da combinação dos hashes das duas partes

Na verdade, podemos dividir o arquivo em partes ainda menores para tornar o tamanho de qualquer dado que precise ser reenviado muito menor:

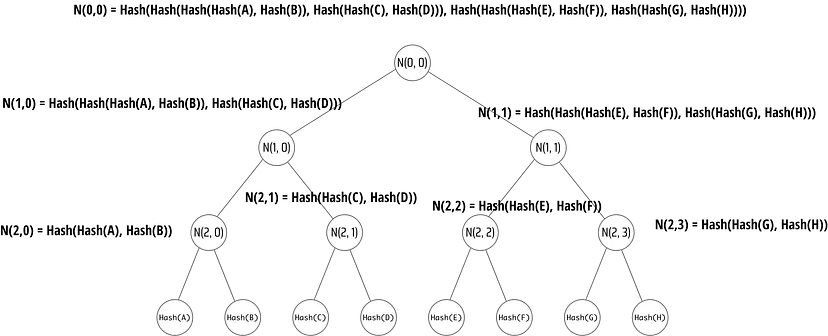Se Jack dividisse o arquivo em 8 partes, ele criaria uma estrutura como esta e assinaria N(0,0)

Esse negócio de dividir dados e hashing recursivamente é chamado de construção de uma árvore de Merkle.

Como em nosso exemplo, o princípio básico de uma árvore de Merkle é:
se você modificar o valor de qualquer um dos nós na parte inferior, que representam nosso conjunto de dados, o valor do nó no topo também mudará.

Os nós na parte inferior que contêm nosso conjunto de dados são conhecidos como folhas e o nó na parte superior (também conhecido como N(0,0)) é conhecido como Raízes de Merkle (Merkle Root).

Por conveniência, podemos identificar cada nó N com dois números:

  1. O nível (level) do nó (o nó superior está no nível 0 e os nós abaixo dele têm nível = 1 etc.).
  2. O índice (index) do nó (para o índice, contamos apenas da esquerda para a direita com o nó mais à esquerda tendo índice = 0).

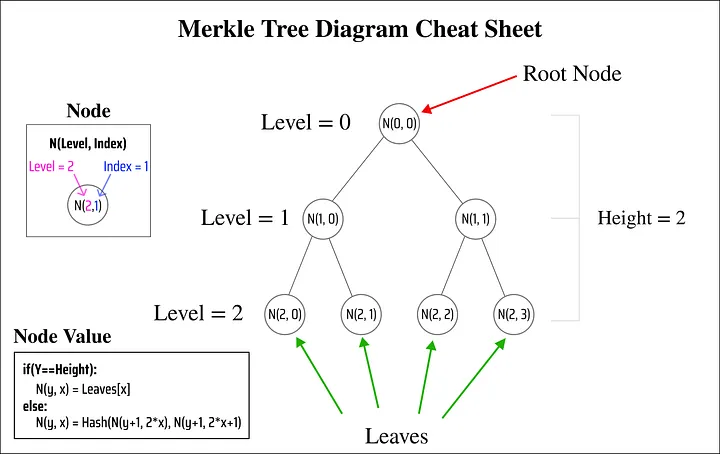Folha de consulta da árvore de Merkle

Usando nossa definição de nó, também podemos dizer que todo nó N(nível, índice) tem dois filhos N(nível+1, índice*2) e N(nível+1, índice*2+1). Isso é para refletir que cada nível tem o dobro de nós do nível acima dele.

Além disso, usando nossa regra anterior de computação Hash(Hash(A), Hash(B)), podemos definir o valor de cada nó não folha como: N(nível, índice) = Hash(N(nível+1, índice*2), N(nível+1, índice*2+1)).

Também podemos definir a altura da árvore de Merkle como a distância entre as folhas e a raiz de Merkle (ou seja, contar as linhas no caminho entre os nós da folha e o nó da raiz no topo). As folhas da árvore de Merkle sempre têm um número de nível igual à altura da árvore.

Codificando uma árvore de Merkle

Agora que inventamos a árvore de Merkle, podemos demonstrar nosso novo conhecimento escrevendo uma implementação em JavaScript.

Primeiro, precisamos selecionar uma função para calcular nossas impressões digitais. Podemos usar a função de hashing sha256 comum para computar Hash(childA, childB):

const shajs = require("sha.js"); // instala o npm --salva sha.js

function hash(leftNode, rightNode) {
  return shajs("sha256")
    .update(leftNode + rightNode, "hex")
    .digest("hex");
}
Enter fullscreen mode Exit fullscreen mode

Com uma função hash em mãos, podemos escrever uma classe simples que calcula a raiz de Merkle com um conjunto de dados de folhas e a altura da árvore correspondente:

const shajs = require("sha.js"); // instala o npm --salva sha.js

function hash(leftNode, rightNode) {
  return shajs("sha256")
    .update(leftNode + rightNode, "hex")
    .digest("hex");
}

class MerkleTree {
  constructor(height, leaves){
    this.height = height;
    this.leaves = leaves;
  }
  N(level, index){
    if(level === this.height){
      // se level == height, o nó é uma folha, 
      // portanto, basta retornar o valor de nosso conjunto de dados
      return this.leaves[index];
    }else{
      // se o nó não for uma folha, use nossa definição:
      // N(level, index) = Hash(N(level+1, index*2), N(level+1, index*2+1))
      return hash(
        this.N(level+1, 2*index),
        this.N(level+1, 2*index+1),
      );
    }
  }
  getRoot(){
    // o nó N(0,0) é sempre o nó raiz
    return this.N(0,0);
  }
}
Enter fullscreen mode Exit fullscreen mode

Vamos testar nossa implementação da árvore de Merkle com uma árvore que tem folhas = [1, 3, 3, 7, 4, 2, 0, 6] e uma altura de 3:

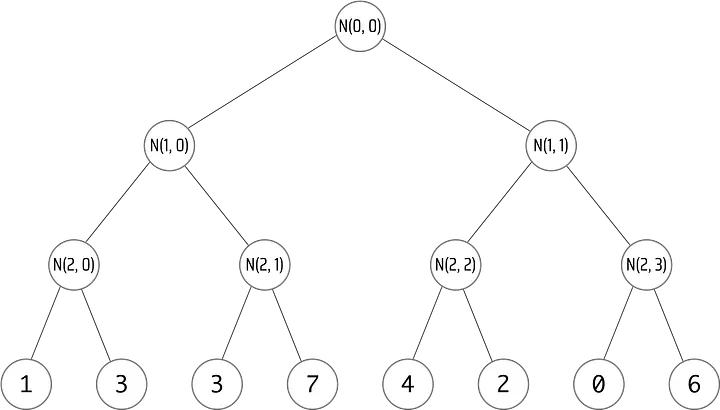Uma árvore com folhas = [1, 3, 3, 7, 4, 2, 0, 6] e uma altura de 3

Em nosso arquivo JavaScript, podemos escrever cada folha como uma string hexadecimal, criar uma nova instância da árvore de Merkle e chamar a função getRoot para calcular a raiz:

function example1(){
  const height = 3;
  const leaves = [
    "0000000000000000000000000000000000000000000000000000000000000001", // 1
    "0000000000000000000000000000000000000000000000000000000000000003", // 3
    "0000000000000000000000000000000000000000000000000000000000000003", // 3
    "0000000000000000000000000000000000000000000000000000000000000007", // 7
    "0000000000000000000000000000000000000000000000000000000000000004", // 4
    "0000000000000000000000000000000000000000000000000000000000000002", // 2
    "0000000000000000000000000000000000000000000000000000000000000000", // 0
    "0000000000000000000000000000000000000000000000000000000000000006", // 6
  ];
  const tree = new MerkleTree(height, leaves);
  console.log("[EX_1] the merkle tree's root is: "+tree.getRoot());
}
example1();
Enter fullscreen mode Exit fullscreen mode

Se executarmos este código, obteremos a saída:

[EX_1] the merkle tree's root is: 7e286a6721a66675ea033a4dcdec5abbdc7d3c81580e2d6ded7433ed113b7737
Enter fullscreen mode Exit fullscreen mode

Se mudarmos alguma das folhas (por exemplo, trocando o 2 por um 9), veremos também que a raiz muda:

function example2(){
  const height = 3;
  const leaves = [
    "0000000000000000000000000000000000000000000000000000000000000001", // 1
    "0000000000000000000000000000000000000000000000000000000000000003", // 3
    "0000000000000000000000000000000000000000000000000000000000000003", // 3
    "0000000000000000000000000000000000000000000000000000000000000007", // 7
    "0000000000000000000000000000000000000000000000000000000000000004", // 4
    "0000000000000000000000000000000000000000000000000000000000000002", // 2
    "0000000000000000000000000000000000000000000000000000000000000000", // 0
    "0000000000000000000000000000000000000000000000000000000000000006", // 6
  ];
  const tree = new MerkleTree(height, leaves);
  console.log("[EX_2] before root is: "+tree.getRoot());
  // mudar o 2 por um 9
  tree.leaves[5] = "0000000000000000000000000000000000000000000000000000000000000009";
  console.log("[EX_2] after root is: "+tree.getRoot());
}
example2();
Enter fullscreen mode Exit fullscreen mode

Se executarmos example2(), veremos a saída:

[EX_2] before root is: 7e286a6721a66675ea033a4dcdec5abbdc7d3c81580e2d6ded7433ed113b7737
[EX_2] after root is: e74ae221cf067dc8e88195f5b30bfda60dc224a8cd5554bc6345c87ad8c6f925
Enter fullscreen mode Exit fullscreen mode

Sucesso! A raiz antes da alteração corresponde à nossa raiz original porque tinha o mesmo conjunto de dados e a raiz posterior foi atualizada porque alteramos uma das folhas no conjunto de dados.

Vamos analisar mais profundamente por que mudar uma das folhas muda a raiz:

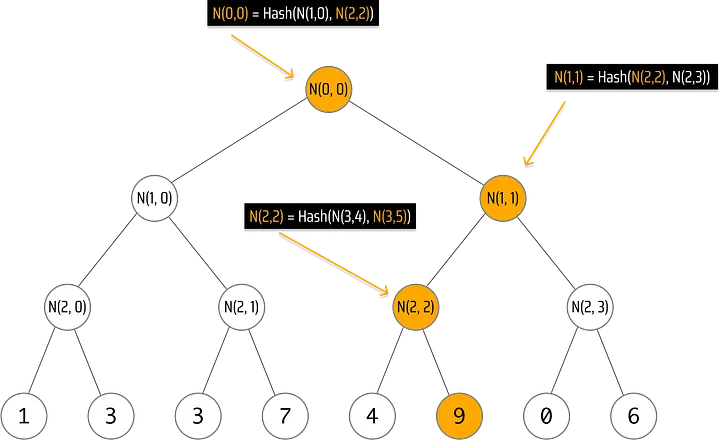Os efeitos da mudança da folha N(3,5) de 2 para 9 sobem na árvore
  • Como alteramos N(3,5), seu pai N(2,2) muda porque N(2,2) é definido como N(2,2) = Hash(N(3,4), N(3,5)).
  • Como N(2,2) mudou, seu pai N(1,1) muda porque N(1,1) é definido como N(1,1) = Hash( N(2,2), N(2,3)).
  • Como N(1,1) mudou, seu pai N(0,0) muda porque N(0,0) é definido como N(0,0) = Hash(N(1,0), N(1,1)).

Os nós que mudam quando você atualiza uma folha são chamados de caminho de Merkle do nó. Portanto, neste caso, poderíamos dizer que o caminho de Merkle de N(3,5) é [N(3,5), N(2,2), N(1,1), N(0,0)].

Para calcular o caminho de Merkle de um nó, apenas listamos recursivamente os antepassados do nó. (antepassados ​​= pai do nó, pai do pai, pai do pai do pai…).

Como sabemos anteriormente que cada nó N(level, index), tem dois filhos N(level+1, index*2) e N(level+1, index*2+1), podemos dizer que o pai de um nó N(level, index) é N(level-1, floor(index/2)).

Usando esse conhecimento, podemos escrever uma função JavaScript para calcular o caminho de Merkle de um nó e verificar nossa observação anterior com N(3,5):

function getMerklePathOfNode(level, index){
  const merklePath = [];
  for(let currentLevel=level;currentLevel>=0;currentLevel--){
    merklePath.push({
      level: currentLevel,
      index: index,
    });
    index = Math.floor(index/2);
  }
  return merklePath;
}

console.log(getMerklePathOfNode(3,5))
Enter fullscreen mode Exit fullscreen mode

Quando o executamos, o log imprime [N(3,5), N(2,2), N(1,1), N(0,0)]:

[
  { level: 3, index: 5 },
  { level: 2, index: 2 },
  { level: 1, index: 1 },
  { level: 0, index: 0 }
]
Enter fullscreen mode Exit fullscreen mode

Na prática, geralmente excluímos o nó raiz do nosso caminho de Merkle retornado, pois o caminho de Merkle de cada nó o contém, para que possamos reescrever nossa função para retornar todos os nós no caminho de Merkle, exceto a raiz (nível>0):

function getMerklePathOfNode(level, index){
  const merklePath = [];
  for(let currentLevel=level;currentLevel>0;currentLevel--){
    merklePath.push({
      level: currentLevel,
      index: index,
    });
    index = Math.floor(index/2);
  }
  return merklePath;
}
Enter fullscreen mode Exit fullscreen mode

Irmãos

Antes de continuarmos, é importante falarmos sobre o conceito de nós canhotos e destros em uma árvore de Merkle.

  • Dizemos que um nó é canhoto se ele aparece na árvore do lado esquerdo de seu pai.
  • Dizemos que um nó é destro se ele aparece na árvore do lado direito de seu pai.

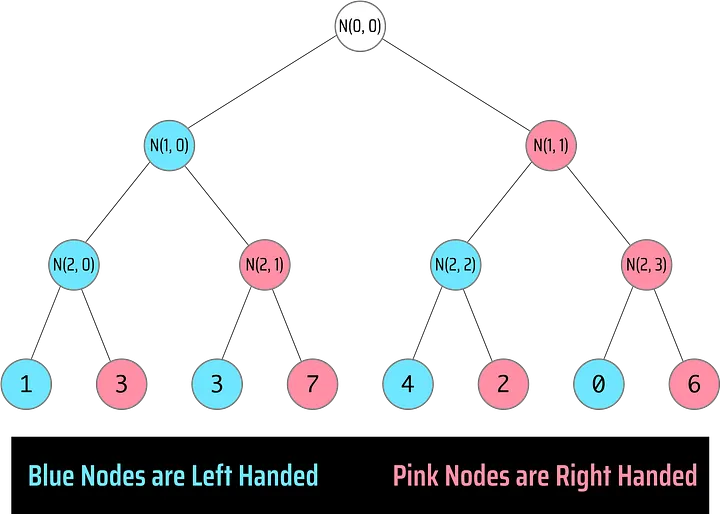
Dada nossa definição original da árvore de Merkle, onde dizemos que todo nó não-folha N(level, index) tem um filho esquerdo e um filho direito:

  • Filho Esquerdo: N(level+1, 2*index)
  • Filho Direito: N(level+1, 2*index + 1)

Dada essa definição, podemos ver que todos os nós canhotos têm um índice par (2*x) e os nós destros têm um índice ímpar (2*x+1).

Portanto:

  • Se um nó N(level, index) tiver um índice par, dizemos que seu irmão oposto é N(level, index+1).
  • Se um nó N(level, index) tem um índice ímpar, dizemos que seu irmão oposto é N(level, index-1).

Vamos escrever uma função JavaScript para retornar o irmão de qualquer nó que especificamos em uma árvore:

function getSiblingNode(level, index){
  // se o nó for a raiz, ele não terá irmãos
  if(level === 0){
    throw new Error("a raiz nao tem um irmao")
  }else if(index % 2 === 0){
    // se o nó for par, seu irmão está no índice+1
    return {level: level, index: index+1};
  }else{
    // se o nó for ímpar, seu irmão está no índice-1
    return {level: level, index: index-1};
  }
}
Enter fullscreen mode Exit fullscreen mode

Provas de Merkle

Frequentemente, queremos provar a inclusão de uma determinada folha em uma árvore de Merkle com uma raiz conhecida. Vamos imaginar que Bob queira provar a seu amigo Todd que o valor 9 existe na folha N(3,5) em uma árvore com uma raiz de Merkle conhecida R.

A maneira mais ingênua de Bob fazer isso é:

  1. Bob dá a Todd uma lista de todas as folhas.
  2. Todd usa nossa classe MerkleTree para calcular N(0,0).
  3. Todd compara N(0,0) com R para ter certeza de que são iguais.

Para árvores grandes, no entanto, isso não é muito prático. Se Bob quiser provar o valor de uma folha em uma árvore com 1.000.000 de folhas, Bob deve enviar todas as 1.000.000 de folhas para Todd e, Todd deve fazer 999.999 cálculos para calcular a raiz.

Se olharmos novamente para o nosso diagrama de caminho de Merkle, no entanto, há uma maneira mais rápida de fazer isso:

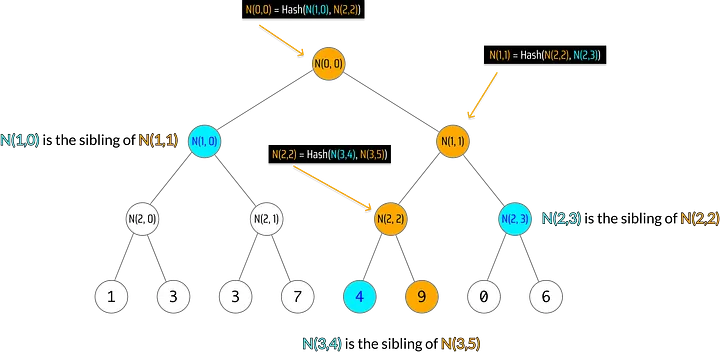Os irmãos do caminho de Merkle de N(3,5) estão destacados em azul

Em nosso diagrama, podemos ver que Todd pode calcular a raiz se Bob fornecer a ele: o valor da folha, o índice da folha e os irmãos dos nós não raiz no caminho de Merkle da folha (N(3,4), N(2,3) e N(1,0)):

N(0,0) = Hash(N(1,0), Hash(Hash(N(3,4), 9), N(2,3)))

Usando esse método, para uma árvore com N folhas, Todd só precisa calcular log(N), portanto, se a árvore tiver 1.000.000 de folhas, ele só precisará realizar 20 cálculos em vez de 999.999 cálculos!

O valor, o índice e os irmãos juntos são conhecidos como prova de Merkle, pois são os principais elementos necessários para provar a existência de uma folha em uma árvore de Merkle com uma raiz conhecida.

Vamos primeiro escrever uma função para calcular os irmãos do caminho de Merkle de um determinado nó:

Vamos atualizar nossa classe MerkleTree para incluir uma função getMerkleProof:

class MerkleTree {
// ...
getMerkleProof(level, index){

    // obtém o valor do nó folha
    const leafValue = this.N(level, index);

    // obtém os níveis e índices dos nós no caminho de Merkle da folha
    const merklePath = getMerklePathOfNode(level, index);

    // obtém os níveis e índices dos irmãos dos nós no caminho de Merkle
    const merklePathSiblings = merklePath.map((node) => {
      return getSiblingNode(node.level, node.index);
    });

    // obtém os valores dos nós irmãos
    const siblingValues = merklePathSiblings.map((node) => {
      return this.N(node.level, node.index);
    });

    return {
      root: this.getRoot(), // a raiz que afirmamos ser a raiz de nossa árvore
      siblings: siblingValues, // os irmãos do caminho de Merkle de nossa folha
      index: index, // o índice de nossa folha
      value: leafValue, // o valor de nossa folha
    };
  }
}
Enter fullscreen mode Exit fullscreen mode

Também podemos escrever uma função que calcula a raiz de Merkle usando os irmãos, índice e valor da prova:

function computeMerkleRootFromProof(siblings, index, value){
  // inicia nosso caminho de nó de Merkle no nó folha
  let merklePathNodeValue = value;
  let merklePathNodeIndex = index;

  // seguimos o caminho de Merkle da folha até a raiz, calculando os nós do caminho de Merkle usando os irmãos fornecidos à medida que avançamos sozinhos
  for(let i=0;i<siblings.length;i++){
    const merklePathNodeSibling = siblings[i];

    if(merklePathNodeIndex%2===0){
      // se o índice atual do nó em nosso caminho de Merkle for par:
      // * merklePathNodeValue é o nó esquerdo,
      // * merklePathNodeSibling é o nó direito
      // * o valor do nó pai é um hash(merklePathNodeValue, merklePathNodeSibling)
      merklePathNodeValue = hash(merklePathNodeValue, merklePathNodeSibling);
    }else{
      // se o índice atual do nó em nosso caminho de Merkle for ímpar:
      // * merklePathNodeSibling é o nó esquerdo
      // * merklePathNodeValue é o nó direito,
      // * o valor do nó pai é hash(merklePathNodeSibling, merklePathNodeValue)
      merklePathNodeValue = hash(merklePathNodeSibling, merklePathNodeValue);
    }

    // usando nossa definição, o nó pai de nosso nó de caminho é N(level-1, floor(index/2))
    merklePathNodeIndex = Math.floor(merklePathNodeIndex/2);
  }
  return merklePathNodeValue;
}
Enter fullscreen mode Exit fullscreen mode

Finalmente, vamos escrever uma função que verifica a prova de Merkle:

function verifyMerkleProof(proof){
  return proof.root === computeMerkleRootFromProof(proof.siblings, proof.index, proof.value);
}
Enter fullscreen mode Exit fullscreen mode

Juntando tudo, agora temos uma classe que pode gerar uma prova de Merkle de inclusão que pode ser verificada em tempo O(log(n)).

const shajs = require("sha.js"); // instala o npm --salva sha.js

function hash(leftNode, rightNode) {
  return shajs("sha256")
    .update(leftNode + rightNode, "hex")
    .digest("hex");
}
function getSiblingNode(level, index){
  // se o nó for a raiz, ele não terá irmãos
  if(level === 0){
    throw new Error("a raiz nao tem um irmao")
  }else if(index % 2 === 0){
    // se o nó for par, seu irmão está no índice+1
    return {level: level, index: index+1};
  }else{
    // se o nó for ímpar, seu irmão está no índice-1
    return {level: level, index: index-1};
  }
}
function getMerklePathOfNode(level, index){
  const merklePath = [];
  for(let currentLevel=level;currentLevel>0;currentLevel--){
    merklePath.push({
      level: currentLevel,
      index: index,
    });
    index = Math.floor(index/2);
  }
  return merklePath;
}
class MerkleTree {
  constructor(height, leaves){
    this.height = height;
    this.leaves = leaves;
  }
  N(level, index){
    if(level === this.height){
      // se level == height, o nó é uma folha, portanto, basta retornar o valor do nosso conjunto de dados
      return this.leaves[index];
    }else{
      // se o nó não for uma folha, use nossa definição:
      // N(level, index) = Hash(N(level+1, index*2), N(level+1, index*2+1))
      return hash(
        this.N(level+1, 2*index),
        this.N(level+1, 2*index+1),
      );
    }
  }
  getRoot(){
    // o nó N(0,0) é sempre o nó raiz
    return this.N(0,0);
  }
  getMerkleProof(level, index){

    // obtém o valor do nó folha
    const leafValue = this.N(level, index);

    // obtém os níveis e índices dos nós no caminho de Merkle da folha
    const merklePath = getMerklePathOfNode(level, index);

    // obtém os níveis e índices dos irmãos dos nós no caminho de Merkle
    const merklePathSiblings = merklePath.map((node) => {
      return getSiblingNode(node.level, node.index);
    });

    // obtém os valores dos nós irmãos
    const siblingValues = merklePathSiblings.map((node) => {
      return this.N(node.level, node.index);
    });

    return {
      root: this.getRoot(), // a raiz que afirmamos ser a raiz de nossa árvore
      siblings: siblingValues, // os irmãos do caminho de Merkle de nossa folha
      index: index, // o índice de nossa folha
      value: leafValue, // o valor de nossa folha
    };
  }
}
function computeMerkleRootFromProof(siblings, index, value){
  // iniciar nosso caminho de nó Merkle no nó folha
  let merklePathNodeValue = value;
  let merklePathNodeIndex = index;

  // seguimos o caminho do Merkle da folha até a raiz, calculando os nós do caminho do Merkle usando os irmãos fornecidos à medida que avançamos sozinhos
  for(let i=0;i<siblings.length;i++){
    const merklePathNodeSibling = siblings[i];

    if(merklePathNodeIndex%2===0){
      // se o índice atual do nó em nosso caminho de Merkle for par:
      // * merklePathNodeValue é o nó esquerdo,
      // * merklePathNodeSibling é o nó direito
      // * o valor do nó pai é hash(merklePathNodeValue, merklePathNodeSibling)
      merklePathNodeValue = hash(merklePathNodeValue, merklePathNodeSibling);
    }else{
      // se o índice atual do nó em nosso caminho de Merkle for ímpar:
      // * merklePathNodeSibling é o nó esquerdo,
      // * merklePathNodeValue é o nó direito,
      // * o valor do nó pai é hash(merklePathNodeSibling, merklePathNodeValue)
      merklePathNodeValue = hash(merklePathNodeSibling, merklePathNodeValue);
    }

    // Usando nossa definição, o nó pai de nosso nó de caminho é  N(level-1, floor(index/2))
    merklePathNodeIndex = Math.floor(merklePathNodeIndex/2);
  }
  return merklePathNodeValue;
}
function verifyMerkleProof(proof){
  return proof.root === computeMerkleRootFromProof(proof.siblings, proof.index, proof.value);
}
function example4(){
  const height = 3;
  const leaves = [
    "0000000000000000000000000000000000000000000000000000000000000001", // 1
    "0000000000000000000000000000000000000000000000000000000000000003", // 3
    "0000000000000000000000000000000000000000000000000000000000000003", // 3
    "0000000000000000000000000000000000000000000000000000000000000007", // 7
    "0000000000000000000000000000000000000000000000000000000000000004", // 4
    "0000000000000000000000000000000000000000000000000000000000000009", // 9
    "0000000000000000000000000000000000000000000000000000000000000000", // 0
    "0000000000000000000000000000000000000000000000000000000000000006", // 6
  ];
  const tree = new MerkleTree(height, leaves);
  console.log("[EX_4] the root is: "+tree.getRoot());
  const merkleProofOfN3_5 = tree.getMerkleProof(3,5);

  console.log("[EX_4] the merkle proof of N(3,5):\n" + JSON.stringify(merkleProofOfN3_5, null, 2));

  console.log("[EX_4] computed root: "+computeMerkleRootFromProof(merkleProofOfN3_5.siblings, merkleProofOfN3_5.index, merkleProofOfN3_5.value));
  console.log("[EX_4] verify merkle proof: "+verifyMerkleProof(merkleProofOfN3_5));
}

example4();
Enter fullscreen mode Exit fullscreen mode

Isso imprime:

[EX_4] the root is: e74ae221cf067dc8e88195f5b30bfda60dc224a8cd5554bc6345c87ad8c6f925
[EX_4] the merkle proof of N(3,5):
{
  "root": "e74ae221cf067dc8e88195f5b30bfda60dc224a8cd5554bc6345c87ad8c6f925",
  "siblings": [
    "0000000000000000000000000000000000000000000000000000000000000004",
    "deb2a27a00dbc46e3a59096a8d07d2b97f950158886411ff6a9c9ab9623dada6",
    "2f4d3e941b602c50347af3f5c809a28737c27c7ce460e77b10739875ef957aa7"
  ],
  "index": 5,
  "value": "0000000000000000000000000000000000000000000000000000000000000009"
}
[EX_4] computed root: e74ae221cf067dc8e88195f5b30bfda60dc224a8cd5554bc6345c87ad8c6f925
[EX_4] verify merkle proof: true
Enter fullscreen mode Exit fullscreen mode

Provas de Merkle Delta

Se tivermos uma árvore de Merkle com raiz A e gerarmos uma prova de Merkle que tenha irmãos, além de provar que uma determinada folha existe em uma árvore de Merkle, muitas vezes queremos provar o resultado da modificação de uma folha específica em uma árvore de um valor para outro. Isso é chamado de prova de Merkle delta (delta significa mudança).

Em particular, as provas de Merkle delta provam que:

  • Uma folha existe no índice I com valor X em uma árvore com raiz de Merkle A.
  • Se você alterar o valor da folha com índice I de X para Y sem modificar nenhuma outra folha na árvore, a nova raiz de Merkle da árvore será B.

Já sabemos como provar “Existe uma folha no índice I com valor X em uma árvore com raiz de Merkle A”; podemos apenas chamar a função getMerkleProof em nosso contrato.

Se então modificarmos a folha, digamos de 9 para 8, vamos chamar getMerkleProof novamente e ver o que acontece:

function example5(){
  const height = 3;
  const leaves = [
    "0000000000000000000000000000000000000000000000000000000000000001", // 1
    "0000000000000000000000000000000000000000000000000000000000000003", // 3
    "0000000000000000000000000000000000000000000000000000000000000003", // 3
    "0000000000000000000000000000000000000000000000000000000000000007", // 7
    "0000000000000000000000000000000000000000000000000000000000000004", // 4
    "0000000000000000000000000000000000000000000000000000000000000009", // 9
    "0000000000000000000000000000000000000000000000000000000000000000", // 0
    "0000000000000000000000000000000000000000000000000000000000000006", // 6
  ];
  const tree = new MerkleTree(height, leaves);
  const beforeMerkleProofOfN3_5 = tree.getMerkleProof(3,5);
  console.log("[EX_5] the merkle proof of N(3,5) before change:\n" + JSON.stringify(beforeMerkleProofOfN3_5, null, 2));
  // mudar 9 para 8
  tree.leaves[5] = "0000000000000000000000000000000000000000000000000000000000000008";

  const afterMerkleProofOfN3_5 = tree.getMerkleProof(3,5);
  console.log("[EX_5] the merkle proof of N(3,5) after change:\n" + JSON.stringify(afterMerkleProofOfN3_5, null, 2));
}
example5();
Enter fullscreen mode Exit fullscreen mode

Isso imprime:

[EX_5] the merkle proof of N(3,5) before change:
{
  "root": "e74ae221cf067dc8e88195f5b30bfda60dc224a8cd5554bc6345c87ad8c6f925",
  "siblings": [
    "0000000000000000000000000000000000000000000000000000000000000004",
    "deb2a27a00dbc46e3a59096a8d07d2b97f950158886411ff6a9c9ab9623dada6",
    "2f4d3e941b602c50347af3f5c809a28737c27c7ce460e77b10739875ef957aa7"
  ],
  "index": 5,
  "value": "0000000000000000000000000000000000000000000000000000000000000009"
}
[EX_5] the merkle proof of N(3,5) after change:
{
  "root": "99ba6856d11cd514be35ed291e86ae7957ec43d6b83270f32aaa50a8a25dc5cc",
  "siblings": [
    "0000000000000000000000000000000000000000000000000000000000000004",
    "deb2a27a00dbc46e3a59096a8d07d2b97f950158886411ff6a9c9ab9623dada6",
    "2f4d3e941b602c50347af3f5c809a28737c27c7ce460e77b10739875ef957aa7"
  ],
  "index": 5,
  "value": "0000000000000000000000000000000000000000000000000000000000000008"
}
Enter fullscreen mode Exit fullscreen mode

Ah!

Observe que os irmãos são os mesmos nas provas antes e depois!

Lembre-se que quando atualizamos uma folha, ela apenas muda os nós no caminho de Merkle da folha e, como por definição o caminho de Merkle da folha não inclui nenhum irmão, as provas antes e depois têm os mesmos irmãos!

Se olharmos mais a fundo, o fato de ambas as provas fornecerem os mesmos irmãos e índice, verificar ambas as provas provam que modificamos apenas a folha com índice I:

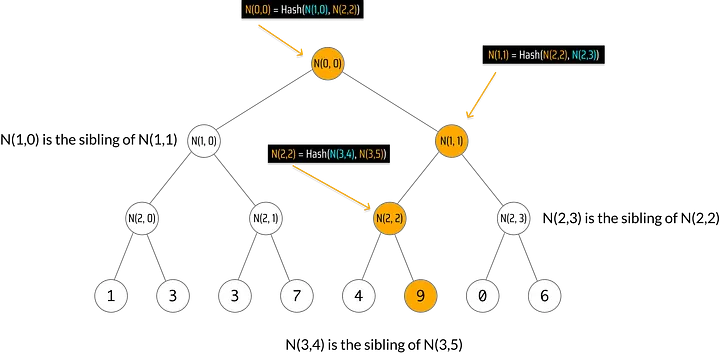Apenas os nós laranja no caminho de Merkle mudam, então os irmãos (brancos) permanecem os mesmos

Portanto, nossa prova de Merkle delta precisa fornecer:

  1. O índice da folha (o mesmo para as provas antes e depois).
  2. Os irmãos da folha (o mesmo para as provas antes e depois).
  3. O valor antigo da folha (antes da mudança).
  4. A raiz antiga da árvore (a raiz da árvore antes da alteração).
  5. O novo valor da folha (após alterarmos o valor da folha).
  6. A nova raiz da árvore (após alterarmos o valor da folha).

Podemos implementar uma função getDeltaMerkleProof para fazer isso para nós:

class MerkleTree {
  // ...
  getDeltaMerkleProof(level, index, newValue){
    // calcula a raiz da folha no índice I
    const oldLeafProof = this.getMerkleProof(level, index);
    // calcula a raiz deMerkle a partir da prova, substituindo o valor da folha pelo novo valor
    const newRoot = computeMerkleRootFromProof(oldLeafProof.siblings, index, newValue);

    // retorna os dados da prova antiga e da nova prova
    return {
      index: index,
      siblings: oldLeafProof.siblings,

      oldRoot: oldLeafProof.root,
      oldValue: oldLeafProof.value,

      newRoot: newRoot,
      newValue: newValue,
    }
  }
}
Enter fullscreen mode Exit fullscreen mode

Para verificar a prova de Merkle delta, podemos dividir os dados das provas de Merkle delta em newProof e oldProof que compartilham os mesmos irmãos/índice e verificar as provas usando nossa função VerifyMerkleProof existente:

function verifyDeltaMerkleProof(deltaMerkleProof){
  // divide a prova de Merkle delta em uma prova de Merkle antes e depois, reutilizando os mesmos irmãos e índices
  const oldProof = {
    // reutilizar os mesmos irmãos tanto para os antigos quanto para os novos
    siblings: deltaMerkleProof.siblings, 
    // reutilizar o mesmo índice para o antigo e o novo
    index: deltaMerkleProof.index,

    root: deltaMerkleProof.oldRoot,
    value: deltaMerkleProof.oldValue,
  };

  const newProof = {
    // reutilizar os mesmos irmãos tanto para os antigos quanto para os novos
    siblings: deltaMerkleProof.siblings, 
    // reutilizar o mesmo índice para o antigo e o novo
    index: deltaMerkleProof.index,

    root: deltaMerkleProof.newRoot,
    value: deltaMerkleProof.newValue,
  };
  return verifyMerkleProof(oldProof) && verifyMerkleProof(newProof);
}
Enter fullscreen mode Exit fullscreen mode

Vamos combinar isso e ver se funciona:

const shajs = require("sha.js"); // instala o npm --salva sha.js

function hash(leftNode, rightNode) {
  return shajs("sha256")
    .update(leftNode + rightNode, "hex")
    .digest("hex");
}
function getSiblingNode(level, index){
  // se o nó for a raiz, ele não terá irmãos
  if(level === 0){
    throw new Error("a raiz nao tem um irmao")
  }else if(index % 2 === 0){
    // se o nó for par, seu irmão está no índice+1
    return {level: level, index: index+1};
  }else{
    // se o nó for ímpar, seu irmão está no índice-1
    return {level: level, index: index-1};
  }
}
function getMerklePathOfNode(level, index){
  const merklePath = [];
  for(let currentLevel=level;currentLevel>0;currentLevel--){
    merklePath.push({
      level: currentLevel,
      index: index,
    });
    index = Math.floor(index/2);
  }
  return merklePath;
}
class MerkleTree {
  constructor(height, leaves){
    this.height = height;
    this.leaves = leaves;
  }
  N(level, index){
    if(level === this.height){
      // se level == height, o nó é uma folha, portanto, basta retornar o valor do nosso conjunto de dados
      return this.leaves[index];
    }else{
      // se o nó não for uma folha, use nossa definição:
      // N(level, index) = Hash(N(level+1, index*2), N(level+1, index*2+1))
      return hash(
        this.N(level+1, 2*index),
        this.N(level+1, 2*index+1),
      );
    }
  }
  getRoot(){
    // o nó N(0,0) é sempre o nó raiz
    return this.N(0,0);
  }
  getMerkleProof(level, index){

    // obtém o valor do nó folha
    const leafValue = this.N(level, index);

    // obter os níveis e índices dos nós no caminho de Merkle da folha    const merklePath = getMerklePathOfNode(level, index);

    // obter os níveis e índices dos irmãos dos nós no caminho de Merkle
    const merklePathSiblings = merklePath.map((node) => {
      return getSiblingNode(node.level, node.index);
    });

    // obter os valores dos nós irmãos
    const siblingValues = merklePathSiblings.map((node) => {
      return this.N(node.level, node.index);
    });

    return {
      root: this.getRoot(), // a raiz que afirmamos ser a raiz de nossa árvore
      siblings: siblingValues, // os irmãos do caminho de Merkle de nossa folha
      index: index, // o índice de nossa folha
      value: leafValue, // o valor de nossa folha
    };
  }
  getDeltaMerkleProof(level, index, newValue){
    // calcula a raiz da folha no índice I
    const oldLeafProof = this.getMerkleProof(level, index);
    // calcular a raiz de Merkle a partir da prova, substituindo o valor da folha pelo novo valor
    const newRoot = computeMerkleRootFromProof(oldLeafProof.siblings, index, newValue);

    // retorna os dados da prova antiga e da nova prova
    return {
      index: index,
      siblings: oldLeafProof.siblings,

      oldRoot: oldLeafProof.root,
      oldValue: oldLeafProof.value,

      newRoot: newRoot,
      newValue: newValue,
    }
  }
}
function computeMerkleRootFromProof(siblings, index, value){
  // iniciar nosso caminho de nó Merkle no nó folha
  let merklePathNodeValue = value;
  let merklePathNodeIndex = index;

  // seguimos o caminho de Merkle da folha até a raiz, calculando os nós do caminho de Merkle usando os irmãos fornecidos à medida que avançamos sozinhos
  for(let i=0;i<siblings.length;i++){
    const merklePathNodeSibling = siblings[i];

    if(merklePathNodeIndex%2===0){
      // se o índice atual do nó em nosso caminho de Merkle for par:
      // * merklePathNodeValue é o nó esquerdo,
      // * merklePathNodeSibling é o nó direito,
      // * o valor do nó pai é hash(merklePathNodeValue, merklePathNodeSibling)
      merklePathNodeValue = hash(merklePathNodeValue, merklePathNodeSibling);
    }else{
      // se o índice atual do nó em nosso caminho de Merkle for ímpar:
      // * merklePathNodeSibling é o nó esquerdo,
      // * merklePathNodeValue é o nó direito,
      // * o valor do nó pai é hash(merklePathNodeSibling, merklePathNodeValue)
      merklePathNodeValue = hash(merklePathNodeSibling, merklePathNodeValue);
    }

    // Usando nossa definição, o nó pai de nosso nó de caminho é  N(level-1, floor(index/2))
    merklePathNodeIndex = Math.floor(merklePathNodeIndex/2);
  }
  return merklePathNodeValue;
}
function verifyMerkleProof(proof){
  return proof.root === computeMerkleRootFromProof(proof.siblings, proof.index, proof.value);
}
function verifyDeltaMerkleProof(deltaMerkleProof){
  // dividir a prova de Merkle delta em uma prova de Merkle antes e depois, reutilizando os mesmos irmãos e índices
  const oldProof = {
    // reutilizar os mesmos irmãos tanto para os antigos quanto para os novos
    siblings: deltaMerkleProof.siblings, 
    // reutilizar o mesmo índice para o antigo e o novo
    index: deltaMerkleProof.index,

    root: deltaMerkleProof.oldRoot,
    value: deltaMerkleProof.oldValue,
  };

  const newProof = {
    // reutilizar os mesmos irmãos tanto para os antigos quanto para os novos
    siblings: deltaMerkleProof.siblings, 
    // reutilizar o mesmo índice para o antigo e o novo
    index: deltaMerkleProof.index,

    root: deltaMerkleProof.newRoot,
    value: deltaMerkleProof.newValue,
  };
  return verifyMerkleProof(oldProof) && verifyMerkleProof(newProof);
}
function example6(){
  const height = 3;
  const leaves = [
    "0000000000000000000000000000000000000000000000000000000000000001", // 1
    "0000000000000000000000000000000000000000000000000000000000000003", // 3
    "0000000000000000000000000000000000000000000000000000000000000003", // 3
    "0000000000000000000000000000000000000000000000000000000000000007", // 7
    "0000000000000000000000000000000000000000000000000000000000000004", // 4
    "0000000000000000000000000000000000000000000000000000000000000009", // 9
    "0000000000000000000000000000000000000000000000000000000000000000", // 0
    "0000000000000000000000000000000000000000000000000000000000000006", // 6
  ];
  const tree = new MerkleTree(height, leaves);

  const deltaMerkleProofOfN3_5 = tree.getDeltaMerkleProof(3,5, "0000000000000000000000000000000000000000000000000000000000000008");
  console.log("[EX_6] delta merkle proof of changing N(3,5) from 9 to 8:\n" + JSON.stringify(deltaMerkleProofOfN3_5, null, 2));
  console.log("[EX_6] verify delta merkle proof: "+verifyDeltaMerkleProof(deltaMerkleProofOfN3_5));
}

example6();
Enter fullscreen mode Exit fullscreen mode

A execução deste código imprime:

[EX_6] delta merkle proof of changing N(3,5) from 9 to 8:
{
  "index": 5,
  "siblings": [
    "0000000000000000000000000000000000000000000000000000000000000004",
    "deb2a27a00dbc46e3a59096a8d07d2b97f950158886411ff6a9c9ab9623dada6",
    "2f4d3e941b602c50347af3f5c809a28737c27c7ce460e77b10739875ef957aa7"
  ],
  "oldRoot": "e74ae221cf067dc8e88195f5b30bfda60dc224a8cd5554bc6345c87ad8c6f925",
  "oldValue": "0000000000000000000000000000000000000000000000000000000000000009",
  "newRoot": "99ba6856d11cd514be35ed291e86ae7957ec43d6b83270f32aaa50a8a25dc5cc",
  "newValue": "0000000000000000000000000000000000000000000000000000000000000008"
}
[EX_6] verify delta merkle proof: true
Enter fullscreen mode Exit fullscreen mode

Sucesso! Nós já inventamos os conceitos centrais por trás das árvores de Merkle, provas de Merkle e provas de Merkle delta.

Mais importante, com essa intuição, podemos usar nosso entendimento completo de como as provas de Merkle funcionam para implementar variantes dessas provas para criar armazenamentos de dados úteis e eficientes para nosso protocolo de camada 2.

No próximo tutorial, construiremos um banco de dados de árvore de Merkle eficiente para grandes árvores de Merkle esparsas, escreveremos uma árvore de Merkle anexada apenas que usa apenas armazenamento O(log(N)) e investigaremos algumas variantes de prova de Merkle que nos permitem mesclar árvores e provar o estado histórico.

Graças aos nossos patrocinadores OAS & QED, você pode seguir a OAS no twitter @OASNetwork

Sobre o autor — siga @cmpeq no twitter ou confira minha página sobre.

Artigo escrito por Carter Feldman. Traduzido por Marcelo Panegali.

Top comments (0)


Leia o próximo

devaraujo profile image

Criar Contrato Inteligente de Crowdfunding usando Solidity e Linguagem Golang

Adriano P. Araujo -

s4mp41xao profile image

Participe do Build NFT GAMES e aprenda a criar seu próprio jogo NFT.

Samuel Paixão -

isabelacnehme profile image

Teste de Hardhat Sem Conhecer JavaScript

Isabela Curado Nehme -

isabelacnehme profile image

Explorando Provas de Conhecimento Zero com Solidity e Muito Mais! 🕵️‍♂️🔐

Isabela Curado Nehme -