Esse artigo é uma tradução de Jesus Rodriguez feita por Diogo Jorge. Você pode encontrar o artigo original aqui.
Um dos maiores avanços na criptografia moderna pode ter um impacto profundo nos protocolos blockchain.
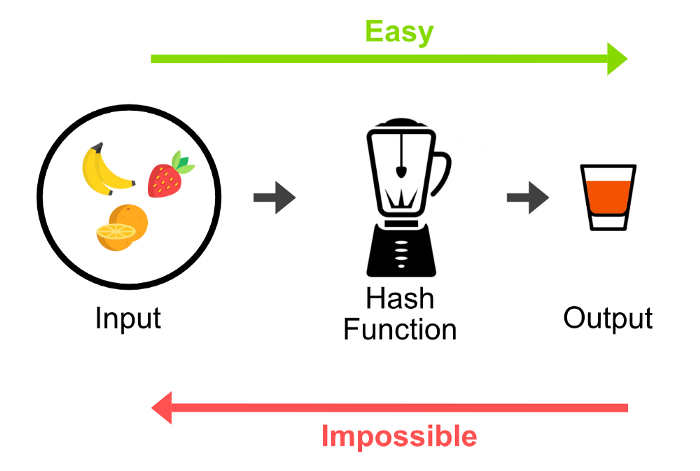
Fonte: https://saividyanand.blogspot.com/2020/05/what-is-cryptographysymmetric.html
A criptografia está no centro de muitos protocolos blockchain. Da tradicional prova de trabalho (PoW) às abordagens modernas L2, como ZK-rollups, muitos métodos criptográficos avançados fornecem a base dos tempos de execução e protocolos da blockchain. Consequentemente, há uma questão onipresente sobre a robustez da segurança de qualquer arquitetura blockchain. Ingenuamente, assumimos que as implementações criptográficas da blockchain que sobreviveram a ataques complexos são inerentemente seguras, mas isso está longe de ser uma prova empírica. Existe uma maneira melhor de verificar a robustez dos algoritmos de segurança. As respostas parecem estar em um novo artigo que acaba de ganhar o “Melhor Concurso de Documentos de Pesquisa em Segurança Cibernética” da Agência de Segurança Nacional (NSA) causando muito barulho na comunidade de pesquisa em criptografia.
Intitulado “On One-way Functions and Kolmogorov Complexity” , o artigo fornece uma resposta para um dos problemas do quincentenário em criptografia. O problema em questão está relacionado à existência de uma construção matemática chamada “funções unidirecionais” que pode provar se um método como uma prova de conhecimento zero em uma blockchain L2 é criptograficamente seguro.
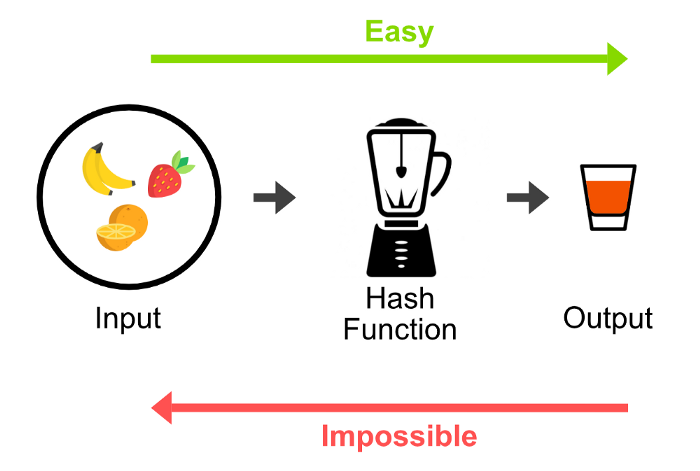
A essência da criptografia moderna depende da criação de cifras nos dados com a esperança de que eles permaneçam seguros. No entanto, como podemos ter certeza de que eles estão protegidos? A resposta teórica a essa pergunta veio na década de 1970, quando os criptógrafos apresentaram a ideia de funções unidirecionais, que são funções matemáticas fáceis de calcular, mas difíceis de reverter. Para ilustrar como funcionam as funções unidirecionais, pense se alguém lhe pedir para multiplicar dois grandes números primos como 485144 e 999983. Chegar ao número 485.135.752.552 como resposta pode dar algum trabalho, mas temos um método para fazer isso. Agora vamos pegar a pergunta inversa e começar com o número e tentar determinar seus fatores primos. Essa é uma tarefa monumentalmente mais difícil. Esta é a essência das funções unidirecionais.
A base das técnicas criptográficas usadas em blockchains de L1 e L2 tem como premissa a existência de funções unidirecionais. Se existe uma função unidirecional para um determinado problema, ela é criptograficamente protegida e, caso contrário, é provável que seja vulnerável a ataques diferentes. No entanto, até agora tem sido quase impossível provar a existência de funções unidirecionais. Em seu artigo, pesquisadores da Universidade de Cornell encontraram uma resposta traçando paralelos com uma área obscura da ciência da computação.
Entre na Complexidade de Kolmogorov
A resposta proposta no artigo de pesquisa de Cornell afirma essencialmente que a existência de funções unidirecionais está relacionada a outro problema fundamental da ciência da computação conhecido como complexidade de Kolmogorov (KC). A teoria KC está relacionada com a complexidade das cadeias de números. Se você for apresentado a dois números grandes 66666666666666666666 e 123948109102912, você não pode provar qual é “mais aleatório” do que o outro, mas intuitivamente você acha que o segundo número é mais complexo de gerar. Essa foi a ideia usada pelo matemático soviético Andrey Kolmogorov para iniciar uma nova teoria em complexidade computacional. Essencialmente, a teoria KC define a complexidade de uma string numérica como o comprimento do programa mais curto possível que produz a string como saída. Voltando ao nosso exemplo,

Crédito da imagem: Revista Quanta
A teoria KC é bem mais complexa, mas espero que você tenha entendido a ideia central. Por décadas, a teoria KC se tornou a base de muitas áreas da ciência da computação, mas não tem sido tão relevante na criptografia. Isso foi até que a equipe de pesquisa de Cornell tirou um coelho da cartola e mostrou que a existência de funções unidirecionais está relacionada ao KC de um determinado problema. Em termos simples, se um problema é um complexo KC, então existe uma função unidirecional e, se não for, provavelmente não existe.
Essa simples declaração pode se tornar uma das descobertas mais revolucionárias da criptografia moderna.
O que isso significa para o mundo Blockchain?
O artigo de Cornell fornece uma maneira empírica de avaliar a robustez das técnicas criptográficas usadas em blockchains L1 e L2. Isso é particularmente relevante considerando o surgimento de tempos de execução L2 baseados em técnicas criptográficas, como computações multipartidárias seguras ou provas de conhecimento zero. Determinar se um algoritmo é complexo KC é fundamentalmente mais simples do que determinar a existência de funções unidirecionais. É verdade que esse problema se expande muito além do ecossistema blockchain, mas, se estamos falando sobre a construção dos trilhos de um novo sistema financeiro, a robustez criptográfica é um recurso fundamental.