Nos bastidores do protocolo zkSNARK Groth16 (parte 1)
Zero Knowledge Proofs (ZKP) é um conceito que tem atraído muita atenção na indústria de blockchain. Muitos, inclusive eu, a certa altura, veem isso como uma misteriosa “caixa preta”. Neste artigo e nas séries subsequentes, compartilharei o que aprendi sobre um dos protocolos ZKP e um em particular - zkSNARK Groth16.
Esta série será complementada com código funcional, que pode ser acessado em GitHub.
Mas primeiro, vamos estabelecer o que queremos dizer com provas de conhecimento zero. ZKP é um protocolo que normalmente envolve duas partes: Alice e Bob. Aqui está a essência: Alice quer convencer Bob de que ela possui uma informação específica sem realmente revelar quaisquer detalhes dessa informação a ele. Além disso, forjar tal prova é quase impossível, a menos que você tenha um computador quântico no bolso.
Para ilustrar isto com um exemplo, imagine que Alice precisa de partilhar provas da existência da sua conta bancária com uma organização governamental. Usando o ZKP, ela pode provar que possui uma conta bancária sem revelar qual banco ela usa ou a quantia em dinheiro em sua conta.
Outra aplicação potencial do ZKP é na verificação de processos computacionais específicos. Digamos que exista um software que realiza testes de análise forense. Com o ZKP, podemos garantir que estes testes foram genuinamente realizados, os seus resultados podem ser verificados e é quase impossível falsificá-los.
zkSNARK
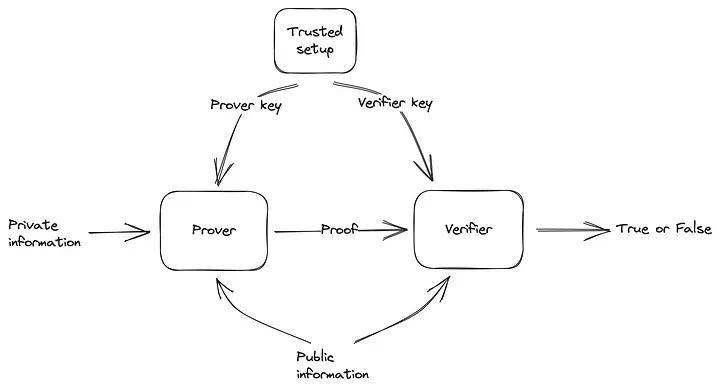
Aqui está uma imagem que mostra a configuração do zkSNARK. Ao contrário de outros protocolos ZKP, como STARK e Bulletproofs, o zkSNARK requer terceiros durante a fase de inicialização. Este terceiro fornece ao comprovador e ao verificador suas respectivas chaves. \
Os blocos “comprovador” e “verificador” são programas que residem nos lados do provador (Alice) e do verificador (Bob), respectivamente. Um aspecto interessante do protocolo SNARK Groth16 é que o verificador pode ser integrado a um contrato inteligente implantado na blockchain Ethereum. Isto introduz um novo conjunto de aplicações na plataforma e simplifica a adoção da tecnologia blockchain na vida cotidiana. \
Vamos começar com o comprovador.
Comprovador
Como mencionei anteriormente, tanto o comprovador quanto o verificador são programas, cada um executado e hospedado por partes diferentes. Comparando os dois em termos de requisitos computacionais e complexidade de código, o provador é sem dúvida o mais sofisticado dos dois. Consequentemente, o tempo de execução tenderá a ser maior do lado do provador.
O tempo de execução do comprovador dependerá em grande parte da complexidade do programa, sendo escalonado linearmente como O(n). Em contraste, a complexidade do código do verificador permanece constante em O(1), garantindo tempos de verificação estáveis, independentemente da afirmação que o comprovador tenta provar.
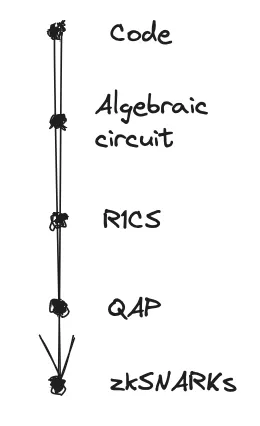
Você deve ter visto o diagrama abaixo, que descreve as etapas envolvidas na geração de provas. Fornecerei uma visão geral das duas primeiras etapas sem me aprofundar muito, enquanto as etapas subsequentes serão ilustradas com exemplos de código e explicações.
Código
Como o ZKP existe no domínio da criptografia, isso implica na limitação de um conjunto de programas que podem ser implementados usando protocolos ZKP. Vamos considerar um exemplo onde o comprovador precisa executar o seguinte programa:
def compute(x, y):
a = 5*x**3 + x**2
b = 4*x**2*y**2 + 13*x*y**2 - 10*y
if y == 0:
return a
else:
return a + b
Em geral, esta função pode não parecer particularmente significativa, mas para os nossos propósitos é suficiente. Como você pode ver, a função contém uma instrução “if”. Isto deve sugerir a possibilidade de que o código possa conter outras construções de programação, como loops, por exemplo. Contudo, no caso de SNARKs, os cálculos devem ser limitados. Isto significa que o número de iterações deve ser conhecido antecipadamente, e o número de parâmetros, bem como o seu tamanho, também deve ser predeterminado.
Se você está questionando a variedade e a complexidade das tarefas que podem ser realizadas pelo zkSNARK, aqui está um pequeno trecho de código que escrevi alguns anos atrás: https://gist.github.com/tarassh/cb2a48966fa5db3c803cba134d00b0e4. Esta é uma versão adaptada usada para calcular a métrica SSIM do codec de vídeo h264.
Voltando ao nosso exemplo: como mencionado anteriormente, o ZKP opera no domínio da criptografia e, consequentemente, no domínio da matemática. Assim, este código deve ser convertido em uma equação aritmética. Existem diversas bibliotecas capazes de realizar esta conversão, incluindo:
- Zokrates: o código é escrito em uma linguagem semelhante ao Python.
- Circom: usa sua própria linguagem específica de domínio.
- Pequin do Pepper-Project: utiliza uma linguagem semelhante à C, semelhante à essência fornecida acima.
Ignorando os detalhes de como o código é convertido em uma equação, o exemplo fornecido anteriormente pode ser representado pela seguinte equação:
out = 5*x**3 - 4*x**2*y**2 + 13*x*y**2 + x**2 - 10*y
Ou:
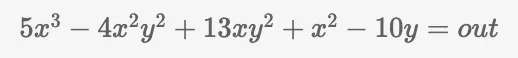
Quanto maior a complexidade do seu cálculo, mais longa será a equação resultante. Em última análise, esta equação serve como base para a construção de um circuito algébrico.
Circuito Algébrico
Agora, precisamos dividir nossa equação em operações sequenciais menores, seguindo as seguintes regras:
- Cada operação deve consistir em dois parâmetros de entrada e um parâmetro de saída.
- Somente variáveis (como x e y no nosso caso) podem servir como parâmetros de entrada. As constantes devem estar associadas a um dos parâmetros de entrada.
- Várias operações de adição podem ser consolidadas em uma única variável. Além disso, a subtração pode ser representada como uma adição: a-b é equivalente a a+(-b).
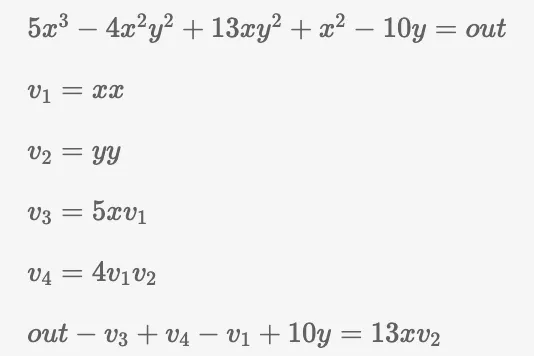
Portanto, nossa equação pode ser dividida em 5 restrições. Aqui está uma lista de etapas do que aconteceu aqui:
Primeiro, podemos substituir x² com uma nova variável, v1, e aceita dois parâmetros de entrada: x e x. Agora a equação ficará a seguir:
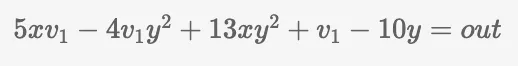
Em seguida, podemos substituir e² com uma nova variável, v2, e a equação ficará assim:
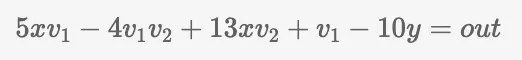
E assim por diante... Notavelmente, se você escolher um par diferente de parâmetros de entrada, digamos em 1=xy, você introduzirá duas restrições adicionais. O objetivo principal aqui é identificar o menor número de restrições que possam representar com precisão esta equação.
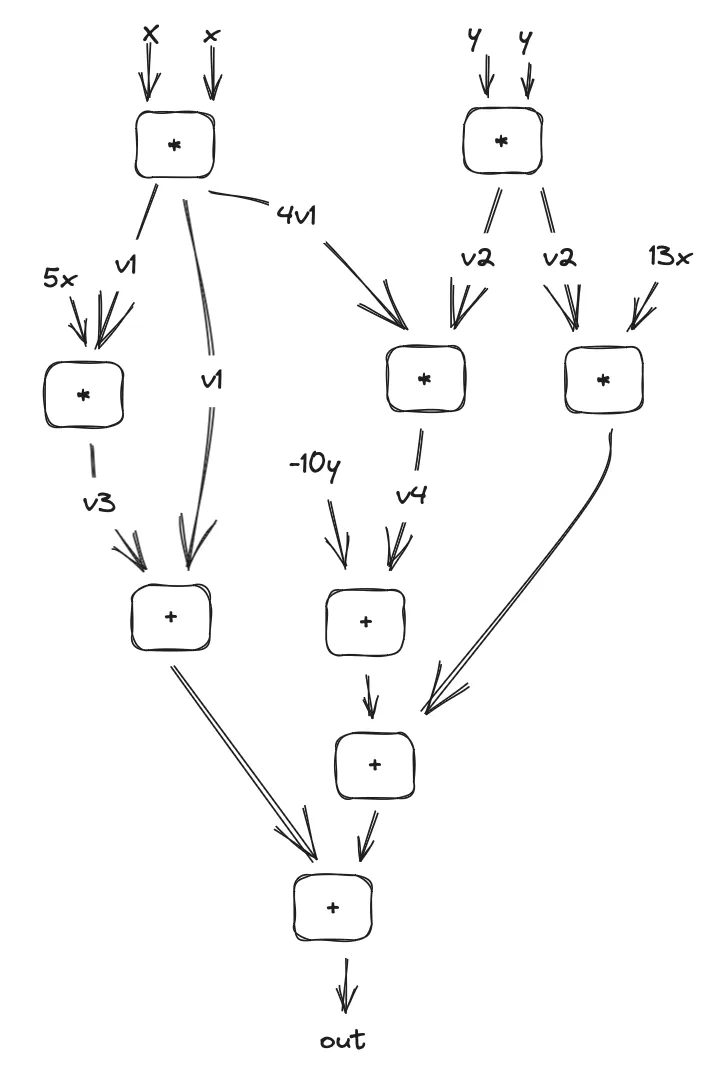
Esquematicamente, isso pode ser visualizado como um circuito. É importante observar que as operações de adição podem ser consolidadas, conforme exemplificado pela fórmula out=1×(em3+em1-10e-em4+em5), onde em 5=13xv2 é uma nova variável. No entanto, por uma questão de otimização e pelas razões explicadas no artigo subsequente, a fórmula deve assumir a seguinte forma:
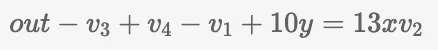
Parte 2:
Nos bastidores do protocolo zkSNARK Groth16 (parte 2)
No artigo anterior, cobrimos brevemente os dois primeiros componentes do protocolo SNARK: o código e o algébrico…
Referências:
- https://www.rareskills.io/post/rank-1-constraint-system
- https://eprint.iacr.org/2016/260.pdf
- https://github.com/tarassh/zkSNARK-under-the-hood/blob/main/groth16.ipynb
Este artigo foi escrito por Crypto Fairy e traduzido por Diogo Jorge. O artigo original pode ser encontrado aqui.

