Na parte anterior, construímos nossa primeira configuração de provador-verificador, o que é bastante interessante. No entanto, ainda faltam alguns componentes importantes.
Nos bastidores do protocolo zkSNARK Groth16 (parte 4)
Até agora, conseguimos comprimir a avaliação do trabalho do provador em três pontos na curva elíptica: A, B e C. Aqui está uma breve recapitulação de como era no início:
- O R1CS foi representado como uma multiplicação de matrizes Lw×Rw=Cw.
- Então, graças ao homomorfismo, o R1CS foi transformado no QAP na forma polinomial, dado por_ U(τ)×V(τ)=W(τ)+H×T(τ)_.
- Agora, está representado na forma de pontos de curva elíptica: A×B=C
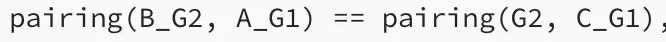
A×B=C
α, β
Embora a estrutura seja preservada, devemos introduzir restrições a esta equação para realizá-la totalmente como um zkSNARK. Quando o verificador recebe pontos A, B, e C, eles não podem determinar se esses pontos são resultados genuínos de uma avaliação ou apenas um truque do provador. Por esta mesma razão, precisamos introduzir dois parâmetros adicionais, α (alfa) e β (beta). Estes parâmetros devem ser fornecidos por um agente de configuração confiável:
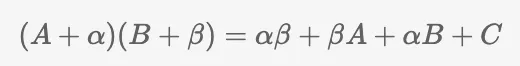
Quando expandimos os colchetes à esquerda, certos termos se anulam com os termos do lado direito, fazendo com que a equação volte à sua forma original. Contudo, o que isso significa para o provador e verificador?
Agora, o provador deve calcular (A + α), (B + β), βA, αB, eC. Enquanto isso, o verificador terá que calcular o emparelhamento αβ, também conhecido como “multiplicação” (valores fornecidos pela configuração confiável) e verifique se a equação é válida. É crucial observar que os valores alfa e beta devem ser criptografados pelo agente de configuração, semelhante ao valor tau discutido no artigo anterior. Como tanto o provador quanto o verificador recebem alfa e beta, deixá-los sem criptografia ainda permitiria que o provador enganasse o verificador.
Você deve estar se perguntando por que o provador precisa calcular tantos valores. Não seria suficiente que o verificador fosse fornecido com A, B, C do provador, e α, e β da configuração confiável e, em seguida, realizar uma verificação simples? Existem algumas considerações que ainda não abordamos, mas vamos raciocinar com as informações que temos no momento. Em primeiro lugar, pretendemos construir o verificador on-chain, que apresenta certas limitações.
Neste contexto específico, a prova torna-se considerável, abrangendo 10 parâmetros, cada um com 32 bytes de comprimento. Isto leva a custos de execução substanciais. Em segundo lugar, desejamos que a prova seja sucinta (S em SNARK), tão compacta quanto possível. Portanto, sim, o provador tem uma carga computacional aumentada.
Devemos revisitar as matrizes Lp, Rp e Op, que contém os coeficientes polinomiais. É necessário calcular β×Lp e α×Rp. Eventualmente, esses cálculos produzirão os valores βA e αB. O agente de configuração é responsável por calcular esses parâmetros.
Agora vamos codificar a parte do agente de configuração (alternativamente você pode encontrar o código aqui):
def evaluate_poly_list(poly_list, x):
results = []
for poly in poly_list:
results.append(poly(x))
return results
def print_evaluation(name, results):
print(f'\n{name} polynomial evaluations:')
for i in range(0, len(results)):
print(f'{name}_{i} = {results[i]}')
def to_poly(mtx):
poly_list = []
for i in range(0, mtx.shape[0]):
poly_list.append( galois.Poly(mtx[i][::-1]) )
return poly_list
def print_poly(name, poly_list):
print(f'\n{name} polynomials:')
for i in range(0, len(poly_list)):
print(f'{name}_{i} = {poly_list[i]}')
print("Setup phase")
print("-"*10)
print("Toxic waste:")
alpha = FP(2)
beta = FP(3)
tau = FP(20)
print(f"α = {alpha}")
print(f"β = {beta}")
print(f"τ = {tau}")
beta_L = beta * Lp
alpha_R = alpha * Rp
K = beta_L + alpha_R + Op # preimage of [βA + αB + C]
Kp = to_poly(K)
print_poly("K", Kp)
print("K evaluations:")
K_eval = evaluate_poly_list(Kp, tau)
print([int(k) for k in K_eval])
Fase de configuração
Lixo tóxico:
α = 2
β = 3
τ = 20
K polynomials:
K_0 = 0
K_1 = 20976232752179305421319472172538221959858849217065366246044112345468483141633x^4 + 9120101196599698009269335727190531286895151833506680976540918411073253539840x^3 + 11856131555579607412050136445347690672963697383558685269503193934395229601794x^2 + 1824020239319939601853867145438106257379030366701336195308183682214650707966x + 1
K_2 = 4560050598299849004634667863595265643447575916753340488270459205536626769924x^4 + 16416182153879456416684804308942956316411273300312025757773653139931856371669x^3 + 17328192273539426217611737881662009445100788483662693855427744981039181725872x^2 + 5472060717959818805561601436314318772137091100104008585924551046643952123623x + 151
K_3 = 9120101196599698009269335727190531286895151833506680976540918411073253539840x^4 + 7296080957279758407415468581752425029516121466805344781232734728858602831879x^3 + 12768141675239577212977070018066743801653212566909353367157285775502554955742x^2 + 14592161914559516814830937163504850059032242933610689562465469457717205663813x + 21888242871839275222246405745257275088548364400416034343698204186575808495577
K_4 = 12768141675239577212977070018066743801653212566909353367157285775502554955776x^4 + 10944121435919637611123202872628637544274182200208017171849102093287904247814x^3 + 9120101196599698009269335727190531286895151833506680976540918411073253539824x^2 + 10944121435919637611123202872628637544274182200208017171849102093287904247827x + 21888242871839275222246405745257275088548364400416034343698204186575808495611
K_5 = 11856131555579607412050136445347690672963697383558685269503193934395229601792x^4 + 12768141675239577212977070018066743801653212566909353367157285775502554955783x^3 + 20976232752179305421319472172538221959858849217065366246044112345468483141607x^2 + 20064222632519335620392538599819168831169334033714698148390020504361157787691x + 21888242871839275222246405745257275088548364400416034343698204186575808495595
K_6 = 17328192273539426217611737881662009445100788483662693855427744981039181725697x^4 + 12768141675239577212977070018066743801653212566909353367157285775502554955774x^3 + 4560050598299849004634667863595265643447575916753340488270459205536626769931x^2 + 9120101196599698009269335727190531286895151833506680976540918411073253539823x + 9
K_7 = 2736030358979909402780800718157159386068545550052004292962275523321976061952x^4 + 12768141675239577212977070018066743801653212566909353367157285775502554955778x^3 + 8208091076939728208342402154471478158205636650156012878886826569965928185851x^2 + 20064222632519335620392538599819168831169334033714698148390020504361157787657x + 21888242871839275222246405745257275088548364400416034343698204186575808495613
K evaluations:
[0, 3876, 321276, 21888242871839275222246405745257275088548364400416034343698204186575808469777, 21888242871839275222246405745257275088548364400416034343698204186575808440081, 21888242871839275222246405745257275088548364400416034343698204186575808450720, 16644, 21888242871839275222246405745257275088548364400416034343698204186575808484958]
Agora o agente precisa criptografar os parâmetros:
from py_ecc.optimized_bn128 import multiply, G1, G2, add, pairing, neg, normalize, eq
# G1[α]
alpha_G1 = multiply(G1, int(alpha))
# G1[β]
beta_G1 = multiply(G1, int(beta))
# G1[τ^0], G1[τ^1], ..., G1[τ^d]
tau_G1 = [multiply(G1, int(tau**i)) for i in range(0, T.degree)]
# G1[βU0(τ) + αV0(τ) + W0(τ)], G1[βU1(τ) + αV1(τ) + W1(τ)], ..., G1[βUd(τ) + αVd(τ) + Wd(τ)]
k_G1 = [multiply(G1, int(k)) for k in K_eval]
# G1[τ^0 * T(τ)], G1[τ^1 * T(τ)], ..., G1[τ^d-1 * T(τ)]
target_G1 = [multiply(G1, int(tau**i * T_tau)) for i in range(0, T.degree - 1)]
# G2[α]
beta_G2 = multiply(G2, int(beta))
# G2[τ^0], G2[τ^1], ..., G2[τ^d-1]
tau_G2 = [multiply(G2, int(tau**i)) for i in range(0, T.degree)]
print("Trusted setup:")
print("-"*10)
print(f"[α]G1 = {normalize(alpha_G1)}")
print(f"[β]G1 = {normalize(beta_G1)}")
print(f"[τ]G1 = {[normalize(point) for point in tau_G1]}")
print(f"[k]G1 = {[normalize(point) for point in k_G1]}")
print(f"[τT(τ)]G1 = {[normalize(point) for point in target_G1]}")
print(f"\n[β]G2 = {normalize(beta_G2)}")
print(f"[τ]G2 = {[normalize(point) for point in tau_G2]}")
Configuração confiável:
----------
[a]G1 = (1368015179489954701390400359078579693043519447331113978918064868415326638035, 991811005130217158508040260331970277456 5515993150576347155970296011118125764)
[b]G1 = (3353031288059533942658390886683067124040920775575537747144343083137631628272, 193215337665523688609465524374805154414 16830039777911637913418824951667761761)
[τ]G1 = [(1, 2), (18947110137775984544896515092961257947872750783784269176923414004072777296602, 1229208503769329158608364496643 4670280746730626861846747147579999202931064992), (1626219947120579441354494782674593865413210475263758669204832971331159039701 1, 13296900385261935021718889695689394625708483652039722230815936262285054528714), (216036000706896757664384706613459547824193 55 034652174505468210225883925863279, 15787091953565760722773063158476721787069408761080596737736006929439659379800 015254050 70663195453841654293855276471519589821575313643995787424. 3417460412)]
[k]G1 = [(0, 0), (17518925876389381914155930110408777142106130111113028150026931997812097774535, 8858392472586588859720780881006 689049064823023738566495968587324881339689331), (7776932200273552787128105306335292200128839089213803200158363828327183775433, 1676473267286376034272794912591089409235063853265136908465687242866588965033), (9255362000568086969426581910999695218767488354 0 11423148343055923150063610530, 19663255005511524857343047157430517662352787346134121583487236661223935168532), (4584923233296 35 0927122616402897357895248802996295595163135244549277455848652, 52423078528682697259449017062969413272086449244737515824764 011 23626838714022), (16055450244558982737197017116370443036836369038269239292860030068216908828776, 16459830096784505310827542 4194 19419268816240069809368541804931193116745432653), (92078746459698017673729321254256450874696097141080915625962792199931425 37032, 21595782772050531164058871317405782630067754355442908985935623343510342105362), (17872882827220769851948196436082177999996849 857792425314560729399495672579835, 14652213235113259189221731167852105559603034798387944587962349555346774854421)]
[τT(τ)]G1 = [(1641247283492879903468444805169804215277964208279225379119694118848884481979, 1873324532856297253506807250581161 2 803902036184072974454572123739995203670419), (1282524939337382483469274134339301655621870987447481453798307725808867601190, 1 55 39182012162102815636574710752557587640625547182202465638914992086098498248), (1947009009880180826230649135264243588041513836 657 5553697569183294142349316803, 21283889500356371386534994908069309335293143510390960327225612194996849127112), (102729485734 1653 2171977932623710258063324920576107343417279327107779961629108,187852823669808014650450779923664292744739680900471298121 71188 476045329716662)]
[b]G2 = ((2725019753478801796453339367788033689375851816420509565303521482350756874229, 72731651027999311117158714715503779097 3 5733521218303035754523677688038059653) 4722006818841961785324909313781880061366718538693995380805373202866))
[t]G2 = [(10857046999023057135944570762232829481370756359578518086990519993285655852781, 115597320329863871079910040213922857 83925812861821192530917403151452391805634). 367875863433681332203403145435568316851327593401208105741076214120093531)), ((658445688651052856222172029662443174632841252415 63 86210384049614268366928061, 13505823173380835868587575884635704883599421098297400455389802021584825778173, (510159176386055 456 9577488373372350852473588323930260132008193335489992486594, 1753783709436247797639692717863616216761517329092736300374379 4104 386247847571)), ((15315709620702712460485525966545043944570955016708868204420815750896718746085, 8198197634290639555322052 407476 232699891641457211856758911101094525731144652), (19804470431547976995467325770475378164766256111835164108366808772087600 898145, 4235451872741546336515947567132583436895052948569531554551940659752625222062) ) 15592044 28094 304399156219358984665346302412186219957044834017722538687643212)), ((7438610750340884426463248775247096468124645443296586 8797796 3153953325237344, 5808982581765237968275179275525571115489463112173520579009942912940231914163), (125753263562720009516) 45854762 614021668091710139241570303614619233551006506090, 600987892185797510428623699096699739721974087077140569734740259387 2065076583))]
Parte do provador:
print("\nProof generation:")
print("-"*10)
U = galois.Poly((w @ Lp)[::-1])
V = galois.Poly((w @ Rp)[::-1])
# G1[u0 * τ^0] + G1[u1 * τ^1] + ... + G1[ud-1 * τ^d-1]
A_G1 = evaluate_poly(U, tau_G1)
# G1[A] = G1[A] + G1[α]
A_G1 = add(A_G1, alpha_G1)
# G2[v0 * τ^0] + G2[v1 * τ^1] + ... + G2[vd-1 * τ^d-1]
B_G2 = evaluate_poly(V, tau_G2)
# G2[B] = G2[B] + G2[β]
B_G2 = add(B_G2, beta_G2)
# G1[h0 * τ^0 * T(τ)] + G1[h1 * τ^1 * T(τ)] + ... + G1[hd-2 * τ^d-2 * T(τ)]
HT_G1 = evaluate_poly(H, target_G1)
assert len(w) == len(k_G1), "Polynomial degree mismatch!"
# w0 * G1[k0] + w1 * G1[k1] + ... + wd-1 * G1[kd-1]
K_G1_terms = [multiply(point, int(scaler)) for point, scaler in zip(k_G1, w)]
K_G1 = K_G1_terms[0]
for i in range(1, len(K_G1_terms)):
K_G1 = add(K_G1, K_G1_terms[i])
C_G1 = add(HT_G1, K_G1)
print(f"[A]G1 = {normalize(A_G1)}")
print(f"[B]G2 = {normalize(B_G2)}")
print(f"[C]G1 = {normalize(C_G1)}")
print("-" * 10)
print("Verifier uses:")
print(f"[α]G1 = {normalize(alpha_G1)}")
print(f"[β]G1 = {normalize(beta_G1)}")
Geração de prova:
----------
[A]G1 = (1386024683863798223806715768494499062004541323940181712423964207525793364711, 140843658074195725477996606607942635995 385653032596678292076222071924134)
[B]G2 = ((2268131489099612700799057509317325492629365410973939712610009952960246451283, 54602028986188244498510046352089151618 45252587893842541197344609059159079041). 92494964230503385709419527449681227575755609196682056154158621712303733))
[C]G1 = (16949762960944359451850183815207514502115470096021213979561775521498090739408, 19195070842803981584459765300451665511 335687015857205049191967196163351934749)
----------
O verificador usa:
[a]G1 = (1368015179489954701390400359078579693043519447331113978918064868415326638035, 991811005130217158508040260331970277456 5515993150576347155970296011118125764)
[b]G1 = (3353031288059533942658390886683067124040920775575537747144343083137631628272, 193215337665523688609465524374805154414 16830039777911637913418824951667761761)
Quanto ao verificador, infelizmente, a biblioteca python não suporta adições para emparelhamentos, mas se fosse, poderia ser assim:
# A = A + α
# B = B + β
# C = βA + αB + C
# AB == αβ + [βA + αB + C]
assert pairing(B_G2, A_G1) == pairing(beta_G1, alpha_G1) + pairing(G2, C_G1)
Felizmente podemos fazer isso com solidity, mas temos que mover A*B para o lado direito:
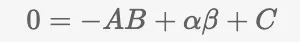
// SPDX-License-Identifier: UNLICENSED
pragma solidity ^0.8.9;
contract PairingTest {
// -A
uint256 constant aG1_x =
1386024683863798223806715768494499062004541323940181712423964207525793364711;
uint256 constant aG1_y =
21888102028181201026520927748650667146060315771644791066010745818423154284449;
// B
uint256 constant bG2_x1 =
2268131489099612700799057509317325492629365410973939712610009952960246451283;
uint256 constant bG2_x2 =
5460202898618824449851004635208915161845252587893842541197344609059159079041;
uint256 constant bG2_y1 =
21214978237453897862935673366579439999311734514850735211426933843714547507738;
uint256 constant bG2_y2 =
20956792494964230503385709419527449681227575755609196682056154158621712303733;
// alpha
uint256 constant alphaG1_x =
1368015179489954701390400359078579693043519447331113978918064868415326638035;
uint256 constant alphaG1_y =
9918110051302171585080402603319702774565515993150576347155970296011118125764;
// beta
uint256 constant betaG2_x1 =
2725019753478801796453339367788033689375851816420509565303521482350756874229;
uint256 constant betaG2_x2 =
7273165102799931111715871471550377909735733521218303035754523677688038059653;
uint256 constant betaG2_y1 =
2512659008974376214222774206987427162027254181373325676825515531566330959255;
uint256 constant betaG2_y2 =
957874124722006818841961785324909313781880061366718538693995380805373202866;
// C
uint256 constant cG1_x =
16949762960944359451850183815207514502115470096021213979561775521498090739408;
uint256 constant cG1_y =
19195070842803981584459765300451665511335687015857205049191967196163351934749;
// G2
uint256 constant G2_x1 =
10857046999023057135944570762232829481370756359578518086990519993285655852781;
uint256 constant G2_x2 =
11559732032986387107991004021392285783925812861821192530917403151452391805634;
uint256 constant G2_y1 =
8495653923123431417604973247489272438418190587263600148770280649306958101930;
uint256 constant G2_y2 =
4082367875863433681332203403145435568316851327593401208105741076214120093531;
function run(bytes memory input) public view returns (bool) {
// opcional, a pré-compilação também verifica isso e reverte (sem erro) se for falso, isso ajuda a restringir possíveis erros
if (input.length % 192 != 0) revert("Pontos devem ser multiplos de 6");
(bool success, bytes memory data) = address(0x08).staticcall(input);
if (success) return abi.decode(data, (bool));
revert("emparelhamento errado");
}
function verify() public view returns (bool) {
// -A * B + alpha * betta + C = 0
bytes memory points1 = abi.encode(
aG1_x,
aG1_y,
bG2_x2,
bG2_x1,
bG2_y2,
bG2_y1,
alphaG1_x,
alphaG1_y,
betaG2_x2,
betaG2_x1,
betaG2_y2,
betaG2_y1
);
bytes memory points2 = abi.encode(
cG1_x,
cG1_y,
G2_x2,
G2_x1,
G2_y2,
G2_y1
);
bytes memory points = abi.encodePacked(points1, points2);
return run(points);
}
}
Observação: Idealmente, os pontos A, B e C devem ser fornecidos como parâmetros de entrada para a função verify (verificar) . No entanto, por uma questão de simplicidade nesta demonstração, eles foram codificados. Para testemunhar isso em ação, você pode importar este contrato para o Remix Studio, compilá-lo e implantá-lo. Você observará que o resultado retorna verdadeiro.
Entradas (inputs) públicas e privadas
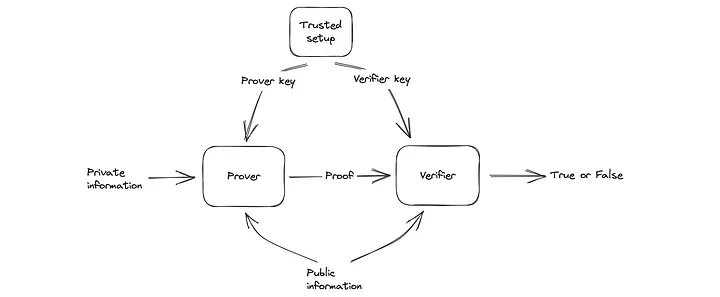
Se você se lembra do primeiro artigo, a imagem inicial introduziu um conceito que distingue entre informação pública e privada.
Nos bastidores do protocolo zkSNARK Groth16 (parte 1)
Os dados usados em nosso extenso exemplo são armazenados no vetor testemunha w com a seguinte estrutura:
- x, y, e out são os parâmetros de entrada e saída.
- _v_1 até _v_4 são resultados de computação intermediários.
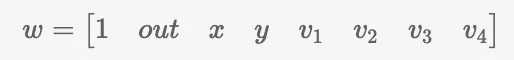
Até agora, esses dados eram tratados como privados. No entanto, neste exemplo, pretendo designar ‘1’ e ‘out’ como parâmetros públicos. Para conseguir isso, devemos dividir o vetor em duas partes.
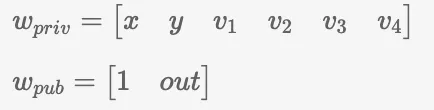
Observação: A sequência deve permanecer como [1, out] seguida de [x, y,…, v4]. Se houver necessidade de revelar outros dados (por exemplo, y e v4), você deve reorganizar essas entradas para que possam ser divididas em duas seções. Isso significa que as matrizes L, R, e O, pois o circuito aritmético também precisará de ajustes.
A seguir, precisamos ajustar os polinômios dividindo-os em duas partes. Vamos fazer um teste simples para ver se funciona.
def split_poly(poly):
coef = [int(c) for c in poly.coefficients()]
p1 = coef[-2:]
p2 = coef[:-2] + [0] * 2
return galois.Poly(p1, field=FP), galois.Poly(p2, field=FP)
u = U(tau)
v = V(tau)
_w = W(tau) # w taken by witness vector
ht = H(tau)*T_tau
U1, U2 = split_poly(U)
V1, V2 = split_poly(V)
W1, W2 = split_poly(W)
w1 = W1(tau)
w2 = W2(tau)
u1 = U1(tau)
u2 = U2(tau)
v1 = V1(tau)
v2 = V2(tau)
c = (beta * u2 + alpha * v2 + w2) + ht
k = (beta * u1 + alpha * v1 + w1)
assert (u + alpha) * (v + beta) == alpha * beta + k + c # deve ser igual
Dividimos a pré-imagem do ponto C, representado como_ βU+αV+W+HT_, em duas partes:
- c = [βU+αV+W+HT] — Este é o polinômio para a entrada privada.
- k = [
βU+αV+W] — Este é o polinômio para a entrada pública.
Para as pré-imagens de A e B, representadas como U+α and V+β respectivamente, nada mudou. A equação final ficará assim:
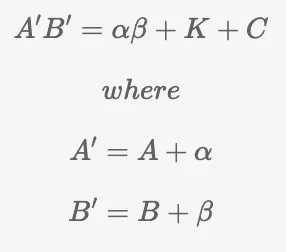
O provador fornecerá A', B', e C. Os valores de α e β são fornecidos ao verificador a partir da configuração confiável. O verificador é responsável por calcular o ponto K. O provador é obrigado a apresentar os valores [1 out] de forma não criptografada. Para criptografar esses valores, o verificador utilizará a multiplicação escalar da curva elíptica, e os pontos necessários para esta operação serão fornecidos pelo setup ([k1] * 1 + [k2] * out).
k_pub_G1, k_priv_G1 = k_G1[:2], k_G1[2:]
pub_input, priv_input = w[:2], w[2:]
print(f"[k_pub]G1 = {[normalize(point) for point in k_pub_G1]}")
print(f"[k_priv]G1 = {[normalize(point) for point in k_priv_G1]}")
print(f"pub_input = {pub_input}")
print(f"priv_input = {priv_input}")
[k_pub]G1 = [(0, 0), (17518925876389381914155930110408777142106130111113028150026931997812097774535, 8858392472586588859720780881006689049064823023738566495968587324881339689331)]
[k_priv]G1 = [(7776932200273552787128105306335292200128839089213803200158363828327183775433, 1676473267286376034272794912591089409235063853265136908465687242866588965033), (9255362000568086969426581910999695218767488354011423148343055923150063610530, 19663255005511524857343047157430517662352787346134121583487236661223935168532), (4584923233296350927122616402897357895248802996295595163135244549277455848652, 5242307852868269725944901706296941327208644924473751582476401123626838714022), (16055450244558982737197017116370443036836369038269239292860030068216908828776, 16459830096784505310827542419419419268816240069809368541804931193116745432653), (9207874645969801767372932125425645087469609714108091562596279219993142537032, 21595782772050531164058871317405782630067754355442908985935623343510342105362), (17872882827220769851948196436082177999996849857792425314560729399495672579835, 14652213235113259189221731167852105559603034798387944587962349555346774854421)]
pub_input = [ 1 104]
priv_input = [ 2 3 4 9 40 144]
Provador calcula sua parte:
K_priv_G1_terms = [multiply(point, int(scaler)) for point, scaler in zip(k_priv_G1, priv_input)]
K_priv_G1 = K_priv_G1_terms[0]
for i in range(1, len(K_priv_G1_terms)):
K_priv_G1 = add(K_priv_G1, K_priv_G1_terms[i])
C_G1 = add(HT_G1, K_priv_G1)
Prova do provador:
[A]G1 = (1386024683863798223806715768494499062004541323940181712423964207525793364711, 140843658074195725477996606607942635995 385653032596678292076222071924134)
[B]G2 = ((2268131489099612700799057509317325492629365410973939712610009952960246451283, 54602028986188244498510046352089151618 45252587893842541197344609059159079041). 92494964230503385709419527449681227575755609196682056154158621712303733))
[C]G1 = (3007959184562619447308758040351540166633693812660366965459472595743782653474, 216132861374015772001290673041609800597 29655631955179340440670659782625352184)
----------
O verificador usa:
[a]G1 = (1368015179489954701390400359078579693043519447331113978918064868415326638035, 991811005130217158508040260331970277456 5515993150576347155970296011118125764)
[b]G1 = (3353031288059533942658390886683067124040920775575537747144343083137631628272, 193215337665523688609465524374805154414 16830039777911637913418824951667761761)
[k_pub]G1 = [(0, 0), (17518925876389381914155930110408777142106130111113028150026931997812097774535, 8858392472586588859720780881006 689049064823023738566495968587324881339689331)]
Verificador:
// SPDX-License-Identifier: UNLICENSED
pragma solidity ^0.8.9;
contract PairingTest {
// A
uint256 constant aG1_x =
1386024683863798223806715768494499062004541323940181712423964207525793364711;
uint256 constant aG1_y =
140843658074195725477996606607942635995385653032596678292076222071924134;
// B
uint256 constant bG2_x1 =
2268131489099612700799057509317325492629365410973939712610009952960246451283;
uint256 constant bG2_x2 =
5460202898618824449851004635208915161845252587893842541197344609059159079041;
uint256 constant bG2_y1 =
21214978237453897862935673366579439999311734514850735211426933843714547507738;
uint256 constant bG2_y2 =
20956792494964230503385709419527449681227575755609196682056154158621712303733;
// alpha
uint256 constant alphaG1_x =
1368015179489954701390400359078579693043519447331113978918064868415326638035;
uint256 constant alphaG1_y =
9918110051302171585080402603319702774565515993150576347155970296011118125764;
// beta
uint256 constant betaG2_x1 =
2725019753478801796453339367788033689375851816420509565303521482350756874229;
uint256 constant betaG2_x2 =
7273165102799931111715871471550377909735733521218303035754523677688038059653;
uint256 constant betaG2_y1 =
2512659008974376214222774206987427162027254181373325676825515531566330959255;
uint256 constant betaG2_y2 =
957874124722006818841961785324909313781880061366718538693995380805373202866;
// C
uint256 constant cG1_x =
3007959184562619447308758040351540166633693812660366965459472595743782653474;
uint256 constant cG1_y =
21613286137401577200129067304160980059729655631955179340440670659782625352184;
// K1
uint256 constant k1G1_x =
0;
uint256 constant k1G1_y =
0;
// K2
uint256 constant k2G1_x =
17518925876389381914155930110408777142106130111113028150026931997812097774535;
uint256 constant k2G1_y =
8858392472586588859720780881006689049064823023738566495968587324881339689331;
// public input
uint256 one = 1;
uint256 out = 104;
uint256 constant G2_x1 =
10857046999023057135944570762232829481370756359578518086990519993285655852781;
uint256 constant G2_x2 =
11559732032986387107991004021392285783925812861821192530917403151452391805634;
uint256 constant G2_y1 =
8495653923123431417604973247489272438418190587263600148770280649306958101930;
uint256 constant G2_y2 =
4082367875863433681332203403145435568316851327593401208105741076214120093531;
uint256 constant Q =
21888242871839275222246405745257275088696311157297823662689037894645226208583;
struct G1Point {
uint256 x;
uint256 y;
}
struct G2Point {
uint256 x1;
uint256 x2;
uint256 y1;
uint256 y2;
}
function add(
G1Point memory p1,
G1Point memory p2
) public view returns (G1Point memory r) {
(bool ok, bytes memory result) = address(6).staticcall(
abi.encode(p1.x, p1.y, p2.x, p2.y)
);
require(ok, "g1add failed");
(uint256 x, uint256 y) = abi.decode(result, (uint256, uint256));
r = G1Point(x, y);
}
function mul(
G1Point memory p,
uint256 scalar
) public view returns (G1Point memory r) {
(bool ok, bytes memory result) = address(7).staticcall(
abi.encode(p.x, p.y, scalar)
);
require(ok, "g1mul falhou");
(uint256 x, uint256 y) = abi.decode(result, (uint256, uint256));
r = G1Point(x, y);
}
function negate(G1Point memory p) internal pure returns (G1Point memory) {
// O primo q no campo base F_q para G1
if (p.x == 0 && p.y == 0) return G1Point(0, 0);
return G1Point(p.x, Q - (p.y % Q));
}
function run(bytes memory input) public view returns (bool) {
// opcional, a pré-compilação também verifica isso e reverte (sem erro) se for falso, isso ajuda a restringir possíveis erros
if (input.length % 192 != 0) revert("Pontos devem ser um múltiplo de 6");
(bool success, bytes memory data) = address(0x08).staticcall(input);
if (success) return abi.decode(data, (bool));
revert("Emparelhanmento errado");
}
function emulate() public view returns(bool) {
G1Point memory A = G1Point(aG1_x, aG1_y);
G2Point memory B = G2Point(bG2_x1, bG2_x2, bG2_y1, bG2_y2);
G1Point memory C = G1Point(cG1_x, cG1_y);
uint256[2] memory input = [one, out];
return verify(A, B, C, input);
}
function verify(G1Point memory A, G2Point memory B, G1Point memory C, uint256[2] memory input) public view returns (bool) {
G1Point memory k1 = mul(G1Point(k1G1_x, k1G1_y), input[0]);
G1Point memory k2 = mul(G1Point(k2G1_x, k2G1_y), input[1]);
G1Point memory K = add(k1, k2);
// -A * B + alpha * beta + C * 1(G2) + K * 1(G2) = 0
bytes memory points1 = abi.encode(
A.x,
negate(A).y,
B.x2,
B.x1,
B.y2,
B.y1,
alphaG1_x,
alphaG1_y,
betaG2_x2,
betaG2_x1,
betaG2_y2,
betaG2_y1
);
bytes memory points2 = abi.encode(
C.x,
C.y,
G2_x2,
G2_x1,
G2_y2,
G2_y1,
K.x,
K.y,
G2_x2,
G2_x1,
G2_y2,
G2_y1
);
bytes memory points = abi.encodePacked(points1, points2);
return run(points);
}
}
Reiterando: Em um cenário ideal, o contrato inteligente deveria aceitar pontos A,B,C e a 'entrada pública' como argumentos de função. No entanto, por uma questão de simplicidade nesta demonstração, todos os valores foram codificados. Estes podem ser facilmente verificados no Remix Studio ou aqui.
Há algumas coisas que precisam acontecer para implementar o protocolo Groth16. Abordaremos isso no próximo e último capítulo.
Nos bastidores do protocolo zkSNARK Groth16 (parte 6)
Referências:
- https://www.rareskills.io/post/r1cs-zkp
- https://eprint.iacr.org/2016/260.pdf
- https://github.com/tarassh/zkSNARK-under-the-hood/blob/main/groth16.ipynb
Este artigo foi escrito por Crypto Fairy e traduzido por Diogo Jorge. O artigo original pode ser encontrado aqui.

