Implementar Groth16 em sCrypt
Recentemente, implementamos os SNARKs-zk em sCrypt e o executamos no Bitcoin. Mais especificamente, implementamos o verificador do algoritmo Groth16, que permite que uma prova zero-knowledge seja verificada diretamente on-chain. Este artigo mergulha em alguns dos detalhes, lançando luz sobre como implementar eficientemente outras técnicas criptográficas avançadas em Bitcoin.

Emparelhamentos bilineares em curvas elípticas
Groth16 aprecia extremamente pequeno tamanho de prova e verificação rápida. O emparelhamento é a parte mais cara do algoritmo do verificador Groth16. Nós escolhemos o emparelhamento Ate otimizado, já que sua eficiência tem sido demonstrada na prática.
Nós o implementamos sobre a curva elíptica de emparelhamento amigável BN256 (também conhecida como ALT_BN128 e BN254). Utilizamos a BN256, pois ela é 1) suportada por ferramentas ZKP populares como ZoKrates e Circom; 2) compatível com outras blockchains, tais como Ethereum.
O algoritmo de Miller é usado para calcular eficientemente o emparelhamento Ate otimizado. Em um nível elevado, ele consiste de duas partes:
- Loop de Miller: computar uma função intermediária dos dois pontos de entrada f(P, Q) repetidamente
- Exponenciação final: elevar f a uma grande potência c
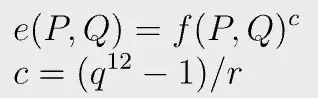

Redução a 3 emparelhamentos
O verificador precisa verificar se a seguinte equação é válida.
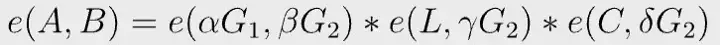
Equação 2
Tuple (tupla) (A, B, C) é a prova, (α, β, ϒ, δ) é a chave de verificação e L é derivada dos inputs públicos. Temos 4 emparelhamentos no total. Observamos que α e β são conhecidos na configuração, então nós precomputamos o segundo emparelhamento e substituímos α e β por ele, como parte da chave de verificação, economizando um emparelhamento.
Uma única exponenciação final
Eq. 1 pode ser reescrita assim:
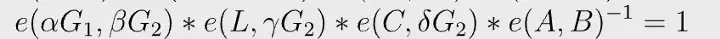
Por sua vez, pode ser escrita da seguinte forma, uma vez que e é bilinear e podemos retirar o expoente (-1) do parênteses.
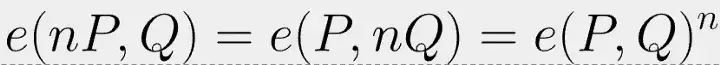
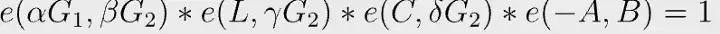
Juntando a Eq. 2, temos:
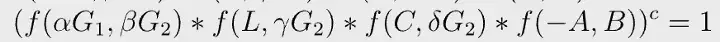
Em vez de calcular a exponenciação final 4 vezes, que fica computacionalmente intenso, só temos que fazer isso uma vez no final.
Desenrolando o Loop
Em sCrypt/Script, todos os ramos if estão incluídos em uma transação e incorrem em taxas de transação, independentemente de serem executadas mais tarde ou não. No loop de Miller, sᵢ é conhecido no momento da compilação. Nós desenrolamos o loop e evitamos a ramificação nas linhas 5 e 7.
Extensão de rotação do campo
O emparelhamento computacional de dois pontos diretamente requer aritmética de curva elíptica sobre o campo de extensão Fq¹², que é extremamente complicada e ineficiente. Usamos uma twist (torção) para mapeá-lo para Fq², melhorando drasticamente a eficiência. Por favor, consulte este artigo para uma explicação mais detalhada.
Resumo
Após todas essas otimizações, conseguimos reduzir o tamanho do Script de emparelhamento em 100X para 5MB. Estamos explorando mais otimizações para reduzi-lo ainda mais. A versão completa do código pode ser encontrada em GitHub.
Tradicionalmente, o objetivo de otimizar um programa é minimizar seu uso de CPU e/ou memória. No Bitcoin, onde a taxa de transação é proporcional ao tamanho de uma transação contendo o Script, o objetivo é minimizar o tamanho do script. Como otimizar face a este objetivo é um tópico interessante e aberto, digno de uma pesquisa inovadora.
Esse artigo foi escrito por sCrypt e traduzido por Fátima Lima. O original pode ser lido aqui.

