Introdução
Circom é uma linguagem para circuitos aritméticos usados para gerar provas de conhecimento zero. O compilador Circom é um compilador da linguagem Circom escrito em Rust que cria o arquivo R1CS. O Circom foi criado pelo projeto de código aberto Iden3.
Definição
O circuito é uma representação lógica do problema computacional usando polinômios.
Testemunha é a atribuição de sinais ao circuito.
Os sinais são as variáveis.
O Rank-1 Constraint System (R1CS) é o conjunto de restrições que descreve o circuito. Exemplo: A * B + C = 0
Restrição é criar um programa que restrinja as entradas fornecidas em um determinado intervalo.
Os componentes funcionam como funções, e definimos as entradas dos componentes apenas uma vez. Quando todas as entradas do componente são definidas, a função é executada e podemos usar a variável de saída do componente.
Prova de conhecimento zero: uma pessoa, o provador, convence outra pessoa, o verificador, de que algo é verdadeiro sem revelar a entrada privada.
As provas de conhecimento zero não interativas (NIZK) são um tipo específico de provas de conhecimento zero em que o provador pode gerar a prova sem interação com o verificador.
ZK-SNARK (Zero Knowledge-Succinct ARguments of Knowledge) é a NIZK mais preferível. É um conjunto de protocolos de conhecimento zero não interativos que têm tamanho de prova sucinto e tempo de verificação sublinear.
Sucinto: a prova real fornecida ao verificador é uma prova muito menor do que a proposição original. Isso é ser sucinto.
O ZK roll up agrega muitas transações fora da cadeia e gera uma única prova, usando o ZK-SNARK para reduzir o tamanho dos dados. A prova é enviada na cadeia e verificada na cadeia. O ZK roll up também atualiza a árvore de merkle da conta na cadeia.
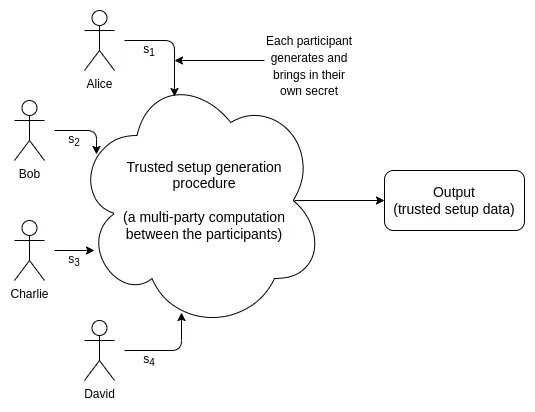
Configuração de criptografia confiável: a configuração confiável gera um dado que deve ser usado na operação de criptografia. Uma cerimônia de configuração confiável é um procedimento para gerar os dados.
Algoritmo ZK-Snark: Groth16 (Filecoin, Tornado.cash, Old Zcash) é o mais utilizado, seguido por Plonk (zkSync, Mina) e Halo (New Zcash).
Sequência conceitual do ZK roll up:
- Verificar informações do remetente:
hash da chave pública do remetente, calcular a raiz da merkle.
- Criar assinatura da nova transação:
criar um hash da chave pública do remetente e do destinatário, com o valor da transação;
usar EdDSA para assinar e verificar o hash.
- Atualizar o novo saldo do remetente com o valor da transação:
calcular a nova raiz de merkle;
verificar a nova raiz.
- Verificar as informações do receptor:
hash da chave pública do receptor, calcular a raiz da merkle.
- Atualizar o novo saldo do receptor com o valor da transação
calcular a nova raiz de merkle;
verificar a nova raiz.
- Publicar a nova raiz na cadeia.
Etapas para fazer o rollup do zk:
As etapas a seguir são executadas no código de exemplo em https://github.com/victoryeo/circom_rollup.
É necessário instalar o Circom e o Snarkjs em seu computador.
- Compile o circuito
circom rollup.circom --r1cs --wasm --sym --c
Ele gera arquivos wasm e cpp, além de restrições R1CS.
2.a Gere a testemunha com o webassembly
cd rollup_js
node generate_witness.js rollup.wasm ../input.json witness.wtns
2.b Gere a testemunha com cpp
cd rollup_cpp
make
./rollup ../input.json witness.wtns
A etapa 2 atribui um valor a cada sinal e gera o arquivo de testemunha do circuito. Isso é equivalente a executar o circuito.
3. Execute a configuração confiável
Usando powers of tau (configuração confiável de várias partes):
snarkjs powersoftau new bn128 18 pot12_0000.ptau -v
Inicialmente, uso bn128 12 e recebo este erro:
[snarkJS: circuito muito grande para essa cerimônia de potência de tau. 39582*2 > 2**12]
snarkjs powersoftau contribute pot12_0000.ptau pot12_0001.ptau --name=”First contribution” -v
snarkjs powersoftau prepare phase2 pot12_0001.ptau pot12_final.ptau -v
snarkjs groth16 setup rollup.r1cs pot12_final.ptau rollup_0000.zkey
A etapa acima leva de 30 minutos a 1 hora para ser executada no meu laptop.
`snarkjs zkey contribute rollup_0000.zkey rollup_0001.zkey --name=”1st Contributor Name” -v`
rollup_0000.zkey é a chave antiga.
rollup_0001.zkey é a nova chave.
zkey é uma chave de conhecimento zero que combina chaves de comprovação e de verificação.
snarkjs zkey export verificationkey rollup_0001.zkey verification_key.json
O procedimento acima gera a chave de verificação no formato json.
4. Gere uma prova ZK
snarkjs groth16 prove rollup_0001.zkey witness.wtns proof.json public.json
São gerados dois arquivos, proof.json e public.json.
proof.json contém a chave de prova.
public.json contém os resultados públicos.
A etapa 4 gera uma prova ZK que contém as restrições definidas no circuito (deriva as restrições do circuito) e revela o resultado público.
5. Verificar uma prova ZK
snarkjs groth16 verify verification_key.json public.json proof.json
A etapa 5 obtém a saída pública, a chave de comprovação, a chave de verificação e decide o resultado da verificação.
A saída do console abaixo significa que a verificação foi bem-sucedida.
[INFO] snarkJS: OK!
Termos da biblioteca da Circom
Baby Jubjub: define um algoritmo que retorna uma curva elíptica a ser usada na prova ZK-SNARK, dado um número primo p. Ele é usado pelo ZK-SNARK. Baby Jubjub é uma curva de Edwards distorcida.
MiMC: define uma função hash para minimizar o tamanho do circuito.
MiMC sponge (esponja): cálculo do MiMC no modo esponja. O modo esponja é uma função que mapeia a entrada de comprimento variável para a saída de comprimento variável.
BN128: BN refere-se aos sobrenomes dos matemáticos que os descobriram em 2006, Paulo Barreto e Michael Naehrig. BN128 é uma curva elíptica de 128 bits.
EdDSA: algoritmo de assinatura digital da Edwards, o esquema de assinatura usado pelo ZK-SNARK.
Curva de Montgomery: outra curva elíptica.
Referências:
https://medium.com/coinmonks/hands-on-your-first-zk-application-70fe3a0c0d82
Fim.
Artigo escrito por Victor Yeo. A versão original pode ser encontrada aqui. Traduzido e adaptado por Dimitris Calixto.

