zkSNARKs para polinômios, passo a passo

######O autor agradece a Mak e à Unsplash pela imagem.
Introdução
Em nosso artigo anterior, introduzimos o conceito de SNARK e as propriedades básicas necessárias. Com o principal objetivo desta série de artigos em mente, ou seja, como construir zk-SNARKs para qualquer computação, introduzimos neste artigo a criação de um SNARK para comprovar o conhecimento de um polinômio. Faremos isso passo a passo, partindo de uma construção que não atenderá a todos os requisitos e chegando a um protocolo que será um SNARK de conhecimento zero "completo".
##ZK-SNARKs para polinômios
Construiremos um zk-SNARK passo a passo, começando de uma construção mais simples que não é um SNARK e, em seguida, aprimorando-o com novas técnicas até atingirmos nossos objetivos.
Primeiro passo: o lema de Schwartz-Zippel
Queremos criar um protocolo que permita que um provador P convença um verificador V do conhecimento de um polinômio específico de grau n com coeficientes em um campo finito F. Em outras palavras, P quer convencer V de que ele conhece um polinômio de forma
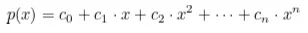
Vamos assumir que a_1, a_2, … , a_n ∈ F sejam as n raízes desse polinômio, portanto, p(x) pode ser escrito como
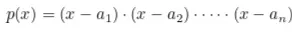
Suponhamos que V conheça d < n raízes do polinômio p(x).
Então podemos reformular nosso problema: agora P quer provar para V que ele conhece um polinômio h(x) tal que
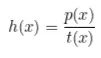
O polinômio t(x) será chamado de polinômio alvo. Observe que ele tem a forma
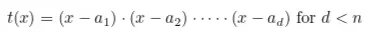
A primeira versão do nosso zk-SNARK é baseada no lema de Schwartz-Zippel: seja F um campo e f: F^m → F um polinômio multivariável de grau n. Então, para qualquer conjunto finito S ⊆ F:
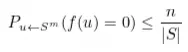
O que o lema mostra é que se escolhermos u ∈ Sm uniformemente ao acaso, a probabilidade de u ser um conjunto de raízes de f é no máximo n / |S|. Observe que essa probabilidade é pequena se considerarmos S como sendo o campo finito F. O tamanho do campo seria muito grande em comparação a n.
Pode parecer contraditório, mas este lema nos permite provar o conhecimento de um polinômio f. Não precisamos provar que conhecemos todos os coeficientes de p, mas apenas que sabemos como calcular o par (s, f(s)) para qualquer s ∈ F^m. O lema de Schwartz-Zippel fornece a eficiência necessária em nosso zk-SNARK.
Primeiro protocolo
Lembramos que P conhece o polinômio p(x) e V conhece d < n raízes de p(x) ou, equivalentemente, V conhece o polinômio alvo t(x). P também conhece t(x).
Nossa primeira abordagem é a seguinte:
V escolhe um valor aleatório s e calcula t = t(s). V envia s para P.
P calcula o polinômio h(x) usando o lema de Schwartz-Zippel.
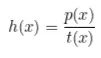
P então calcula os valores h = h(s) e p = p(s) e envia o par (h, p) para V.
V verifica se a igualdade p = t · h.
Este protocolo é correto, pois se P conhece o polinômio p(x), ele pode calcular h(x) e, portanto, P também pode calcular os valores h e p de modo que p = h · t. Por outro lado, este protocolo também é eficiente, devido ao lema de Schwartz-Zippel.
No entanto, este protocolo não é robusto, pois o provador pode calcular t = t(s) usando o polinômio alvo, mesmo que P não conheça p(x). Ele pode escolher um h aleatório e calcular p = h · t e enviar o par (h, p) para V, que aceitaria o par como válido.
Observamos que o ponto crítico que permite a P enganar V é que P conhece o ponto de avaliação s. Esse truque seria impossível se P pudesse avaliar p sem conhecer o ponto de avaliação s. Isso nos leva ao segundo passo: ofuscação homomórfica ou ocultação homomórfica.
Segundo passo: ofuscação homomórfica
Para tornar nosso protocolo robusto, precisamos ser capazes de avaliar um polinômio em um ponto, sem conhecer esse ponto.
Faremos isso com base na dificuldade do problema do logaritmo discreto. Para um computador clássico, o problema do logaritmo discreto é computacionalmente inviável: em um grupo cíclico G, de ordem p e gerado por um elemento g, determinar um elemento a tal que 𝛼 = ga (mod p) para um 𝛼 conhecido.
Assumindo a dificuldade do problema do logaritmo discreto, podemos ofuscar um valor a calculando 𝛼 = ga (mod p). Um receptor de 𝛼 sozinho não pode aprender o valor a. O ponto interessante dessa técnica é que a exponenciação tem algumas propriedades homomórficas:
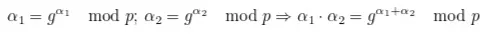
O produto de dois valores ofuscados é o mesmo que a ofuscação da adição dos valores associados em claro.
Se quisermos avaliar um polinômio
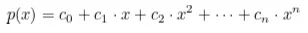
num ponto x = s, sem deixar o avaliador saber o ponto exato, precisamos ofuscar o polinômio inteiro:
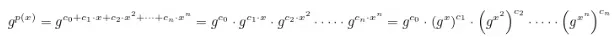
Também precisamos calcular as potências, de 1 até o grau do polinômio, de todos os valores ofuscados para x = r, ou seja:
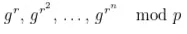
Observe que com todos esses elementos, agora podemos calcular a avaliação ofuscada do polinômio p em um ponto x = r. Na verdade:
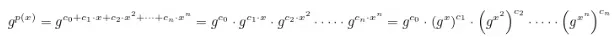
##Um exemplo de ocultação homomórfica
Vamos considerar o campo finito F = ℤ127 e g = 3, um gerador. Suponha que P conhece o polinômio p(x) = 4x² + 3x + 1 e que V quer que P avalie o polinômio no ponto x = 2 sem deixar P conhecer o ponto. Podemos fazer isso por meio das seguintes etapas:
V calcula todas as potências de x = 2 de 0 até o grau do polinômio, n = 2:
1.a. (3^1 \mod 127 = 3)
1.b. (3^2 \mod 127 = 9)
1.c. (3^4 \mod 127 = 81)
e envia o par (9, 81) para P.
P pode calcular a avaliação de p(x) em x = 2 sem conhecer o valor de x, de fato, usando as informações recebidas de V, ele pode calcular:
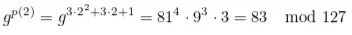
Segundo protocolo
Agora que sabemos como ofuscar pontos para que o provador possa avaliar o polinômio nesse ponto ofuscado, vamos melhorar o primeiro protocolo. Lembramos que P conhece o polinômio p(x) e V conhece d < n raízes de p(x) ou, equivalentemente, V conhece o polinômio alvo t(x). P também conhece t(x).
Nosso segundo protocolo é o seguinte:
V escolhe um valor aleatório s e calcula t = t(s).
V calcula e envia para P as seguintes potências:
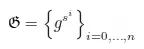
- P calcula o polinômio
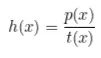
Usando os valores 𝔊, P calcula (g^p = g^{p(s)}) e (g^h = g^{h(s)}) usando as instruções do exemplo anterior.
P envia (g^p) e (g^h) para V.
V verifica se a seguinte identidade é verdadeira: (g^p = (g^h)^t)
Observe que a falha detectada no primeiro protocolo foi corrigida, mas este segundo protocolo ainda não é robusto. De fato, P ainda pode usar os valores (z_p) e (z_h) de forma que (z_p = (z_h)^t) e enviá-los para V como se fossem (g^p) e (g^h). P poderia fazer isso escolhendo um (r) aleatório, calculando (z_h = g^r) e definindo (z_p = (g^t)^r). O valor (z_p) pode ser calculado usando as potências ofuscadas enviadas por V.
Para evitar essa situação, precisamos garantir que (g^p) e (g^h) sejam calculados usando apenas as potências ofuscadas enviadas por V.
Terceiro passo: a suposição de conhecimento de expoente
Existe uma suposição comum ao definir um SNARK: consideremos um número primo (q) tal que (2q + 1) também seja um número primo. Consideremos (g) um gerador de (\mathbb{Z}_{2q + 1}). Dado (q), (g) e (g' = g^{\alpha}), queremos encontrar um par ((x, y)) tal que (x \neq g), (y \neq g') e (y = x^{\alpha}). A suposição de conhecimento de expoente (KEA) diz que a única maneira de encontrar o par ((x, y)) é tomando um valor (c \in \mathbb{Z}_q), calculando primeiro (x = g^c) e então tomando (y = (g')^c).
A KEA significa que se quisermos obter o par (x, y), a única forma de o fazer é conhecendo um expoente c tal que x = g^c. Por outras palavras, só podemos obter o par (x, y) com a propriedade KEA usando potências de g.
Usando a KEA, o protocolo abaixo garante que P retorne uma potência específica de (g), um gerador de um subgrupo multiplicativo, entregue por V:
V escolhe um valor aleatório (\alpha) e calcula (g' = g^{\alpha} \mod (2q + 1)).
V envia o par ((g, g')) para P e pede por um par ((b, b')) tal que ((b, b') = (g, g')).
P toma um valor (c) e calcula (b = g^c \mod (2q + 1)), (b' = (g')^c \mod (2q + 1)) e envia o par ((b, b')) para V.
V verifica se (b' = b^{\alpha} \mod (2q + 1)).
Observamos que, supondo que o problema do logaritmo discreto seja difícil, P não pode encontrar o valor de 𝛼 a partir do par (g, g'). Portanto, a única maneira de obter 𝛼 é computando todas as potências de g, conforme indicado pela KEA. Além disso, o protocolo acima está correto, pois
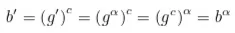
P usou a mesma potência c para g e g' e só pôde usar os valores fornecidos por V.
Terceiro protocolo:
Estamos prontos para construir um protocolo adequado que garantirá que o provador P produza potências do valor s no domínio ofuscado.
- V pega um valor aleatório s e calcula t = t(s).
- V pega um valor aleatório 𝛼 e calcula t(𝛼 - s).
- V calcula a seguinte série de valores ofuscados 𝔊 e os envia para P.
- V calcula a seguinte série de valores ofuscados
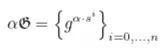
e os envia para P.
P calcula o polinômio h(x).
Usando 𝔊, P calcula p(s) e h(s) juntamente com g^p = g^{p(s)} e g^h = g^{h(s)}.
Usando 𝛼𝔊, P calcula p(s) e h(s) junto com g^{p'} = g^{p(𝛼 - s)}.
P envia g^p, g^h e g^{p'} para V.
V verifica se P fez os cálculos dos valores ofuscados usando apenas as informações que ele lhe enviou. Para isso, V verifica se g^p = g^{p'}.
V verifica se a seguinte identidade é válida: g^p = (g^h)^{t(s)}.
Esse protocolo agora atende às propriedades requeridas por um SNARK: é correto, é robusto e é eficiente. As próximas seções lidarão com a não interatividade e o conhecimento zero.
Observação: as etapas 6 e 7 no protocolo acima são realizadas de acordo com o exemplo de ocultação homomórfica.
Conhecimento Zero:
No protocolo apresentado até agora, os coeficientes ci do polinômio conhecido por P são muito específicos, e V poderia tentar aprender algumas informações sobre eles usando gp, gh e gp’ fornecidos por P. Portanto, para garantir que V não aprenda nada, P precisa ocultar esses valores.
A estratégia para ocultar os valores enviados por P segue as etapas usadas anteriormente: P escolhe um valor aleatório 𝛿 e o usa para ocultar os valores enviados na comunicação com V. Em vez de enviar g^p, g^h e g^{p’}, P calcula e envia (g^p)^𝛿, (g^h)^𝛿 e (g^{p’})^𝛿. Em seguida, V executa a verificação nos valores ocultos sob 𝛿.
De fato, o procedimento de verificação que V precisa executar ainda é válido com essa ocultação:
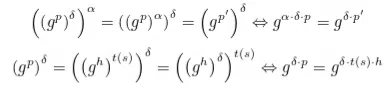
Portanto, para tornar o terceiro protocolo de conhecimento zero, substitui-se a etapa 8 para que P possa enviar os valores ofuscados.
Não Interatividade:
Os diferentes protocolos que apresentamos exigem a interação entre o provador e o verificador, pois a correção dos protocolos depende dos valores secretos s e 𝛼 escolhidos pelo verificador.
Se quisermos repetir qualquer um dos protocolos acima com outro verificador V', V' precisaria escolher novos valores s' e 𝛼'. Usar os valores gerados por V pode permitir que P trapaceie se ele se conspirar com V e V revela os valores s e 𝛼 para P.
Para evitar a situação acima, precisamos que nosso protocolo seja não interativo, e podemos alcançar isso usando parâmetros que sejam públicos, confiáveis e reutilizáveis. Isso pode ser alcançado ofuscando esses parâmetros usando um gerador g. No entanto, mesmo que as técnicas de ofuscação usadas sejam homomórficas, elas só permitem a adição de mensagens claras usando o produto de valores ocultos, mas não permitem realizar o produto de valores claros no domínio ofuscado, e esta etapa é crucial ao verificar a correção do polinômio e suas raízes.
Vamos introduzir emparelhamentos para resolver esse problema. Vamos lembrar que um emparelhamento tem a seguinte propriedade:
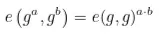
Essa propriedade permite verificar a igualdade de produtos no domínio ofuscado.
Portanto, para tornar nossos protocolos não interativos, o primeiro passo é pegar os valores secretos aleatórios s e 𝛼 e ofuscá-los: g^𝛼, 𝔊 e 𝛼𝔊.
Depois de calcular essas potências, podemos nos livrar dos valores secretos s e 𝛼 e transmitir seus valores ofuscados, conhecidos como String de Referência Comum (CRS ou Common Reference String). Os valores CRS geralmente são armazenados como:
- Chave de avaliação: (𝔊, 𝛼𝔊).
- Chave de verificação: (g^𝛼, g^{t(s)}).
O provador P usa os valores da chave de prova para avaliar o polinômio no domínio ofuscado, enquanto o verificador V usa a chave de verificação para verificar se a avaliação do polinômio em g^p, g^h, g^{p’} satisfaz:
Protocolo final: zk-SNARK para o conhecimento de um polinômio
Definimos agora um zk-SNARK para provar o conhecimento sobre um polinômio p(x) de grau n dado um polinômio alvo t(x).
Configuração de parâmetros:
Cada parte escolhe dois valores secretos s e 𝛼 aleatoriamente.
Cada parte calcula g^𝛼, 𝔊 e 𝛼𝔊.
Os valores s e 𝛼 são destruídos.
Um transmite a chave de avaliação (𝔊 e 𝛼𝔊).
Um transmite a chave de verificação g^𝛼, g^{t(s)}.
Prova:
Supondo que P conhece p(x), P calcula o polinômio h(x).
P avalia p(x) e h(x) e calcula gp(s) e gh(s) usando os valores contidos na chave de avaliação.
P calcula o valor g^{p(𝛼 · s)} usando a chave de avaliação.
P escolhe um valor aleatório 𝛿.
P transmite a prova π = (g^{𝛿 · p}, g^{𝛿 · h}, g^{𝛿 · p’}).
Verificação:
Supondo que V tem acesso a π = (g^{𝛿 · p}, g^{𝛿 · h}, g^{𝛿 · p’}), V verifica se
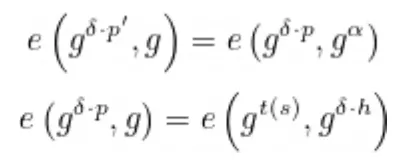
Conseguimos estabelecer um protocolo que satisfaz todas as propriedades necessárias na definição de um zk-SNARK: concisão (já que a prova verifica apenas um polinômio em um ponto), conhecimento zero e não interatividade (já que faz uso de um CRS).
Geração do CRS:
Zk-SNARKs podem ser tornados não interativos usando um conjunto de valores ocultos, conhecidos como a Common Reference String (CRS ou Cadeia de referência comum). Esses valores ocultos, que, no nosso caso, são da forma 𝔊 e 𝛼𝔊, vêm de valores secretos, s e 𝛼, que devem ser destruídos assim que os valores ocultos foram derivados. Observe que a geração do CRS é crítica, pois se delegarmos sua geração a um terceiro participante, todos precisam confiar que o participante destruirá os valores s e 𝛼. O terceiro participante representa um único ponto de falha.
Se quisermos evitar o único ponto de falha, precisamos de uma maneira distribuída de gerar o CRS, na qual um único participante honesto seja suficiente para garantir que os valores s e 𝛼 não possam ser recuperados.
Vamos usar o CRS para o SNARK que construímos em nosso exemplo anterior. Lembramos que, usando s e 𝛼 como segredos, precisamos calcular os valores ocultos e potências g^𝛼, 𝔊 e 𝛼𝔊.
Em nosso novo protocolo, substituiremos os valores s e 𝛼, gerados por um terceiro participante único, pelos valores s_{ABC} e 𝛼_{ABC} gerados por três usuários A, B e C. Estender o mecanismo para n usuários é direto.
O protocolo segue:
- O usuário A gera o par (sA, 𝛼A), calcula e transmite:
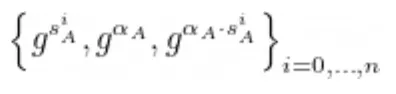
- O usuário B gera o par (sB, 𝛼B), calcula e transmite:
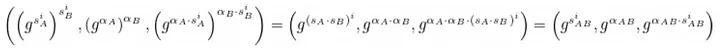
- B transmite:
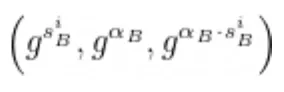
- C escolhe um par aleatório (sC, 𝛼C), calcula e transmite:
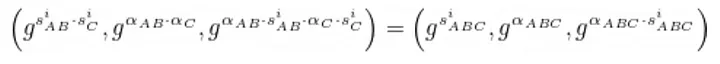
Este protocolo gera os valores ocultos para s_{ABC} = s_A · s_B · s_C e 𝛼_{ABC} = 𝛼_A · 𝛼_B · 𝛼_C sem que nenhum participante único conheça esse par de valores.
No entanto, precisamos de um protocolo que permita que os participantes verifiquem se esses valores ocultos foram calculados corretamente. Precisamos garantir que os valores gerados por cada usuário atendam aos requisitos, ou seja, o conjunto de valores 𝔊 são potências de gs, para o valor s de cada usuário, e que o conjunto 𝛼𝔊 foi calculado corretamente. Para fazer isso, verificamos se cada (g^s)^i é efetivamente a i-ésima potência de gs. Isso pode ser feito verificando se as seguintes igualdades são verdadeiras. Essa verificação é realizada por cada participante para todos os valores sU e 𝛼U associados a cada participante U:
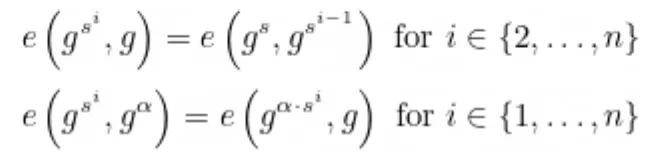
Esta não é a única verificação necessária. Também precisamos verificar se cada participante usa os valores corretos do participante anterior. Para fazer isso, cada participante usará parâmetros públicos ocultos de um usuário combinados com as saídas de outro participante. Por exemplo, C pode verificar os valores intermediários do CRS gerado por B, usando as informações do CRS de A, verificando o seguinte:
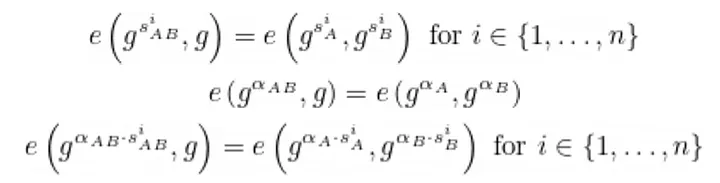
Conclusão:
Até agora, aprendemos como criar um SNARK, do zero e com todos os detalhes, para provar conhecimento de um polinômio. Em nosso próximo artigo, o último, estenderemos a construção acima para qualquer computação. Para fazer isso, introduziremos dois conceitos-chave: programas aritméticos quadráticos, QAPs, e sistemas de restrição de classificação-1, R1CS, embora este último não seja introduzido especificamente (aparecerá como uma mensagem subliminar).
Referências:
Jordi Herrera Joancomartí, Cristina Pérez Solà, _Criptografia avança_da. Lecture notes. Aberta da Catalunha, 2022.
Artigo escrito por Ramsès Fernàndez-València. Traduzido por Marcelo Panegali

