Compreensão da Teoria dos Grafos, Networkx e Conceitos Básicos de GNNs
 ######Foto de Omar Flores no Unsplash
######Foto de Omar Flores no Unsplash
O conceito de grafos é crucial em IA (Inteligência Artificial), mas é menos discutido. Minha nova série de artigos explora as Redes Neurais Gráficas (GNNs), o mais recente conjunto de Redes Neurais especialmente projetado para conjuntos de dados e problemas relacionados a grafos. Antes de mergulhar em algoritmos e códigos complexos, este artigo servirá como um ponto de partida para aqueles que estão começando a aprender sobre grafos. Este artigo abordará:
Conceitos básicos da Teoria dos Grafos (referenciados)
Introdução ao Networkx
O que são GNNs e por que usá-las?
Tipos de GNNs
Vetorização de Nós
Observação: já escrevi alguns posts sobre o Neo4j algum tempo atrás, então faremos referência aos artigos anteriores sempre que necessário para evitar repetição.
Vamos começar com:
Teoria dos Grafos
A teoria dos grafos é um ramo da matemática que estuda as relações entre objetos representados como nós (ou vértices) e as conexões entre eles representadas como arestas. Antes de avançarmos, presumo que entender o básico é importante. Meu artigo anterior deve ser um bom ponto de partida, abordando:
O que é um grafo?
Elementos básicos de um grafo (Nós, Vértices, Relacionamentos, etc.)
Tipos de Grafos
A série de artigos anterior estava mais focada no Neo4j (banco de dados de grafos), e todas as operações, como criação e análise de grafos, foram feitas usando o Neo4j. Mas para Redes Neurais Gráficas, usaremos códigos em Python, portanto, precisamos entender como criar esses grafos em Python. Para isso, usaremos o:
Networkx
O Networkx é um pacote em Python que nos ajuda a criar objetos de grafos em Python. Sem perder tempo, vamos começar instalando o Networkx:
pip3 install networkx
Em seguida, criaremos um grafo não direcionado de referência com alguns nós (nomes de cidades) e arestas (rotas de voo):
import networkx as nx
# grafo não direcionado (as arestas não têm direção)
G = nx.Graph()
# grafo direcionado (as arestas têm direção)
G = nx.DiGraph()
city_graph = [('Chennai', 'Delhi'), ('Mumbai', 'Chennai'), ('Delhi', 'Kolkata'),
('Delhi', 'Bangalore'), ('Chennai', 'Hyderabad'), ('Chennai', 'Jaipur')]
G.add_edges_from(city_graph)
nx.draw(G, with_labels=True)
O código é simples:
- Crie um grafo não direcionado ou direcionado usando
nx.Graph()ounx.DiGraph(). - Obtenha uma lista de tuplas representando arestas entre 2 nós.
- Adicione essas arestas ao objeto Grafo usando
add_edges_from(). - Visualize o grafo usando
draw(). Não se esqueça de mencionarwith_labels=Truepara mostrar os nomes dos nós.
 ######Direcionado (esquerda) e não direcionado (direita)
######Direcionado (esquerda) e não direcionado (direita)
Observação: existem muitas opções de formatação que você pode experimentar ao visualizar.
Vamos agora construir um grafo ponderado introduzindo uma relação 'distância' entre essas cidades:
import networkx as nx
import matplotlib.pyplot as plt
WG = nx.Graph()
city_graph = [('Chennai', 'Delhi', {'distance': 700}), ('Mumbai', 'Chennai', {'distance': 300}),
('Delhi', 'Kolkata', {'distance': 1000}), ('Delhi', 'Bangalore', {'distance': 20}),
('Chennai', 'Hyderabad', {'distance': 100}), ('Chennai', 'Jaipur', {'distance': 1200})]
WG.add_edges_from(city_graph)
# extrair rótulos para o atributo de distância que adicionamos acima
labels = nx.get_edge_attributes(WG, "distance")
# Desenhar o grafo
pos = nx.spring_layout(WG)
nx.draw(WG, pos, with_labels=True)
# Desenhar rótulos de aresta (pesos)
nx.draw_networkx_edge_labels(WG, pos, edge_labels=labels)
# Exibir o gráfico
plt.show()
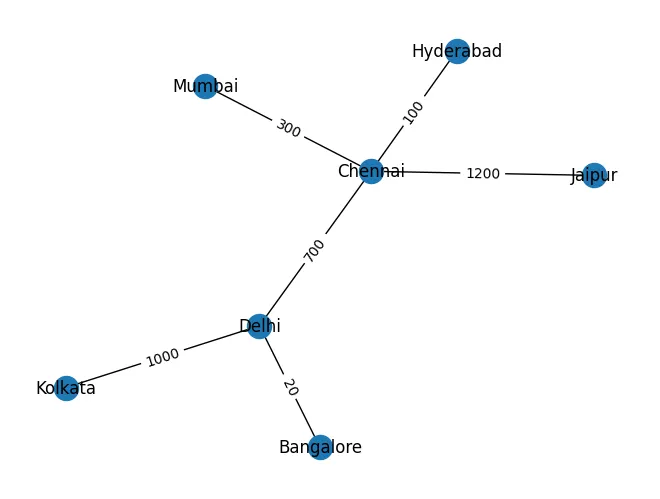
Isto requer um pouco de explicação. Ignorando as partes do trecho de código anterior na explicação.
Desta vez, estamos passando um objeto de dicionário como um elemento na tupla com o nome do relacionamento e seu valor. Você pode adicionar mais relacionamentos no dicionário.
Em seguida, extraímos 'propriedades de aresta' (qualquer relacionamento é uma propriedade da aresta e não dos nós) rótulos.
Obtenha um objeto de layout. Se não for feito, seu gráfico na visualização será mal formatado.
Desenhe o grafo passando esse objeto de layout.
Desenhe os rótulos das arestas passando o mesmo objeto de layout.
O Networkx pode ajudá-lo com muitos recursos integrados para Análise de Grafos, semelhante ao que fizemos no Neo4j. Vamos discutir alguns antes de nos aprofundarmos na Aprendizagem de Grafos e GNNs:
Grau: o número de arestas conectadas a um nó, representando seu nível de conectividade.
Centralidade de Grau: medida da importância relativa de um nó com base no número de suas conexões. Quanto mais arestas de um nó, maior o grau.
Centralidade de Intermediação: mede a importância de um nó dependendo de quantas vezes cada nó aparece nos caminhos mais curtos entre cada par de nós no grafo.
Conectividade: determina se um grafo está conectado ou consiste em componentes isolados.
Componentes Conectados: subgrafos disjuntos (não conectados) dentro de um grafo onde todos os nós estão conectados entre si.
Diâmetro: o mais longo dos caminhos mais curtos entre quaisquer dois nós, representando a distância máxima no grafo.
import networkx as nx
import matplotlib.pyplot as plt
# Criar um gráfico fictício
G = nx.Graph()
edges = [('A', 'B'), ('A', 'C'), ('B', 'D'), ('B', 'E'), ('C', 'F'), ('C', 'G')]
G.add_edges_from(edges)
# Centralidade de grau
degree_centrality = nx.degree_centrality(G)
print("Degree Centrality:")
for node, centrality in degree_centrality.items():
print(f"{node}: {centrality:.3f}")
# Centralidade de intermediação
betweenness_centrality = nx.betweenness_centrality(G)
print("\nBetweenness Centrality:")
for node, centrality in betweenness_centrality.items():
print(f"{node}: {centrality:.3f}")
# Grau
degree = dict(G.degree())
print("\nDegree:")
for node, deg in degree.items():
print(f"{node}: {deg}")
# Conectividade
is_connected = nx.is_connected(G)
print("\nIs Connected:", is_connected)
# Componentes
components = list(nx.connected_components(G))
print("\nConnected Components:", components)
# Diâmetro
diameter = nx.diameter(G)
print("\nDiameter:", diameter)
É hora de começarmos a falar sobre
Redes Neurais de Grafos
As GNNs (Redes Neurais Gráficas) são Redes Neurais especializadas projetadas especialmente para lidar com problemas de aprendizado de máquina relacionados a dados de grafo. Você pode considerá-las semelhantes ao que as CNNs (Redes Convolucionais Neurais) são para dados de imagem ou as LSTMs (Redes de Memória de Curto Prazo Longo) para dados de texto. Mas que tipos de problemas em grafos elas podem resolver? Alguns deles podem ser:
Classificação de Nós: prevê a categoria ou classe de um nó em um grafo, por exemplo, categorizando usuários ou itens online com base em características. O modelo é treinado em nós rotulados e em suas características para prever a classe de nós não rotulados.
Geração de Grafo: gera novos grafos com propriedades desejadas, comumente aplicados em descoberta de medicamentos para criar novas estruturas moleculares. O modelo é treinado em grafos existentes, aprendendo padrões e estruturas, e é então usado para gerar completamente novos grafos, não vistos anteriormente, para avaliação.
Classificação de Grafo: categoriza diferentes grafos em grupos predefinidos, frequentemente usado em biologia molecular para prever propriedades de estruturas moleculares no design de medicamentos. O modelo é treinado em grafos rotulados com atributos associados, permitindo categorizar novos grafos não vistos anteriormente.
Predição de Links: prevê links ausentes entre nós em um grafo, crucial para completar grafos de conhecimento (por exemplo, antecipar relacionamentos em uma rede social). O modelo é treinado para preencher conexões ausentes com base em estruturas de grafo existentes.
Mas esses problemas não podem ser resolvidos com algoritmos tradicionais de aprendizado de máquina?
Por que GNNs?
- No caso de algoritmos tradicionais de aprendizado de máquina, como Regressão Logística ou SVM, o modelo faz uma previsão com base nas características fornecidas sobre a amostra. No caso de grafos, além das informações disponíveis com o nó, muitas características podem ser derivadas de outros componentes, como nós ou arestas no grafo.
- Portanto, as GNNs, juntamente com as características disponíveis do nó, também derivam informações usando outros nós, arestas, relacionamentos, etc., e produzem uma representação latente de qualquer nó, tornando a representação muito mais abrangente e significativa.
- Essa representação final é agora uma combinação de características reais do nó + informações derivadas de outros componentes do grafo e não estão limitadas apenas às características reais fornecidas.
No entanto, essas informações extraídas de outros componentes diferem para diferentes GNNs.
Por exemplo, as Redes Convolucionais de Grafos (GCNs) usam uma operação de convolução (semelhante às CNNs sobre imagens) para extrair informações. Em uma GCN, a operação de convolução é geralmente aplicada de forma iterativa. Com cada iteração (ou camada na rede), a representação de um nó é atualizada com base em um bairro mais amplo. Inicialmente, a representação de um nó pode encapsular apenas informações de seus vizinhos imediatos. À medida que mais iterações são realizadas, a representação começa a incluir informações de um bairro cada vez maior.
Existem muitos tipos diferentes de GNNs. Alguns dos principais que discutirei em minhas próximas postagens são:
- Redes Convolucionais de Grafos (GCNs): utilizam camadas convolucionais para agregar e transformar informações de nós vizinhos, permitindo a aprendizagem eficaz de características em grafos.
- Redes de Atenção de Grafos (GATs): integram mecanismos de atenção para ponderar a importância de nós vizinhos de maneira diferente, aprimorando a agregação de características.
- Redes Neurais Recorrentes de Grafos (GRNNs): aplicam arquiteturas de redes neurais recorrentes a dados de grafo, capturando dependências sequenciais entre nós.
- Autoencoders de Grafos (GAEs): empregam uma estrutura de codificador-decodificador para aprender representações latentes de dados de grafo, frequentemente usados em tarefas de aprendizado não supervisionado, como incorporação.
- Redes Espaço-Temporais de Grafos: projetadas para lidar com grafos com dimensões espaciais e temporais, úteis para grafos dinâmicos como redes de tráfego.
- Redes Generativas de Grafos: visam gerar novas estruturas ou subgrafos, aprendendo a distribuição subjacente de dados de grafo.
Algoritmos de Vetorização de Nós
- Os algoritmos de vetorização de nós concentram-se em aprender representações vetoriais de baixa dimensionalidade dos nós que capturam as propriedades estruturais e, por vezes, semânticas do grafo.
- Eles são frequentemente utilizados como uma etapa de pré-processamento para gerar incorporações de nós, que podem então ser usadas como características de entrada para GNNs, especialmente em casos em que as características brutas dos nós não são informativas ou disponíveis.
Assim como na PNL (Processamento Natural de Linguagem), em grafos também temos um conjunto separado de algoritmos para a vetorização de um nó, o que é crucial à medida que avançamos. Alguns dos algoritmos notáveis que discutirei em postagens futuras são:
- DeepWalk: utiliza caminhadas aleatórias para amostrar sequências de nós no grafo e depois emprega técnicas de modelagem de linguagem (como Word2Vec) para aprender incorporações de nós.
- Node2Vec: estende o DeepWalk introduzindo um viés flexível no procedimento de caminhada aleatória, permitindo equilibrar entre busca em largura e busca em profundidade, capturando assim tanto a homogeneidade quanto a equivalência estrutural.
- LINE (Incorporação de redes de informações em grande escala): projetado para preservar tanto as proximidades de primeira ordem (conexões diretas) quanto as de segunda ordem (similaridades entre vizinhos) em redes de informação em grande escala.
- HOPE (Incorporação preservada de proximidade de alta ordem): concentra-se em preservar proximidades de ordens superiores em um grafo, capturando a similaridade entre nós distantes com base em várias medidas de similaridade.
Com isso, encerramos este guia para iniciantes. Espero que esteja motivado o suficiente para ler minhas próximas postagens sobre GNNs e Aprendizado de Grafos.
Artigo escrito por Mehul Gupta. Traduzido por Marcelo Panegali.

