Empréstimos Relâmpago, The Graph e Arbitragem Triangular: Identificando Oportunidades como Tony Soprano, Parte I

Se você deseja lucrar como Tony Soprano, também precisa identificar oportunidades como ele. Encontrar oportunidades lucrativas nos mercados descentralizados de hoje pode ser uma tarefa desafiadora. Com a quantidade avassaladora de dados nos mercados descentralizados, essa tarefa se tornou ainda mais difícil. No entanto, ao utilizar ferramentas como o The Graph, os traders podem obter uma vantagem crítica na descoberta e exploração de oportunidades de arbitragem triangular - assim como Tony faria. O resultado? Maior lucratividade e sucesso no mercado.

Pré-requisitos:

• Compreensão das estruturas de dados de grafos;
• Conhecimento do modelo CFMM (Constant Function Market Maker), da Uniswap (V2).

O que abordaremos:

• Consultas ao The Graph para dados de subgrafos;
• Um algoritmo para descobrir ciclos simples não direcionados.

Chamadas ao The Graph:

Vamos nos concentrar em três mercados descentralizados: Uniswap V2, Uniswap V3 e Sushiswap. Os subgrafos destas plataformas possuem esquemas semelhantes, o que nos permite flexibilidade na construção de nossas consultas GraphQL.

Ao criar nossas chamadas ao The Graph, utilizaremos os seguintes pontos de extremidade para cada DEX e os inseriremos em uma solicitação POST padrão do Axios:

• Uniswap V3: https://api.thegraph.com/subgraphs/name/uniswap/uniswap-v3
• Uniswap V2: https://api.thegraph.com/subgraphs/name/uniswap/uniswap-v2
• Sushiswap: https://api.thegraph.com/subgraphs/name/sushiswap/exchange

async function axios_call(query) {
 try {
   const url = '--- end point ---';

   const { data } = await axios.post(url, query);

   return data;
 } catch (error) {
   console.error(error);
 }
}

Agora que temos nossas solicitações Axios configuradas, que dados exatamente precisamos de nossos pools de liquidez?

• UUIDs (Identificador Único Universal) dos pools de liquidez;
• Reservas de tokens;
• Preços dos tokens;
• UUIDs dos tokens;
• Pontos decimais dos tokens (importante para chamadas na cadeia posteriormente).

Considerando que uma única DEX pode acomodar simultaneamente milhares de pools de liquidez, o escopo parece ser bem amplo e abrangente. Uma maneira de reduzir isso é perguntando: quando surgem oportunidades de arbitragem?

Oportunidades de arbitragem são quase sempre desencadeadas por um volume de mercado mais alto. Portanto, devemos focar nossa indexação em torno do volume. Felizmente, cada subgrafo com o qual estamos trabalhando oferece alguns parâmetros para usarmos.

Considere os seguintes exemplos de consultas GraphQL e parâmetros disponíveis.

---- GraphQL for uniswap V2 and sushiswap -----
{
 pairHourDatas(first: 1000, orderBy: hourlyTxns, orderDirection: desc, where: {hourStartUnix_gte:${-- unix timestamp --}}){
   pair {
     id
     reserve0
     reserve1
     token0Price
     token1Price
       token0 {
        symbol
        id
        decimals
        derivedETH
       }
       token1 {
        symbol
        id
        decimals
        derivedETH
       }
     }
   }
 }

---- GraphQL for uniswap V3 -----
{
 poolHourDatas(first: 1000, orderBy: txCount, orderDirection: desc, where: {periodStartUnix_gte: ${-- unix timestamp -- }}){
   pool {
     id
     feeTier
     token0Price
     token1Price
     liquidity
     tick
     sqrtPrice
       token0 {
         symbol
         decimals
         id
         derivedETH
       }
       token1 {
         symbol
         decimals
         id
         derivedETH
        }
      }
   }
 }

Os parâmetros indexam os LPs (pools de liquidez) com alto volume em USD e alto volume de transações. Além disso, o parâmetro where nos oferece flexibilidade ao especificar um intervalo de tempo como uma marca temporal Unix (útil se você planeja agendar tarefas).

Ao passar cada uma das consultas GraphQL para sua respectiva solicitação POST da Axios, a resposta retornada é um array de pools de liquidez para cada DEX.

Embora cada subgrafo contenha esquemas semelhantes, existem pequenas diferenças nas convenções de nomenclatura de cada um. Portanto, precisamos preparar nossos dados de subgrafo formatando cada pool de liquidez para ter os mesmos nomes de chave. Depois de formatar cada array, os mesclamos e passamos os dados para nosso algoritmo de mapeamento.

Construindo Nosso Algoritmo

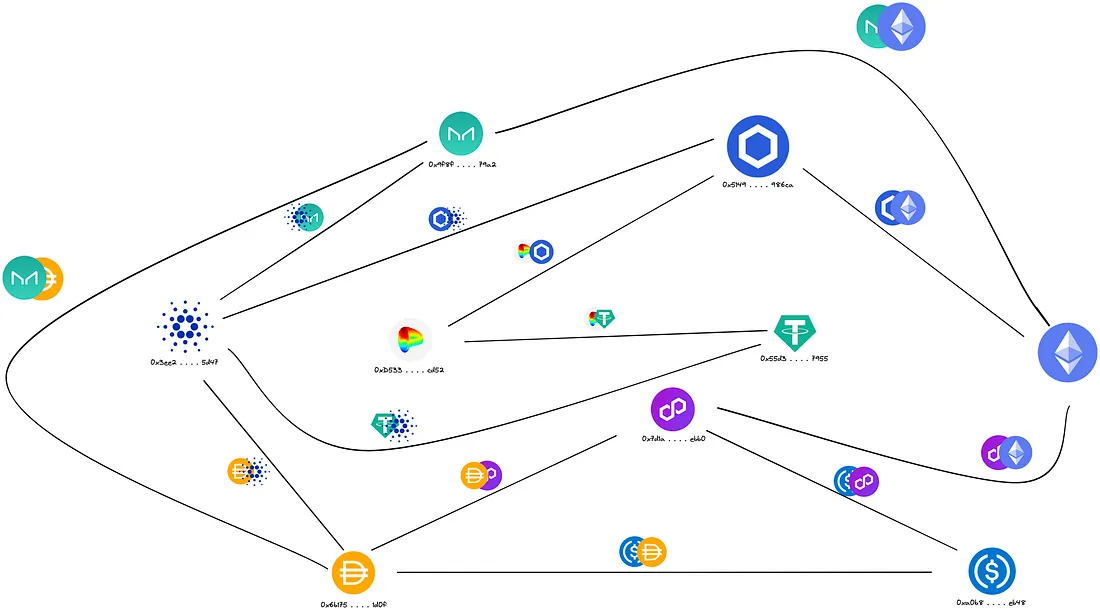
Precisamos pensar em nossos dados coletados como um grafo massivo, onde cada vértice do grafo é um token e suas arestas são pools de liquidez.

O problema está em encontrar o caminho entre cada token, o que pode ser visto como um problema simples de DFS (busca em profundidade). O que precisamos retornar é um subgrafo cíclico não direcionado com três vértices representados como pools de liquidez.

Considerando nossos dados de subgrafo como um problema simples de DFS, podemos dividir nosso algoritmo em algumas etapas:

• Desestruturando os dados do subgrafo;
• Construindo o grafo base e a árvore de expansão;
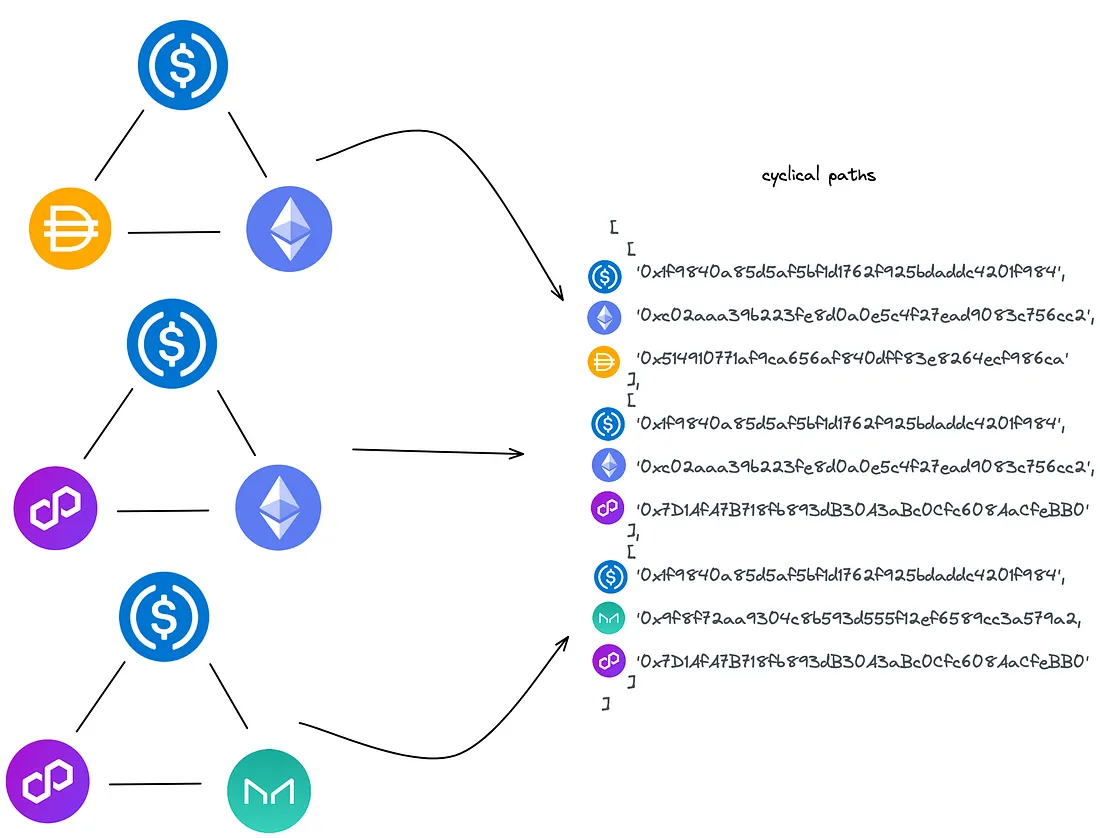
• Encontrando todos os ciclos cíclicos não direcionados com UUIDs de tokens;
• Reconstruindo o ciclo para conter os dados do pool de liquidez;
• Calculando a lucratividade potencial.

Ponto de partida

produce_simple_paths() é a função inicial que recebe os dados do subgrafo e produz uma oportunidade lucrativa de arbitragem triangular.

function produce_simple_exchange_paths(subgraph_data) {

 const path_keys_and_ids = [];

 const [pairUUID, poolAddresses] =
   get_multiple_objects_for_mapping(exchangeObject);
 const { graph, poolAddress } = build_adjacency_list(poolAddresses, pairUUID);
 const tree = get_tree(graph);
 const cycles = get_all_cycles(graph, tree);

 for (const cycle of cycles) {
   const keys = build_base_to_quote_keys(cycle, poolAddress);

   path_keys_and_ids.push({ keys: keys, token_ids: cycle });
 }


 return path_keys_and_ids;
}

I. Desestruturando nossos dados de subgrafo

Usando get_multiple_objects_for_mapping(), produzimos três mapas de hashes (hash maps, ou tabelas de dispersão) distintas ao desestruturar nossos dados de subgrafo.

function get_multiple_objects_for_mapping(
 exchangeObject,
 pairUUID = {},
 poolAddresses = {},
 poolInfo = {}
) {
 for (const pair of exchangeObject) {
   const key1 = `${pair.token0.id}-${pair.token1.id}`;
   const key2 = `${pair.token1.id}-${pair.token0.id}`;

   pairUUID[pair.token0.id]
     ? pairUUID[pair.token0.id].add(pair.token1.id)
     : (pairUUID[pair.token0.id] = new Set([pair.token1.id]));
   pairUUID[pair.token1.id]
     ? pairUUID[pair.token1.id].add(pair.token0.id)
     : (pairUUID[pair.token1.id] = new Set([pair.token0.id]));

   poolAddresses[key1]
     ? poolAddresses[key1].add(`${pair.id}`)
     : (poolAddresses[key1] = new Set([`${pair.id}`]));
   poolAddresses[key2]
     ? poolAddresses[key2].add(`${pair.id}`)
     : (poolAddresses[key2] = new Set([`${pair.id}`]));

   pair.token_ids = [pair.token0.id, pair.token1.id];
   poolInfo[pair.id] = pair;
 }

 return [pairUUID, poolAddresses, poolInfo];
}

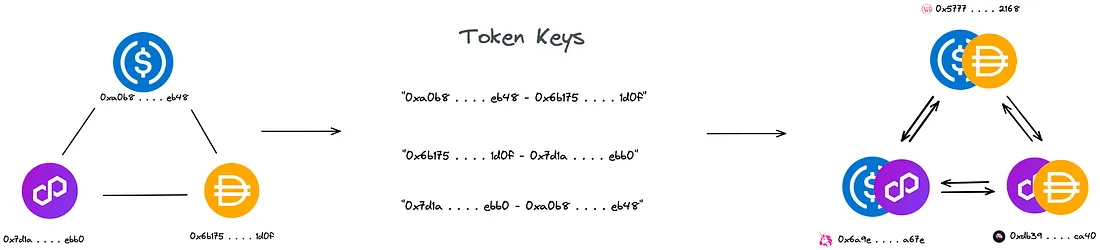
O mapa de hash pairUUID é usado para construir nosso grafo base e a árvore de expansão, a fim de descobrir possíveis ciclos. Em vez de usar o UUID dos pools de liquidez como as arestas, é usado uma chave personalizada para encontrar nosso ciclo. Essa chave consiste em dois UUIDs de tokens separados por um hífen ("-").

Depois de encontrar todos os possíveis ciclos contendo os UUIDs dos tokens, o mapa de hash poolAddress é utilizado para encontrar o UUID do pool de liquidez. Por fim, uma vez que obtemos o UUID do pool de liquidez, ele é usado como chave para obter as informações correspondentes no mapa de hash poolInfo.

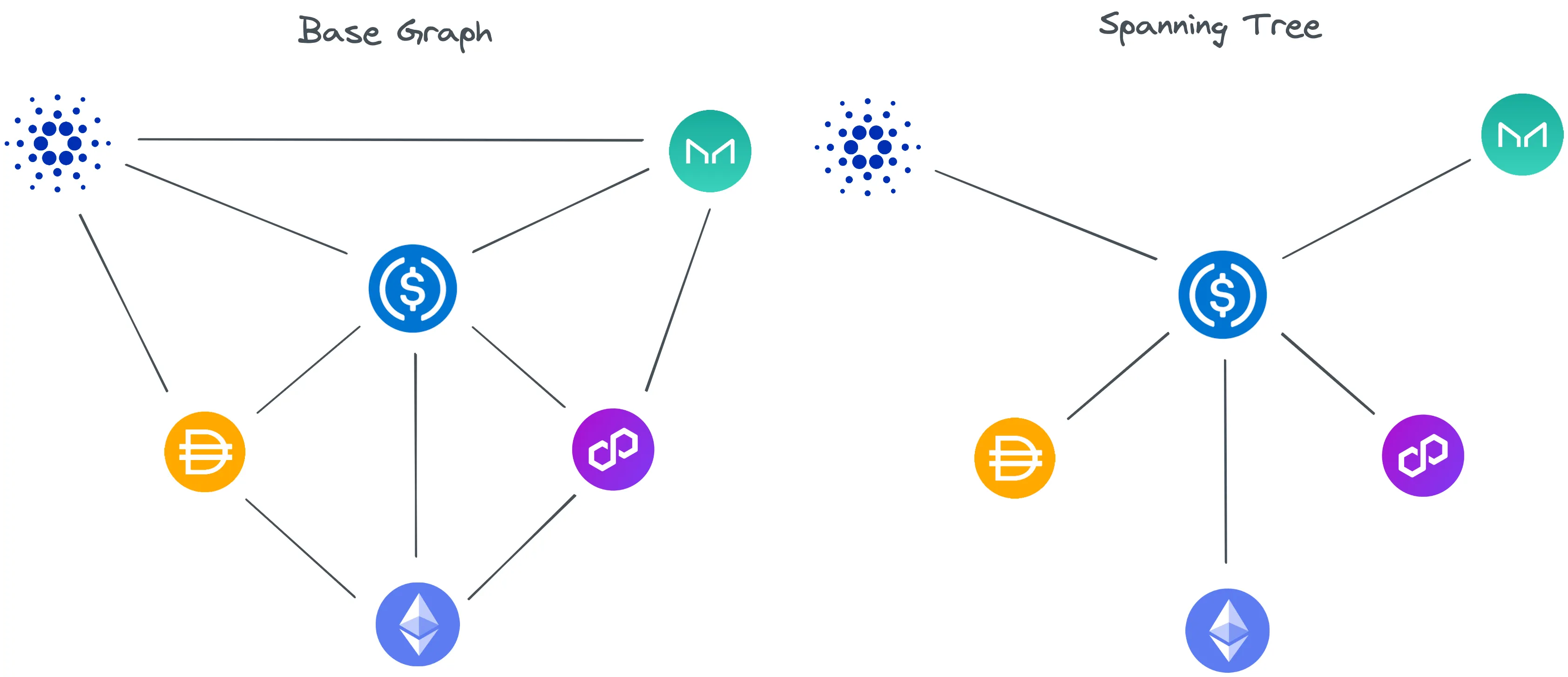
II. Grafo Base e Árvore de Expansão

Os dois grafos são usados para descobrir nossos ciclos. Nosso primeiro grafo representa nosso grafo base. Ele contém todos os UUIDs dos tokens como vértices e todos os seus vizinhos correspondentes.

function build_adjacency_list(poolAddress, pairSymbols) {
 const vertArr = [];

 for (const key in poolAddress) {
   poolAddress[key] = Array.from(poolAddress[key]);
 }

 for (let key in pairSymbols) {
   let verticeObj = {
     vertex: key,
     neighbors: Array.from(pairSymbols[key]),
   };
   vertArr.push(verticeObj);
 }

 let graph = {
   vertices: vertArr,
 };

 return { graph, poolAddress };
}

Nosso segundo grafo representa uma árvore de expansão, que é construída como um mapa de hash. Construímos nossa árvore de expansão iterando sobre nosso grafo base e inserindo os tokens correspondentes. Durante a iteração, um conjunto visitedVertices é mantido e, se um token não for encontrado neste conjunto, ele é adicionado à nossa árvore de expansão.

function get_tree(graph) {
 const spannigTree = new Map();

 for (const coin of graph.vertices) {
   spannigTree.set(coin.vertex, new Set());
 }

 let visitedVertices = new Set();

 graph.vertices.forEach((node) => {
   node.neighbors.forEach((child) => {
     if (!visitedVertices.has(child)) {
       visitedVertices.add(child);
       spannigTree.get(node.vertex).add(child);
       spannigTree.get(child).add(node.vertex);
     }
   });
 });
 return spannigTree;
}

III. Encontrando Nosso Caminho Não Direcionado

Levando em consideração tanto o nosso grafo base quanto a árvore de expansão, os passamos para a função get_all_cycles(), que realiza uma travessia na árvore de expansão. Para encontrar um ciclo, usamos as "arestas removidas" entre os tokens produzidos pela função get_rejected().

function get_all_cycles(graph, spannigTree) {
 let cycles = [];
 let rejectedEdges = get_rejected(graph, spannigTree);

 rejectedEdges.forEach((edge) => {
   const ends = edge.split('-');
   const start = ends[0];
   const end = ends[1];

   const cycle = find_cycle(start, end, spannigTree);

   if (cycle && cycle.length <= 3) {
     cycles.push(cycle);
   }
 });
 return cycles;
}

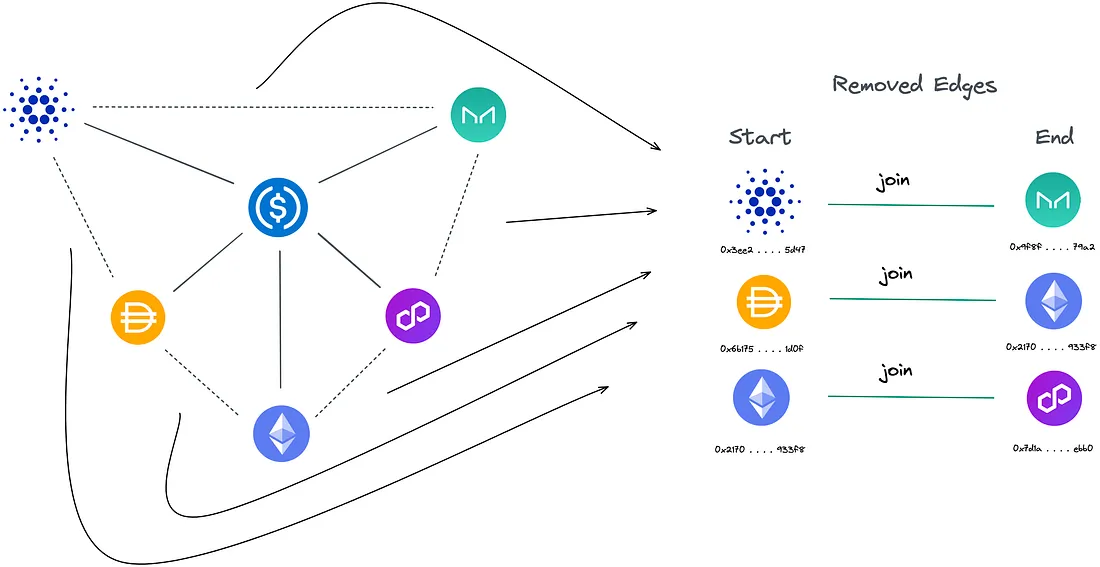
get_rejected() encontra as "arestas removidas" enquanto iteramos pelo nosso grafo base e construímos nossa árvore de expansão. Se um token no conjunto correspondente da árvore de expansão não estiver presente, ele é considerado uma "aresta removida" e, portanto, parte de um possível ciclo.

function get_rejected(graph, tree) {
 let rejectedEdges = new Set();

 graph.vertices.forEach((node) => {
   if (tree.has(node.vertex)) {
     node.neighbors.forEach((child) => {
       if (!tree.get(node.vertex).has(child)) {
         if (!rejectedEdges.has(child + '-' + node.vertex)) {
           rejectedEdges.add(node.vertex + '-' + child);
         }
       }
     });
   }
 });
 return rejectedEdges;
}

Um ciclo pode ser encontrado no grafo base que conecta as duas extremidades da aresta removida. Como a árvore de expansão não contém ciclos, é possível traçar um caminho de qualquer token para outro. Ao traçar o ciclo entre as duas extremidades da aresta removida dentro da árvore de expansão, um caminho pode ser obtido.

Utilizando a aresta removida, a dividimos e passamos o token inicial e o token final para a função find_cycle(). Essa função realiza recursivamente uma travessia DFS na nossa árvore de expansão.

A recursão termina quando o vértice final é alcançado ou quando todos os vértices são visitados. Uma vez que o vértice final é alcançado, o caminho percorrido até alcançá-lo é considerado um ciclo.

function find_cycle(
 start_token,
 end_token,
 spannigTree,
 visited = new Set(),
 parents = new Map(),
 current_node = start_token,
 parent_node = ' '
) {
 let cycle = null;
 visited.add(current_node);
 parents.set(current_node, parent_node);
 const destinations = spannigTree.get(current_node);
 for (const destination of destinations) {
   if (destination === end_token) {
     cycle = get_cycle_path(start_token, end_token, current_node, parents);
     return cycle;
   }
   if (destination === parents.get(current_node)) {
     continue;
   }
   if (!visited.has(destination)) {
     cycle = find_cycle(
       start_token,
       end_token,
       spannigTree,
       visited,
       parents,
       destination,
       current_node
     );
     if (cycle) {
       return cycle;
     }
   }
 }

 return cycle;
}

Por fim, quando um caminho é descoberto, a função get_cycle_path() é invocada. Ela retrocede na árvore de expansão do final para o início e valida o ciclo. O resultado retornado é um array aninhado de UUIDs de tokens.

function get_cycle_path(start, end, current, parents) {
 let cycle = [end];
 while (current !== start) {
   cycle.push(current);
   current = parents.get(current);
 }
 cycle.push(start);
 return cycle;
}

IV. Reconstruindo Nossos Ciclos

A reconstrução dos nossos ciclos é composta por duas etapas. Primeiro, obtemos os UUIDs dos pools de liquidez dos caminhos. Em seguida, obtemos as informações dos pools de liquidez. Utilizando os dois mapas de hashes construídos durante a desestruturação, esse processo é simplificado.

Para encontrar os UUIDs dos pools de liquidez, iteramos sobre nosso array de caminhos de tokens e chamamos a função build_base_to_quote_keys().

function build_base_to_quote_keys(cycle, poolAddress) {
 const [first_token_id, second_token_id, third_token_id] = cycle;
 const first_pool_key = `${first_token_id}-${second_token_id}`;
 const second_pool_key = `${second_token_id}-${third_token_id}`;
 const third_pool_key = `${third_token_id}-${first_token_id}`;

 const addresses = [
   poolAddress[first_pool_key],
   poolAddress[second_pool_key],
   poolAddress[third_pool_key],
 ];

 const all_paths_from_cycle = get_all_address_permutations(addresses);

 return all_paths_from_cycle;
}

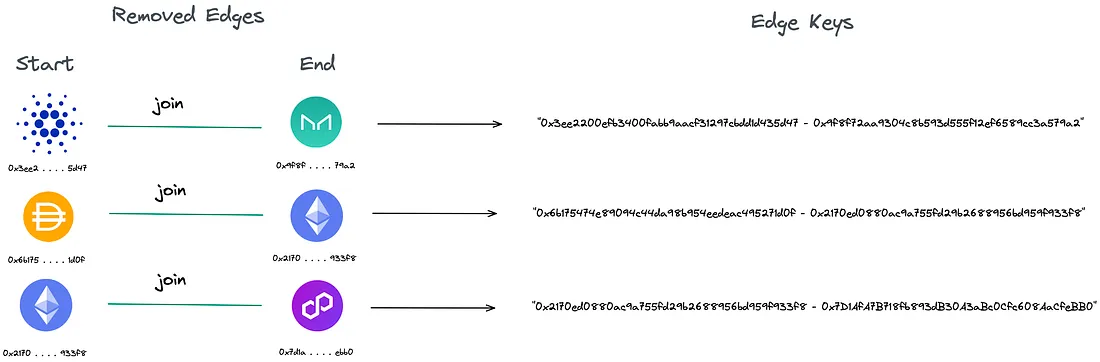
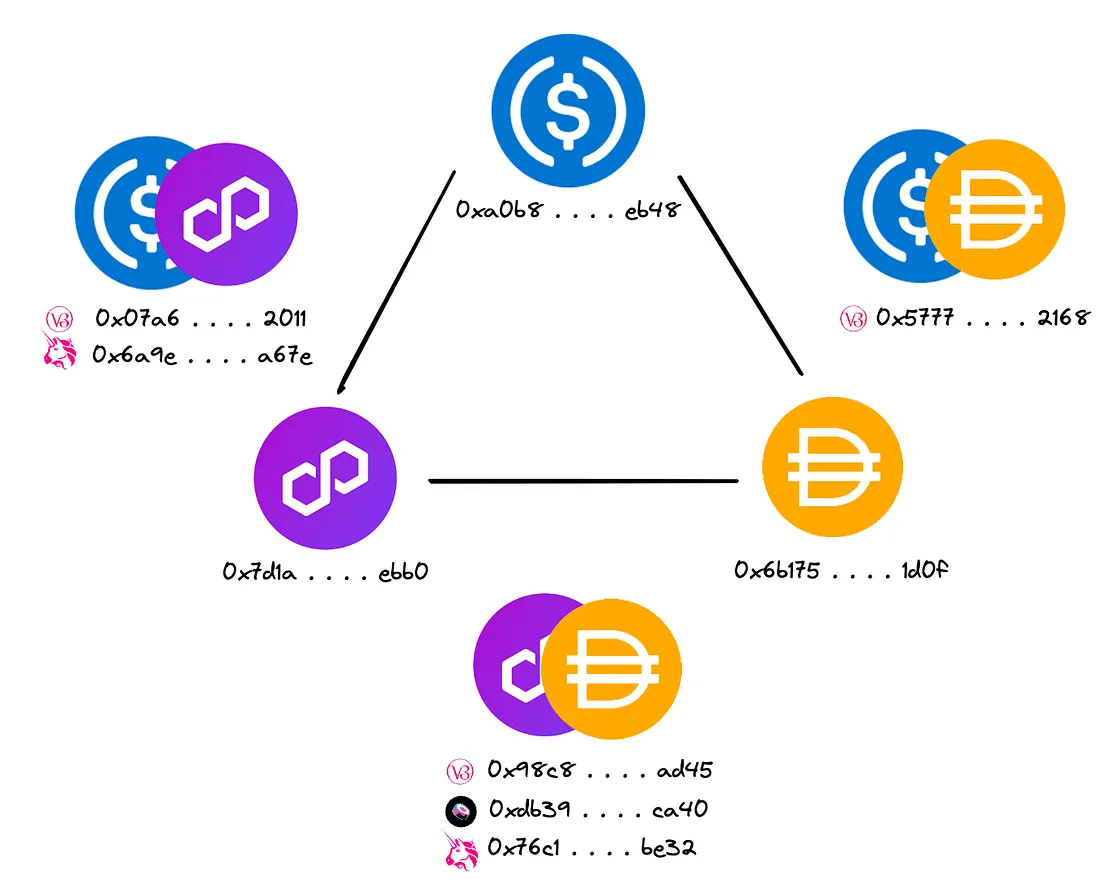
Cada token possui um complemento (de acordo com sua posição indexada) que é reunido novamente para construir uma chave de token. Pegamos cada chave de token e a passamos para o mapa de hash poolAddress, que busca o UUID do nosso pool de liquidez. Pode haver ocasiões em que nossas chaves de token recuperam vários UUIDs. Em outras palavras, outras exchanges possuem as mesmas combinações de tokens.

Com base no exposto acima, a função get_all_address_permutations() recebe o array de UUIDs dos pools de liquidez e retorna todas as suas permutações.

function get_all_address_permutations(
 addresses,
 loop = 0,
 result = [],
 current = []
) {
 if (loop === addresses.length) {
   result.push(current);
 } else {
   addresses[loop].forEach((item) => {
     get_all_address_permutations(addresses, loop + 1, result, [
       ...current,
       item,
     ]);
   });
 }

 return result;
}

Cada permutação produzida é considerada um ciclo com o mesmo caminho de tokens, mas com um pool de liquidez diferente para negociar. Após o processo ser concluído, teremos uma lista de elementos que contêm o caminho inicial de UUIDs de tokens e um array de UUIDs de pools de liquidez representando caminhos de negociação únicos.

Qual é o próximo passo?

Na parte 2, exploraremos os métodos e ferramentas necessários para determinar a lucratividade das oportunidades de arbitragem triangular descobertas nos mercados descentralizados. Os traders podem aproveitar esse conhecimento para aproveitar essas oportunidades e aumentar suas chances de sucesso.

Vamos nos aprofundar em como fazemos chamadas de dados na cadeia para avaliar cada caminho em potencial descoberto. Confira a parte 2 para obter insights valiosos que podem ajudar a aprimorar suas estratégias de negociação e alcançar maior lucratividade no mercado: Empréstimos Relâmpago, The Graph e Arbitragem Triangular: Identifique Oportunidades como Tony Soprano Pt II.

Repositório do GitHub.

Fontes e leituras adicionais

• Encontrando ciclos simples com mais profundidade
• The Graph - nosso Protocolo de Indexação de Blockchain
• Livro de Desenvolvimento da Uniswap V3

Artigo original publicado por Brennan Skinner. Traduzido por Paulinho Giovannini.