No mundo das criptomoedas, a negociação e os gastos funcionam apenas se as transações não puderem ser gastas duas vezes. Assim, duas verificações são realizadas: A primeira, uma transação deve ser válida; a segunda, uma transação não deve ter sido gasta. Essencialmente, a primeira verificação é um teste de pertinência de um conjunto e a segunda é um teste de não pertinência de um conjunto. Um teste de pertinência é usado para determinar se um elemento está presente em um conjunto de valores. Um teste de não pertinência é usado para determinar a ausência de um elemento em um conjunto de valores. O conjunto de valores mais popular em produção é a Árvore de Merkle, pois verificar se um valor está no conjunto não requer conhecimento de toda a árvore, apenas o suficiente do subconjunto para validar um caminho específico para um valor. No entanto, aplicar provas de conhecimento zero (ZKPs) a uma Árvore de Merkle é complicado. As ZKPs são utilizadas para ocultar o valor e o caminho que está sendo verificado para preservar a privacidade. Mas, para isso, ZKPs personalizadas baseadas em circuitos devem ser projetadas considerando os vários parâmetros de configuração:
- Qual função de hash criptográfica usar?
- Qual a profundidade máxima?
- As transações podem ser podadas?
- Seleção de curvas elípticas;
- Tempo de prova e requisitos computacionais;
- Hora de verificação;
- Tamanho da prova;
- Comprovação do tamanho da chave;
- Definir tamanho.
zkSNARK é a técnica que recebe mais atenção e pesquisa para a otimização do panorama geral. A Coda está aplicando o zkSNARKS de maneira recursiva para reduzir o tamanho da blockchain para validação. A ZCash usa o SNARKS para anonimizar as partes e ocultar os valores negociados realizando várias provas: uma para validação de assinatura, a outra para garantir que a transação seja válida. No entanto, SNARKs vêm com algumas desvantagens. Por um lado, o circuito aritmético desejado precisa ser projetado para que uma string de referência comum (CRS) adequada possa ser gerada. A CRS é o parâmetro público do sistema ZCash. Então, qual sistema o SNARK deve usar? Spartan, Halo, Hyrax, Libra, Sonic, Plonk, Marlin... Cada sistema tem suas compensações entre configurações confiáveis, tamanho de prova, pares bilineares ou outras curvas elípticas, geração de prova e tempo de geração. Os SNARKS não são os únicos sistemas baseados em circuitos que podem ser usados. Bulletproofs, Bulletproofs+, STARKS, SNARGS… a lista continua, mas não há um vencedor claro e todos eles exigem conhecimentos avançados em criptografia. Felizmente, existe outra primitiva criptográfica para realizar determinadas provas rápidas de pertinência (e não pertinência) que preserva a privacidade (na medida em que o elemento que está sendo verificado não é revelado) e fornece provas sucintas. Estes são chamados de acumuladores criptográficos.
Acumuladores criptográficos
Os acumuladores permitem que as partes provem que um elemento x está em um conjunto S ou não, independentemente do número de elementos em S, sem revelar qual elemento foi verificado. Os acumuladores funcionam adicionando um valor x a (ou removendo) um acumulador A de tamanho constante e provando que a testemunha de pertinência u, quando combinada com x, é igual ao acumulador A. Os valores do acumulador são resumos curtos de comprimento fixo (semelhantes às funções de hash), mas também suporta provas curtas para verificações de pertinência e não pertinência para qualquer elemento no conjunto. Em outras palavras, um acumulador representa todo o conjunto de elementos por um único valor, o tamanho é independente do número de elementos. Um acumulador é dinâmico se os elementos podem ser adicionados ou removidos de forma eficiente do conjunto. Caso contrário, o acumulador é estático. Um acumulador universal é dinâmico e suporta provas de pertinência e não pertinência. Caso contrário, diz-se que o acumulador suporta apenas provas de pertinência.
Devido à configuração mais simples e provas mais curtas, estes oferecem uma alternativa interessante aos SNARKs. Este não é um conceito novo para substituir a parte de teste de pertinência de provas por um acumulador [ver OWWB19]. No entanto, o OWWB19 propõe o uso de um acumulador dentro do SNARK em vez de descartar completamente os SNARKs. Eles mostram que a combinação do acumulador SNARK tem requisitos de custo mais baixos em espaço e desempenho, como também será mostrado neste artigo.
Os acumuladores se enquadram nas três categorias a seguir: os de Ordem Desconhecida, por exemplo. [Sander97, BP97, BM93, CL02, LLX07, Lip12, BCDLRSY17, BBF18, OWWB19, DGS20], os Mapas Bilineares [Nguyen05, ATSM09, CKS08, DT08, Thakur19, VB20] e os baseados em hash [CHKO08]. Cada um oferece compensações entre parâmetros de configuração, tamanhos de acumulador, desempenho de testemunha e prova e espaço. Os acumuladores de ordens desconhecidas são subdivididos em baseados em RSA e baseados em curvas hiperelípticas (ordens de classe). O restante deste artigo se concentra na história sobre a implementação do acumulador baseado em RSA e como eles funcionam.
Os acumuladores RSA oferecem a compensação mais eficiente entre o número de parâmetros de configuração, atualização de requisitos de testemunha, cálculo de prova e concisão. O valor do acumulador e a testemunha são do tamanho de um módulo RSA. Quando implementado, o módulo, o valor do acumulador e as testemunhas são de 256 bytes com elementos de 32 bytes, e as provas de pertinência são de 800 bytes e requerem apenas 90 milissegundos (ms) para calcular, usa 2 KB de RAM e 30 ms para verificar. As atualizações de testemunhas podem ser calculadas em 5 a 10 ms, dependendo do sistema subjacente. As provas de não pertinência exigem a criação de duas provas, mas as provas podem ser calculadas em paralelo, o que leva o mesmo tempo, mas o dobro do espaço com 1,6 KB.
Compare isso com o SNARK JubJub do ZCash, que requer o download de toda a Árvore de Merkle, que tem alguns gigabytes, baixando a chave de prova em torno de 32 MB, gerando uma testemunha de 458 KB em 1 segundo usando 150 MB de ram, gerando a prova usando 106 MB de RAM, levando 3 segundos e produzindo uma prova de byte de 1,4 KB [ CryptQuest2018]. A vantagem dos acumuladores criptográficos é que as provas são sucintas e rápidas de computar.
Como funciona
Para configurar um acumulador RSA, é necessário gerar dois primos seguros (p, q) de tamanho suficiente (≥ 1024 bits) para calcular o módulo coprimo n e criar um gerador que seja um resíduo quadrático g, essencialmente encontrando um número aleatório e calculando a esquadria modular. g é o valor do acumulador vazio, usado para criar provas de não pertinência. A geração de ( p, q) geralmente é feita com um revendedor confiável, mas alguns métodos distribuídos permitem que isso seja feito de maneira descentralizada [ AVD19] (sem necessidade mínima de confiança), embora mais complicado. Cada elemento a ser acumulado deve ser um número primo único. Os valores podem ser mapeados para números primos por uma função que geralmente é uma tabela de pesquisa ou um algoritmo de hash e adicionados ao conjunto S. O valor do acumulador é calculado da seguinte forma:
Os valores são acumulados calculando a exponenciação modular do valor do acumulador atual para o novo elemento. As remoções podem ser calculadas de duas maneiras: com e sem o conhecimento de p, q. O criador do acumulador confiável (ou revendedor) usa p, q para calcular o totiente de Euler e calcular:
Lembre-se de seus p's e q's, porque sem eles, o acumulador precisa ser recalculado multiplicando novamente todos os elementos no acumulador com uma exponenciação modular. Um usuário tem uma testemunha de pertinência ou testemunha de não pertinência (ou ambas), dependendo do tipo da prova esperada por uma terceira parte confiável. A testemunha de adesão u é computada:
A testemunha deve ser atualizada para refletir quaisquer alterações feitas no acumulador, caso contrário, as provas serão inválidas. Os usuários podem atualizar com eficiência suas testemunhas à medida que os elementos são adicionados e excluídos do acumulador. Infelizmente, implementar a variante de não pertinência foi muito mais complicado do que a versão de pertinência. O artigo científico sobre técnicas de loteamento (batching) mostra a testemunha de não pertinência como:
Isso funciona bem. As provas computam normalmente e tudo funciona muito bem. A ressalva acontece ao tentar atualizar a testemunha w. O artigo sobre loteamento se refere a outro artigo científico, LLX07, para esta matemática. A princípio, a matemática parece simples na seção 4.2, onde diz para fazer o seguinte para uma adição:
Para verificar a correção da atualização, calcule uma testemunha de não pertinência atual sem fazer uma atualização e compare a igualdade. No final, eles não se correspondem (virando a mesa).
A Dor de Cabeça da Implementação
Para verificar se a correspondência está funcionando corretamente, insiro várias declarações assert que verificam as suposições feitas no LLX07. Todos passam menos a suposição final. Depois de ficar intrigado com isso por um tempo, li o LLX07 desde o início e descobri que a testemunha de não pertinência difere por um sinal, Bg-b. Fiz essa alteração e as atualizações de não pertinência funcionaram corretamente, mas agora as provas estão quebradas. A única opção é trabalhar com a matemática novamente para ter certeza de que as coisas estão corretas e procurar onde não estão. A equação em falta aqui é a prova que computa a prova de conhecimento de expoentes (POE, prova de que os expoentes são conhecidos pelo provador sem revelá-los) com o acumulador atual A e valor de não pertinência a. Ao invés de inverter V, o gerador g precisou ser invertido, movendo a operação inversa modular. Aqui está um antes e depois:
Envie V, Q, B para serem verificados:
Por que essa mudança? Vejamos o antes e depois em profundidade.
Antes:
B foi alterado para B=gb e depois para B=g-b, e a antiga equação se torna:
O objetivo da prova de não pertinência é fazer com que os expoentes sejam iguais ax*+bx = 1. Assim, a mudança para g-¹. Com essa alteração fica:
Muitas vezes, uma das partes mais complicadas da implementação da criptografia é verificar se há erros nas equações e fazer as correções necessárias. O contato para o artigo sobre loteamento foi notificado dessas alterações, mas ainda não respondeu à atualização. A implementação do código funcional pode ser encontrada aqui. Vemos que o código, embora tivesse alguns problemas, era muito mais fácil de usar e implementar do que o SNARKs.
Fique atento ao blog da Coinbase Engineering, pois um artigo de acompanhamento abordará os Acumuladores Bilineares para comparar e contrastar RSA e SNARKs.
Se você estiver interessado na complexidade da aplicação da criptografia de conhecimento zero, a Coinbase está contratando.
Artigo publicado no site do CryptoHopper, originalmente escrito pela Coinbase. Tradução por Paulinho Giovannini.


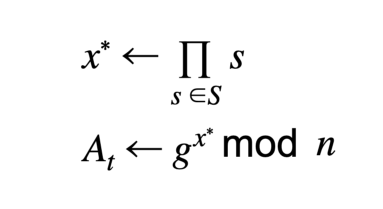
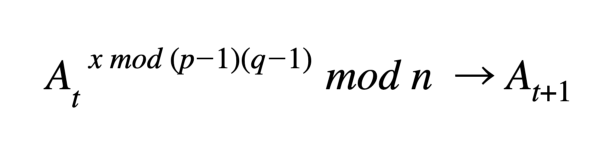
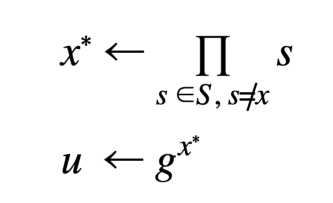
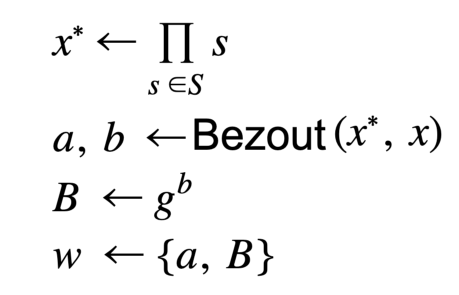



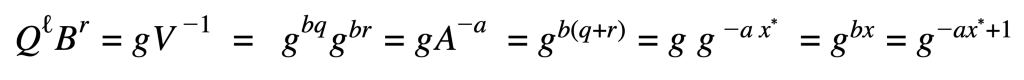
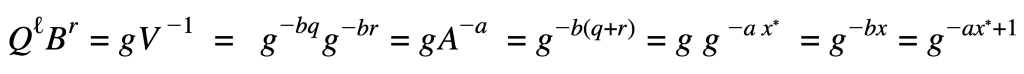
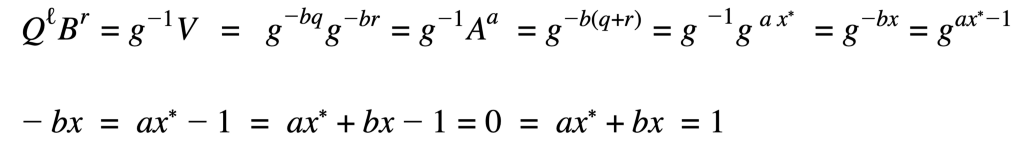







Latest comments (0)