O artigo sobre ativos confidenciais apresentado por Andrew Poelstra, Adam Back, Mark Friedenbach, Gregory Maxwell e Pieter Wuille descreve a implementação de ativos confidenciais no Bitcoin. Publicado em 2016, o artigo apresenta o conceito de valores confidenciais, que permite que os usuários ocultem os valores das transações e, ao mesmo tempo, preservem a integridade do blockchain. Ele usa as provas de Pedersen Commitment e Back-Maxwell range para ocultar os valores e a chave pública do proprietário em um ponto de curva elíptica. Usando essa abordagem, podemos deixar de armazenar valores públicos no UTXO e colocar o ponto elíptico em seu lugar.
O objetivo deste artigo é explicar a implementação da solução descrita em termos de sistema compatível com EVM - usando contratos inteligentes Solidity. Também será fornecida uma implementação em Golang.
Vamos começar pela teoria
Pedersen commitment é um ponto elíptico construído como C = aH + rG, em que a pode ser um valor e r será uma chave privada do proprietário. Não há como revelar a ou r até que alguém os forneça como estão.
Basicamente, os ativos confidenciais funcionam da seguinte maneira: imagine que temos uma Alice que deseja enviar 5 ETH para Bob. Alice possui um UTXO que armazena o compromisso de 5 ETH C1. Em seguida, Bob, como receptor, cria o compromisso C2 para os 5 ETH que ele deseja receber. Depois, eles estão construindo uma transação que gasta C1 na saída C2. Na cadeia, temos que verificar se os valores de entrada e saída resultantes são iguais e se ninguém tenta enganar nosso sistema cunhando tokens do ar. Como um ponto da curva elíptica suporta uma operação de adição, precisamos adicionar o C1 e o ponto inverso С2' (vamos definir essa operação como "-"). Portanto, C = C1 - C2 = 5H + rAliceG - 5H - rBobG = (rAlice - rBob) * G. Então, para verificar a exatidão das entradas e saídas fornecidas, precisamos fornecer a assinatura da chave pública (rAlice - rBob) * G. Se os valores não forem iguais, não haverá como fornecer essa assinatura. Portanto, a exatidão da assinatura significa que Alice e Bob conhecem suas chaves privadas de compromissos e também que os valores de entrada menos saída são iguais a zero. A maneira mais adequada de fornecer uma assinatura descrita é usar assinaturas Schnoor agregadas, em que Bob e Alice podem construir assinaturas por si mesmos e, em seguida, agregá-las para obter uma assinatura agregada para a chave pública (rAlice - rBob) * G.
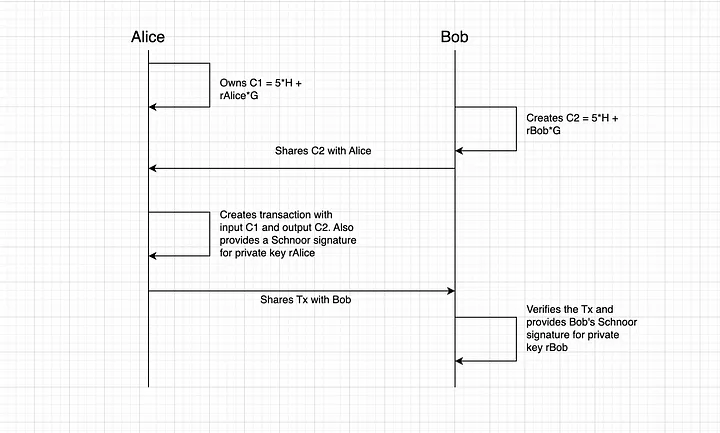
Em resumo, vamos explicar como funciona a assinatura Schnoor:
PubKey = rG
----
Signing
k = rand()
R = kG
s = k - Hash(msg|P)*r
Sig = <s, R>
----
Verification
Check that sG = R - Hash(msg|P)*P
----
Aggregation
PubAggr = PubAlice + PubBob
SigAlice = <kAlice - Hash(msg|PubAggr)*rAlice, RAlice>
SigBob = <kBob - Hash(msg|PubAggr)*rBob, RBob>
SigAggr = SigAlice + SigBob = < kAlice+kBob - Hash(msg|PubAggr)*(rAlice+rBob), RAlice+RBob >
Observe que é necessário o conhecimento da chave pública agregada por ambos os lados.
A última coisa que precisa ser discutida antes da implementação são as provas de alcance. Os sistemas de blockchain (Ethereum, por exemplo) usam uint256 para armazenar valores. Portanto, estamos trabalhando no campo 2^n (n = 256) e, além disso, estamos trabalhando em um campo de curva elíptica selecionado (menor que 2²⁵⁶) que pode ser transbordado por operações de adição e subtração.
Como exemplo, vamos usar o campo com ordem 10. Se tivermos um valor de entrada 6 e valores de saída em dois compromissos 9 e 7, o resultado da subtração será zero [6-9-7=0 (mod 10)]. Portanto, teremos 10 tokens cunhados do ar. Para evitar isso, temos que reduzir a ordem de campo dos valores — fornecendo o conhecimento zero de que o valor armazenado está em [0; 2^k) onde k < n.
O artigo sobre ativos confidenciais descreve a prova de intervalo de Back-Maxwell que fornece uma prova de conhecimento zero com tamanho O(k). Também existe uma prova mais eficiente, a Bulletproof, que cria uma prova com tamanho O(log k).

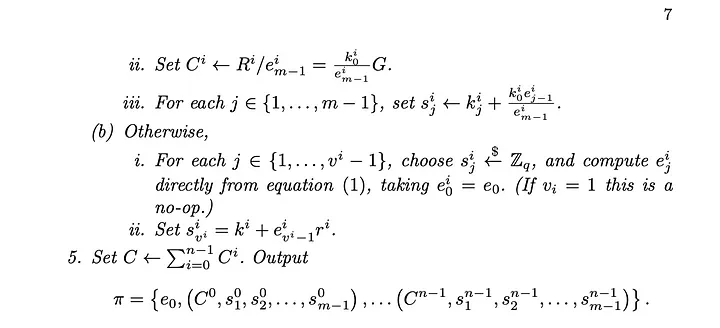
A prova de intervalo de Back-Maxwel (Back-Maxwell rangeproof)l descrita a partir do artigo de ativos confidenciais funciona para qualquer sistema numérico posicional com qualquer base e pode ser simplesmente modificado para uso com a base 2.
Implementação em Golang
Você pode explorar a implementação em Golang do Back-Maxwell rangeproof lá. Aqui está o exemplo de uso (de pedersen_test.go):
func TestPedersenCommitment(t *testing.T) {
proof, commitment, prv, err := CreatePedersenCommitment(10, 5)
if err != nil {
panic(err)
}
reconstructedCommitment := PedersenCommitment(big.NewInt(10), prv)
fmt.Println("Constructed commitment with prv key: " + reconstructedCommitment.String())
fmt.Println("Response commitment: " + commitment.String())
fmt.Println("Private Key: " + hexutil.Encode(prv.Bytes()))
if err = VerifyPedersenCommitment(commitment, proof); err != nil {
panic(err)
}
}
Observe que o Back-Maxwell rangeproof cria o compromisso para qualquer valor dado que esteja em um intervalo definido e, como resultado, fornece o compromisso e a chave privada para esse compromisso.
Curva elíptica
Antes de implementar o sistema desejado no Solidity, precisamos escolher a curva elíptica com a qual trabalhar. A solução óbvia é usar a curva secp256k1 nativa da Ethereum, mas, infelizmente, o Solidity não oferece uma maneira rápida de realizar cálculos elípticos nela. Implementar a adição e a multiplicação por nós mesmos leva ao problema do gas fora do alcance - essas operações custam muito caro. Portanto, precisamos usar contratos de curva elíptica já pré-compilados do EIP-196 - alt_bn128.
Vamos criar uma biblioteca simples para o uso do alt_bn128:
// SPDX-License-Identifier: MIT
pragma solidity >=0.6.0;
/**
* Referenciado em https://github.com/kendricktan/heiswap-dapp/blob/master/contracts/AltBn128.sol
*/
library EllipticCurve {
/// @note o ECPoint armazena as coordenadas do ponto da curva elíptica.
struct ECPoint {
uint256 _x;
uint256 _y;
}
/// @note Ponto H base do compromisso de Pedersen
uint256 public constant Hx =
0x2cb8b246dbf3d5b5d3e9f75f997cd690d205ef2372292508c806d764ee58f4db;
uint256 public constant Hy =
0x1fd7b632da9c73178503346d9ebbb60cc31104b5b8ce33782eaaecaca35c96ba;
/// @note Ponto de base G do compromisso de Pedersen
uint256 public constant Gx =
0x2f21e4931451bb6bd8032d52b90a81859fd1abba929df94621a716ebbe3456fd;
uint256 public constant Gy =
0x171c62d5d61cc08d176f2ea3fe42314a89b0196ea6c68ed1d9a4c426d47c3232;
/// @note Número de elementos no campo (geralmente chamado de `q`)
/// n = n(u) = 36u^4 + 36u^3 + 18u^2 + 6u + 1
uint256 public constant N =
0x30644e72e131a029b85045b68181585d2833e84879b9709143e1f593f0000001;
/// @notice p = p(u) = 36u^4 + 36u^3 + 24u^2 + 6u + 1
/// Pedido de campo
uint256 public constant P =
0x30644e72e131a029b85045b68181585d97816a916871ca8d3c208c16d87cfd47;
/// @notice (p+1) / 4
uint256 public constant A =
0xc19139cb84c680a6e14116da060561765e05aa45a1c72a34f082305b61f3f52;
function ecAdd(
ECPoint memory _p1,
ECPoint memory _p2
) public view returns (ECPoint memory) {
uint256[4] memory _i = [_p1._x, _p1._y, _p2._x, _p2._y];
uint256[2] memory _r;
assembly {
// chama ecadd precompile
// As entradas são: x1, y1, x2, y2
if iszero(staticcall(not(0), 0x06, _i, 0x80, _r, 0x40)) {
revert(0, 0)
}
}
return ECPoint(_r[0], _r[1]);
}
function ecMul(
ECPoint memory _p,
uint256 s
) public view returns (ECPoint memory) {
// Com uma chave pública (x, y), isso calcula p = escalar * (x, y).
uint256[3] memory _i = [_p._x, _p._y, s];
uint256[2] memory _r;
assembly {
// chama ecmul precompile
// As entradas são: x, y, escalar
if iszero(staticcall(sub(gas(), 2000), 0x07, _i, 0x60, _r, 0x40)) {
revert(0, 0)
}
}
return ECPoint(_r[0], _r[1]);
}
function ecBaseMul(uint256 s) public view returns (ECPoint memory) {
// Com uma chave pública (x, y), isso calcula p = escalar * (x, y).
uint256[3] memory _i = [Gx, Gy, s];
uint256[2] memory _r;
assembly {
// chama ecmul precompile
// as entradas são: x, y, scalar
if iszero(staticcall(sub(gas(), 2000), 0x07, _i, 0x60, _r, 0x40)) {
revert(0, 0)
}
}
return ECPoint(_r[0], _r[1]);
}
function ecSub(
ECPoint memory _p1,
ECPoint memory _p2
) internal view returns (ECPoint memory) {
_p2 = ecNeg(_p2);
return ecAdd(_p1, _p2);
}
function ecNeg(ECPoint memory _p) internal pure returns (ECPoint memory) {
if (_p._x == 0 && _p._y == 0) return _p;
return ECPoint(_p._x, P - (_p._y % P));
}
function onCurve(ECPoint memory _p) public pure returns (bool) {
uint256 beta = mulmod(_p._x, _p._x, P);
beta = mulmod(beta, _p._x, P);
beta = addmod(beta, 3, P);
return beta == mulmod(_p._y, _p._y, P);
}
}
Ele usa as chamadas estáticas para 0x06 e 0x07 para adição de pontos e multiplicação escalar. Observe também que é recomendável que os pontos H e G sejam construídos por uma configuração confiável, de modo que ninguém, por si só, possa revelar a parte escalar.
Definições de implementação
Como os ativos confidenciais funcionam com base no modelo UTXO, precisamos de um contrato inteligente UTXO que emulará os UTXOs em termos do sistema EVM. Vamos definir a seguinte interface (como exemplo, trabalharemos com o ativo nativo EVM, mas ela pode ser estendida para ser usada com qualquer ativo possível):
// SPDX-License-Identifier: MIT
pragma solidity ^0.8.0;
import "../EllipticCurve.sol";
/**
* @title UTXO-ETH interface
*/
interface IUTXO {
/// @note UTXO é uma estrutura de base que armazena o compromisso de Pedersen com o valor e o sinalizador _valuable.
struct UTXO {
EllipticCurve.ECPoint _c;
bool _valuable;
}
/// @note A prova contém os dados para verificar a prova de intervalo de Back-Maxwell para o compromisso de Pedersen.
struct Proof {
uint256 _e0;
EllipticCurve.ECPoint[] _c;
uint256[] _s;
}
/// @note a testemunha contém a assinatura Schnorr agregada para a operação de transferência.
struct Witness {
EllipticCurve.ECPoint _r;
uint256 _s;
}
/// @notice Inicialização do novo UTXO (sem depósito). Use para criar a saída de transferência.
/// Nenhuma informação sobre o valor é necessária. A prova de intervalo de Back-Maxwell deve ser válida.
/// @param _commitment Ponto de compromisso de Pedersen.
/// @param _proof Prova de intervalo de Back-Maxwell..
function initialize(
EllipticCurve.ECPoint memory _commitment,
Proof memory _proof
) external returns (uint256);
/// @notice Deposite ETH e crie o UTXO correspondente.
/// @param _publicKey Chave pública: `prv * G`.
/// @param _witness Assinatura Schnorr para a chave pública fornecida.
function deposit(
EllipticCurve.ECPoint memory _publicKey,
Witness memory _witness
) external payable returns (uint256);
/// @notice Retirar UTXO.
/// @param _id Índice da UTXO.
/// @param _to Endereço do destinatário
/// @param _amount quantia em wei a ser retirada.
/// @param _witness Assinatura Schnorr para a chave pública do UTXO.
@notice A testemunha contém a assinatura Schnorr agregada para a operação de transferência.
function withdraw(
uint256 _id,
address payable _to,
uint256 _amount,
Witness memory _witness
) external;
/// @notice Transferir ETH (anônimo)
/// @param _inputs Índice UTXO de entrada.
/// @param _outputs Índice UTXO de saída.
/// @param _witness Assinatura Schnorr para chave pública agregada (saída - entrada).
function transfer(
uint256[] memory _inputs,
uint256[] memory _outputs,
Witness memory _witness
) external;
}
A estrutura UTXO representa um UTXO simples que armazena um ponto elíptico e um campo valioso, que define se nosso UTXO contém algum valor ou se ele foi gasto ou ainda não foi ativado.
A estrutura Proof representa o rangeproof de Back-Maxwell para o valor comprometido. Ela será usada apenas uma vez, durante a criação do compromisso.
A estrutura Witness representa a assinatura Schnoor que será usada na operação de transferência e nas operações de depósito para verificar se os usuários conhecem as chaves privadas dos compromissos.
Além disso, vamos descrever a verificação Back-Maxwell rangeproof no Solidity:
function verifyRangeProof(
EllipticCurve.ECPoint memory _commitment,
Proof memory _proof
) public view {
require(_proof._c.length == N, "invalid _c length got: ");
require(_proof._s.length == N, "invalid _s length got: ");
EllipticCurve.ECPoint[] memory _r = new EllipticCurve.ECPoint[](N);
for (uint256 _i = 0; _i < N; _i++) {
EllipticCurve.ECPoint memory _sig = EllipticCurve.ecBaseMul(
_proof._s[_i]
);
EllipticCurve.ECPoint memory _p = H.ecMul(pow2(_i));
_p = _proof._c[_i].ecSub(_p);
_p = _p.ecMul(_proof._e0);
_p = _sig.ecSub(_p);
bytes32 _ei = hash(abi.encodePacked(_p._x, _p._y));
_r[_i] = _proof._c[_i].ecMul(uint256(_ei));
}
bytes32 _e0 = hashPoints(_r);
EllipticCurve.ECPoint memory _com = _proof._c[0];
for (uint _i = 1; _i < N; _i++) {
_com = _com.ecAdd(_proof._c[_i]);
}
require(uint256(_e0) == _proof._e0, "failed to verify proof: e0");
require(_com._x == _commitment._x, "failed to verify proof: x");
require(_com._y == _commitment._y, "failed to verify proof: y");
}
É a mesma implementação que você pode explorar no repositório Golang. Antes da verificação, é claro que realizamos verificações do tamanho da prova fornecida por:
require(_proof._c.length == N, "invalid _c length got: ");
require(_proof._s.length == N, "invalid _s length got: ");
O N é o parâmetro constante global que define a ordem do campo de quantidades (2^N).
Além disso, na verificação da prova, estamos usando as chamadas para nossa biblioteca de curvas elípticas, portanto, a seguinte definição deve ser fornecida:
using EllipticCurve for EllipticCurve.ECPoint;
Exemplo de utilização
Para tirar proveito de nosso sistema de ativos confidenciais, primeiro você precisa depositar alguns tokens.
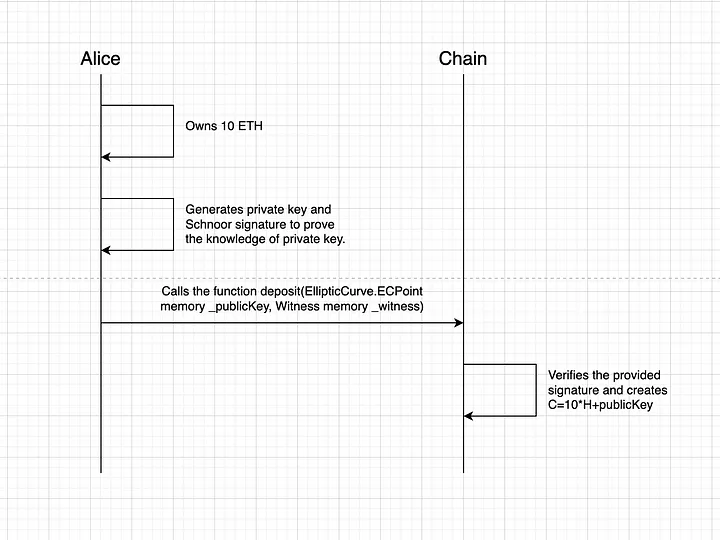
O fluxo de retirada parece ser o mesmo:
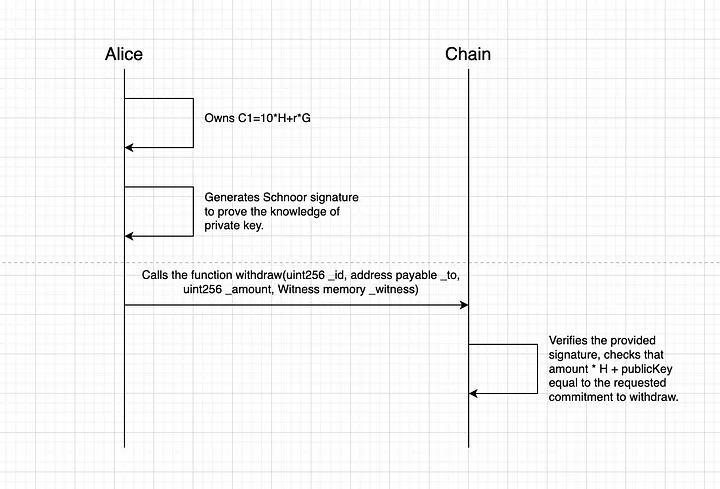
Obviamente, essas transações serão públicas e todos poderão ver quantos tokens foram depositados ou retirados de/para nosso contrato. Mas todas as transferências internas serão realizadas com valores ocultos, de modo que ninguém poderá responder à pergunta quantos tokens você possui ou para quem você enviou dinheiro.
Infelizmente, o fluxo de transferência precisa ser mais complicado para alcançar o anonimato:
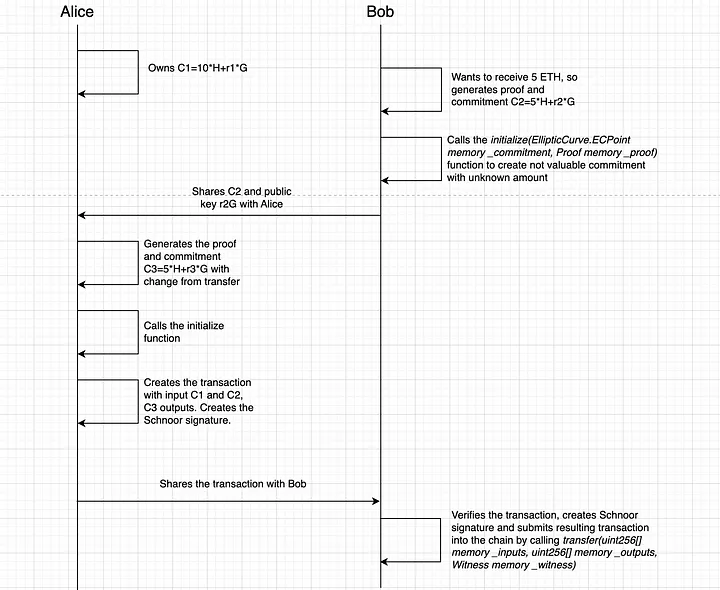
Observe que, durante a transferência, Alice ou Bob devem revelar sua chave pública para o outro lado, o que é necessário para a geração da assinatura Schnoor. À primeira vista, isso leva a uma possível desanonimização do valor do compromisso, mas se você usar várias entradas e saídas, terá que revelar apenas a chave pública agregada e não haverá nenhuma chance de desanonimizar os valores. Por exemplo, no nosso caso, Bob pode usar duas saídas C2_1 = 2H+r2_1G, C2_2 = 3H+r2_2G, em que a soma é igual a 5 ETH, mas somente o compartilhamento de (r2_1 + r2_2)*G é necessário.
A implementação resultante de ativos confidenciais no Solidity pode ser explorada em: github.com/olegfomenko/utxo.
Se tiver dúvidas ou sugestões, envie-me um e-mail para: [email protected]
Artigo escrito por Oleg Fomenko. A versão original pode ser encontrada aqui. Traduzido e adaptado por Dimitris Calixto.

