#Árvore Verkle → A parte 'verge' da Ethereum.
O estágio "Verge" é um dos seis possíveis upgrades no roteiro proposto pelo co-fundador da Ethereum, Vitalik Buterin, para a reformulação da tecnologia blockchain. Ele tem como objetivo abordar o trilema de escalabilidade com o qual a plataforma blockchain continua a lidar. O "Verge" apresenta a ideia da "árvore Verkle" (Verkle tree), que está pronta para substituir as antigas "provas de Merkle/árvore Merkle" (Merkle proofs/Merkle tree). Antes de entrar no conceito da árvore Verkle, é essencial entender a necessidade de tal mecanismo na framework blockchain. Portanto, vamos nos aprofundar nos conceitos básicos, examinando a própria blockchain.
Em uma blockchain, há numerosos blocos alinhados indicando o número de transações verificadas e validadas. Isso está apenas destinado a aumentar com mais participantes/nós se juntando à rede blockchain. Portanto, cada bloco contém um conjunto de dados, incluindo todos os detalhes relacionados às transações. Com a adição de mais blocos à blockchain, há um aumento proporcional no banco de dados também!
Para gerenciar esses enormes bancos de dados e manter a blockchain em funcionamento, o conceito de "estado" entra em cena. O estado inclui os dados do bloco em um formato especializado usando o conceito de árvore Merkle, mantendo todas as contas vinculadas por hashes e, finalmente, reduzindo a um único hash raiz armazenado na blockchain. Esse hash raiz ou a prova de Merkle atua como uma assinatura digital mais forte com um procedimento de verificação simplificado. As provas de Merkle não apenas facilitam o procedimento de verificação de bloco, mas também ajudam a reduzir os requisitos de espaço em disco para realizar transações sem problemas.
Mas desconhecido por muitos, existe uma preocupação oculta com o aumento do tamanho do estado. De acordo com a Ethereum Foundation, o tamanho do estado e as Provas de Merkle juntos já ultrapassaram 135+ gigabytes de espaço de armazenamento. Para superar esse dilema, o estágio "Verge" da atualização da Ethereum propõe a ideia da árvore Verkle. Introduzido por John Kuszmaul em 2018, o conceito de árvore Verkle funciona de forma semelhante à árvore Merkle, mas aqui as provas são menores em tamanho e o tempo de cálculo das provas também é consideravelmente reduzido.
Vamos tentar entender o conceito geral por meio de um exemplo simples.
Geralmente, a árvore Merkle é representada como uma árvore binária, onde o fator de ramificação dos nós é 2. No exemplo discutido aqui, exploraremos um conjunto de 9 transações pertencentes a um bloco adicionado em uma rede blockchain usando uma árvore Merkle k-ária, onde k é o fator de ramificação.
Você sabia que a Ethereum usa uma estrutura hexária em sua Árvore Merkle Patricia (Merkle Patricia Trie)?
A Ethereum usa uma variante da árvore Merkle chamada Árvore Merkle Patricia. Nessa estrutura, cada nó pai pode ter 16 nós filhos. A profundidade média da árvore varia de 10 a 15 níveis e a prova de Merkle requer 15 detalhes de nós irmãos em cada nível.
Portanto, aqui o fator de ramificação selecionado é 3. A primeira etapa aqui envolve o hash de cada uma das transações usando uma função de hash criptográfico. A próxima etapa é agrupar as transações com hash em subconjuntos e gerar um hash a partir dos subconjuntos até que o hash raiz seja calculado. O hash raiz ou prova de Merkle representa o bloco inteiro de transações. A figura abaixo mostra como uma árvore Merkle é construída.
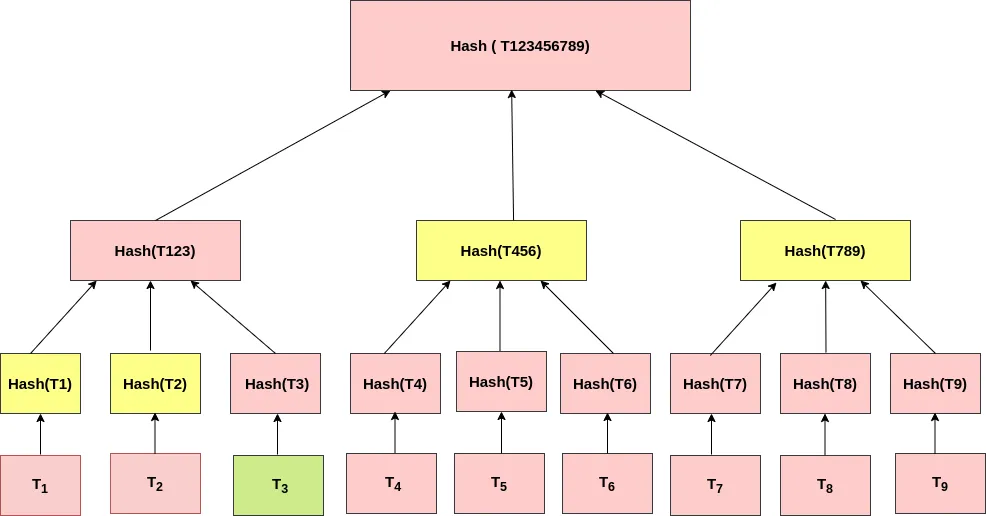
Conforme ilustrado na figura, os hashes dos nós irmãos de T3, ou seja, Hash(T1) e Hash(T2) + hashes concatenados de T4 a T9 podem ajudar cumulativamente a rastrear se T3 pertence a todo o conjunto de transações. E aqui o Hash raiz [ T123456789] é a prova de Merkle que serve como o resumo (footprint) de todo o conjunto de transações.
Continuando, é hora de explorar a árvore Verkle com uma configuração semelhante à anterior. Diferentemente da árvore Merkle, que usa uma função de hash criptográfica para calcular a prova, a árvore Verkle usa o método Vector Commitment (VC) para calcular a mesma. O Vector Commitment é calculado usando as funções polinomiais.
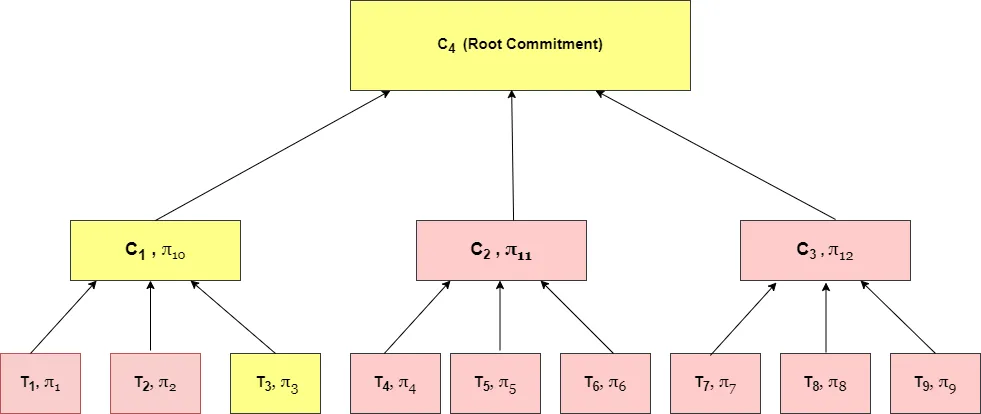
Figura 2: Árvore Verkle de 3 vias
Assim, para uma Árvore Verkle com um determinado número de transações, digamos, T1, T2, T3.....T9, o fator de ramificação da árvore, k (aqui k = 3) é considerado primeiro. O Vector Commitment é então computado em cada um desses subconjuntos. As provas de associação πi para cada transação Ti no subconjunto são computadas com relação ao Compromisso do vetor (observe que i se refere à posição do índice das transações fornecidas). Aqui, C1, C2 e C3 são os compromissos vetoriais resultantes. O compromisso vetorial C4 é calculado sobre esses três compromissos, juntamente com suas provas de associação π10, π11 e π12, respectivamente. Portanto, C4 é o compromisso raiz que forma o resumo da árvore Verkle.
Para compreender melhor, considere a Figura 2, onde (T3,π3) no bloco amarelo significa que a transação T3 existe no compromisso C1 e π3 é a prova dessa existência. Da mesma forma, (C1,π10) significa que o compromisso C1 existe no compromisso raiz C4 e π10 é a prova dessa existência.
Os compromissos de vetor são técnicas criptográficas que permitem comprometer-se com uma sequência ordenada de k valores (t1, t2, ..., tk) de tal forma que seja possível revelar posteriormente um ou vários valores em uma posição específica e provar que eles são consistentes com o compromisso inicial (por exemplo, provar que ti é o i-ésimo valor comprometido). Uma árvore Merkle também é um compromisso de vetor, com a propriedade de que abrir o i-ésimo valor requer um número específico de hashes como prova (prova de Merkle).
A equipe da Ethereum planeja usar o polinômio de compromisso KZG usando um esquema de criptografia de curva elíptica para substituir as funções hash usadas na árvore Merkle.
Assim, para uma árvore com bilhões de pontos de armazenamento de dados, fazer provas de Merkle cumulativas exigiria cerca de 1 kilobyte, mas em uma árvore Verkle a prova seria inferior a 150 bytes. Com a adição de nós, os cálculos de prova de Merkle continuam a se expandir, levando a um aumento na profundidade da árvore Merkle. Ao contrário disso, o tamanho da prova na árvore Verkle permanece constante e a profundidade da árvore é consideravelmente reduzida.
Portanto, enquanto um verificador precisa percorrer múltiplos cálculos de hash em cada nível para chegar à raiz de Merkle, as provas na árvore Verkle simplificam o processo, exigindo fornecer apenas uma única prova em cada nível para chegar ao Compromisso raiz, comprovando assim que uma transação ou um dado faz parte de um determinado conjunto.
Em resumo, a aplicação da árvore Verkle na blockchain pode ser vista abaixo:
Supera os problemas relacionados ao armazenamento de dados: As provas menores nas árvores Verkle resolvem o problema de armazenamento de dados. Por exemplo, no exemplo acima, no caso da árvore Merkle, as provas para a transação T3 são [Hash(T1)+Hash (T2)+ Hash (T456) +Hash (T789)], enquanto as da árvore Verkle são [ π3 + (C1, π10) + C4].
O tempo de verificação é reduzido com provas mais curtas geradas em um período de tempo mais curto, o que permite ainda mais a participação dos validadores da rede.
Implementação de redes de blockchain sem estado.
A eficiência do tamanho da prova da árvore Verkle, por sua vez, ajuda a reduzir o tamanho do nó, o que levará ainda mais à atualização do conceito de cliente sem estado.
Os clientes sem estado ajudam na validação de blocos de execução sem possuir totalmente o estado completo da conta.
As sincronizações de rede serão mais simplificadas.
Promove requisitos de armazenamento sustentáveis.
Tamanhos de prova reduzidos ajudam dispositivos menores a participar como validadores.
Acesso mais rápido às informações (com o compromisso raiz em mãos, os blocos contêm todos os dados necessários para o processamento posterior).
Referências:
1 .Kuszmaul, J. (2019). Verkle trees. Verkle Trees, 1.
2 .https://vitalik.ca/general/2021/06/18/verkle.html
3 .https://nethermind.io/verkle-trees/
4 .https://notes.ethereum.org/@vbuterin/verkle_and_state_expiry_proposal
5 .Campanelli, M., Fiore, D., Greco, N., Kolonelos, D., & Nizzardo, L. (2020). Técnicas de Compromisso vetorial e aplicativos para armazenamento descentralizado verificável. IACR Cryptol. ePrint Arch., 2020, 149
6 .https://blog.ethereum.org/2021/12/02/verkle-tree-structure
7 .https://blog.ethereum.org/2015/11/15/merkling-in-ethereum
8 .https://learn.bybit.com/blockchain/what-is-merkle-tree/
9 https://math.mit.edu/research/highschool/primes/materials/2018/Kuszmaul.pdf
10 .https://cointelegraph.com/explained/merkle-trees-vs-verkle-trees-explained
11 .https://consensys.net/blog/news/the-merge-is-done-whats-next-for-the-ethereum-ecosystem/
12 .Catalano, D., & Fiore, D. (2013). Compromissos vetoriais e suas aplicações. Em Public-Key Cryptography-PKC 2013: 16th International Conference on Practice and Theory in Public-Key Cryptography, Nara, Japão, 26 de fevereiro a 1º de março de 2013. Anais 16 (pp. 55-72). Springer Berlin Heidelberg.
Artigo escrito por Sivadas Neelima e traduzido para o português por Rafael Ojeda
Você pode ler o artigo original aqui

