Conceitos básicos e propriedades
 ######O autor agradece a Benjamin Lehman e Unsplash pela imagem
######O autor agradece a Benjamin Lehman e Unsplash pela imagem
Introdução
Bem-vindo a este guia sobre como construir zk-SNARKs! Zero-Knowledge Succinct Non-Interactive Argument of Knowledge (zk-SNARK ou argumento de conhecimento sucinto não interativo de conhecimento-zero) é uma tecnologia de ponta que oferece privacidade e segurança em sistemas de blockchain. Ele permite verificar a autenticidade de transações sem revelar os detalhes. Neste guia, apresentamos uma visão geral dos zk-SNARKs, suas aplicações e como construí-los.
Você também aprenderá sobre a base matemática por trás dos zk-SNARKs. Por exemplo, aprenderá a gerar o Programa Aritmético Quadrático (QAP) associado a um circuito aritmético. O QAP é o objeto central usado nos zk-SNARKs e sua geração é uma etapa crucial na construção de um zk-SNARK.
Para entender os conceitos matemáticos por trás dos zk-SNARKs, será necessário ter um sólido conhecimento em álgebra, especialmente em campos e grupos.
Ao longo desta série de 3 artigos, também explicaremos as etapas para gerar um QAP, incluindo a representação de um circuito aritmético como um sistema de equações lineares, a conversão do sistema linear em um sistema polinomial e a transformação do sistema polinomial em um QAP.
Esperamos que este guia o ajude a adquirir uma compreensão sólida dos zk-SNARKs e as habilidades necessárias para gerar QAPs manualmente. Este guia fornece o conhecimento e as ferramentas necessárias para construir seus próprios zk-SNARKs e contribuir para o desenvolvimento deste campo empolgante.
Planejamos publicar uma coleção de 3 artigos que esperamos que o ajudem a entender esse conceito. Para ser preciso:
- Postagem 1: a que você está lendo. Aqui, apenas definiremos as principais definições e propriedades: o que é um SNARK e quais são os requisitos para um SNARK. Será curto e fácil de ler, considere-o um aquecimento para o que está por vir.
- Postagem 2: aqui, assumiremos que você conhece o básico (definições e propriedades) dos SNARKs e aprenderá a construir um SNARK para provar conhecimento de um polinômio. Faremos isso passo a passo, partindo de algo que não é um SNARK adequado e terminando em um zk-SNARK completo. A postagem será mais longa e talvez mais difícil de seguir, mas planejamos torná-la fácil de entender.
- Postagem 3: na postagem 3, assumiremos que você é capaz de criar SNARKs para polinômios e estará ansioso para aprender a construir SNARKs para qualquer cálculo. Aqui, você aprenderá como fazer isso. A Postagem 3 é focada em QAPs e, de forma subliminar, R1CSs. Não tão longa quanto a Postagem 2.
Definições
Um SNARK (Argumento de Conhecimento Sucinto e não Interativo) é um protocolo criptográfico entre dois usuários, onde um provador (P) prova a um verificador (V) que um cálculo C está correto. O cálculo é representado por um circuito e o circuito recebe duas entradas: um valor privado chamado testemunha (w) e um valor público (x). O cálculo é considerado correto se a saída C(x, w) for igual a um valor conhecido y.
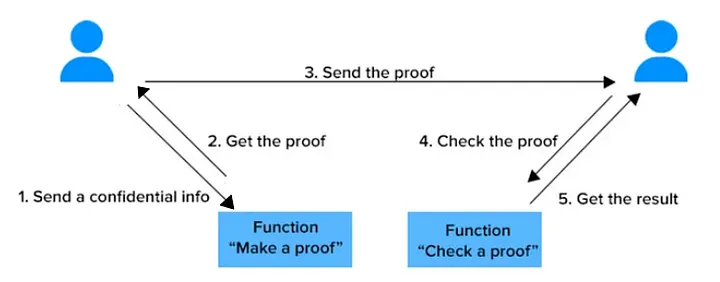
Mais formalmente, um SNARK é um conjunto de três algoritmos: Geração, Prova e Verificação, todos executados em tempo polinomial, de modo que:
- O algoritmo de geração (Gen) recebe como entrada o circuito C e um parâmetro de segurança n. Ele retorna um conjunto de duas chaves, a chave de prova (pk) e a chave de verificação (vk).
- O algoritmo de prova (Proof) recebe como entrada a chave de prova pk associada a C, uma entrada pública x e retorna uma prova π.
- O algoritmo de verificação (Ver) recebe como entrada a prova π, a chave de verificação vk associada a C e a entrada pública x. Ele retorna True ou False dependendo dos resultados do processo de validação.
Propriedades dos SNARKs
Precisamos que as seguintes propriedades sejam satisfeitas por qualquer SNARK:
- Correção: um provador honesto P sempre gerará vk e π de forma que Ver(π, vk, x) = 1 para valores x e w que satisfaçam o circuito C. Em outras palavras, se P for honesto, os algoritmos sempre produzirão provas válidas.
- Robustez: um provador malicioso P que fornece valores para x e w que não satisfazem C tem uma probabilidade negligenciável de gerar uma prova π de forma que Ver(π, vk, x) = 1. Em outras palavras, se P não conseguir executar os cálculos descritos por C, ele não convencerá o verificador V com probabilidade avassaladora.
- Eficiência: o tamanho de π é limitado por um polinômio sobre o parâmetro de segurança n usado em Gen. Esta é a propriedade-chave de concisão.
Se também quisermos gerar um SNARK de conhecimento zero, precisamos de mais uma propriedade:
- Conhecimento zero: o verificador V não é capaz de obter mais detalhes além da saída do algoritmo de verificação Ver.
Conclusão
Este é o fim do nosso primeiro post, onde nos concentramos apenas nos conceitos básicos e propriedades. Como mencionamos na introdução, é apenas um aquecimento para o que está por vir: zkSNARKS para polinômios.
Artigo escrito por Ramsès Fernàndez-València. Traduzido por Marcelo Panegali

