Apresentando QAPs e, subliminarmente, R1CS
O autor agradece a Michael Dziedzic e a Unsplash pela imagem.
Introdução
Este artigo encerra nossa série sobre a construção de SNARKs de conhecimento zero. Ele girará em torno dos conceitos de QAP e R1CS.
Em nossos artigos anteriores, aprendemos as definições e propriedades básicas, e também como construir SNARKs para comprovar o conhecimento de um polinômio. Neste último artigo, aprenderemos a reduzir qualquer computação a um polinômio, para que se possa executar o protocolo SNARK aprendido no segundo artigo.
Programas Aritméticos Quadráticos
Definição
Até este ponto, exploramos como construir zk-SNARKS para comprovar o conhecimento sobre um polinômio. No entanto, nosso objetivo é comprovar a integridade de qualquer computação. Para fazer isso, precisamos converter um programa em um polinômio. A ferramenta necessária para realizar essa conversão é o Programa Aritmético Quadrático (QAP), que apresentamos nesta seção.
Um Programa Aritmético Quadrático (QAP) sobre um campo 𝔉 é uma tupla de polinômios definidos em 𝔉[x]:
junto com um polinômio alvo t(x) ∈ 𝔉[x].
Vamos supor que F seja uma função que recebe n elementos em 𝔉 como entradas e produz n' elementos em 𝔉. Vamos denotar N = n + n', o número total de elementos, contando entradas e saídas.
Dizemos que um QAP, denotado por Q, calcula F se (c_1, …, c_N) ∈ 𝔉^N for uma atribuição válida de entradas e saídas para F, ou seja: se existirem coeficientes (c_{N+1}, …, c_m) tais que t(x) divide o polinômio
Em outras palavras, Q calcula F se for possível encontrar um polinômio h(x) tal que p(x) = h(x) · t(x). O tamanho de Q é m, e o grau de Q é o grau do polinômio alvo t(x).
É possível provar que qualquer circuito aritmético com d produtos e N entradas e saídas resulta em um QAP de grau d e tamanho d + N.
QAPs para Circuitos de Produto
Observação: para o restante deste documento, assumiremos que 𝔉 = ℤ_13.
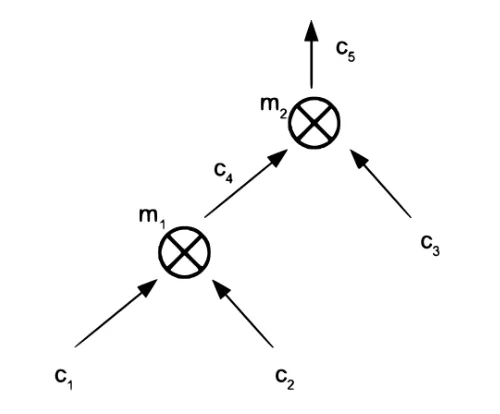
Vamos considerar o circuito abaixo, composto por n = 3 entradas, d = 2 portas de produto m_1 e m_2, uma porta intermediária e n' = 1 saída. Portanto, para o circuito abaixo, m = 5.
A ideia básica por trás da definição de um QAP é acompanhar as variáveis vindas da esquerda e da direita de cada uma das portas de produto. Na figura, a porta m_1 recebe a variável c_1 da esquerda e a variável c_2 da direita, e a porta m_2 recebe a variável c_4 da esquerda e a variável c_3 da direita.
Com essas informações, geramos 3 matrizes, nomeadamente R, L e O, que resumem as informações das variáveis à direita e à esquerda e as saídas, respectivamente. Cada matriz tem tantas linhas quanto variáveis de entrada, intermediárias e de saída, e tantas colunas quanto portas de produto envolvidas no circuito. Por exemplo, no circuito acima, R, L e O serão matrizes de tamanho m x d = 5 x 2.
Como preenchemos essas matrizes depende do papel de cada variável em relação à porta de produto. Por exemplo, nossa matriz L é
Cada coluna corresponde a uma porta de produto: a 1ª coluna para m_1 e a 2ª coluna para m_2. Por outro lado, a i-ésima linha corresponde à variável c_i. Interpretamos a matriz da seguinte maneira: a primeira informa que m_1 recebe apenas c_1 da esquerda (é por isso que o restante da coluna é preenchido com 0s), enquanto a outra informa que m_2 recebe apenas c_4 da esquerda. Da mesma forma, podemos criar matrizes R e O para elementos à direita e saídas, respectivamente:
Observe que O deve ser lido da seguinte forma: m_1 gera a variável c_4 e m_2 gera a variável c_5.
Essas matrizes levam à definição dos conjuntos de polinômios que definem um QAP. Para ser preciso: L é usada para definir o conjunto V, R é usada para definir o conjunto W e O é usada para definir o conjunto Y.
Para definir esses polinômios, precisamos escolher d valores aleatórios, chamados raízes e denotados por r_1, …, r_d. Em nossa situação, d = 2, então escolhemos os valores {2, 3} e as matrizes L, R e O se tornam:
Agora é hora de construir igualdades, usando as informações fornecidas pelo circuito:
Observe que as igualdades acima indicam que v_1(2) = 1 e v_1(3) = 0, e assim por diante. Podemos usar interpolação polinomial para obter v_1(x) = 12x + 3. Da mesma forma, v_4(x) = x + 11 e v_2(x) = v_3(x) = v_5(x) = 0. Portanto o conjunto V usado na definição dos QAPs é
Repetindo o protocolo acima, obtemos os outros dois conjuntos:
Estamos quase terminando o cálculo do polinômio p(x). A única coisa que resta fazer é encontrar os valores c_1, …, c_m correspondentes a entradas e saídas válidas para o circuito. Isso pode ser feito ao escolher valores aleatórios para as entradas c_1, c_2 e c_3 e calcular c_4 e c_5 seguindo as regras do circuito. Vamos considerar c_1 = 2, c_2 = 3 e c_3 = 4. Então
c_4 = m_1(c1, c2) = c_1 · c_2 = 6 e
c_5 = m_2(c_4, c_3) = c_4 · c_3 = 6 · 4 = 24 ≡ 11 (mod 13)
Assim, o conjunto de entradas e saídas válidas é {2, 3, 4, 6, 11}. Portanto:
Por fim, precisamos encontrar o polinômio alvo que divide p(x). Vamos ter em mente os polinômios v_i(x), w_i(x) e y_i(x), uma vez que foram usados na definição de p(x), portanto, avaliar p(x) nos valores r_1 = 2 e r_2 = 3 resultará em 0, significando que:
QAPs para Circuitos Aritméticos
Até agora, aprendemos como construir o QAP associado a um circuito envolvendo apenas produtos. Nesta seção, estenderemos as técnicas para circuitos "aritméticos", envolvendo produtos e adições.
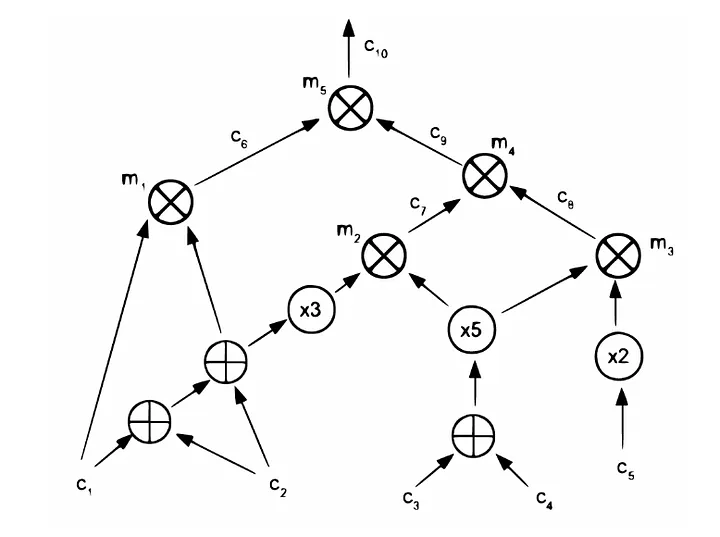
A partir de agora, trabalharemos no seguinte circuito com n = 5 entradas, d = 5 portas de produto, 4 portas intermediárias e n' = 1 saída. Portanto, neste caso, m = 10.
Observamos que, como na seção anterior, os únicos elementos que contam para rotular e deduzir o valor de m são as entradas "externas" e as saídas das portas de produto.
Observação: como a ideia por trás da geração do QAP é a mesma da seção anterior, algumas das computações serão omitidas.
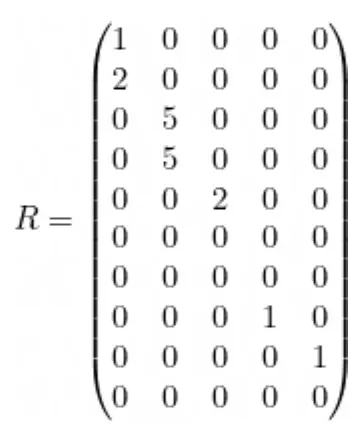
Agora, levamos em consideração as variáveis vindas da esquerda, da direita e as saídas para construir as matrizes L, R e O. Observamos que o tamanho das matrizes é m x d = 10 x 5.
Agora precisamos considerar não apenas as variáveis vindas da direita ou da esquerda, mas também o "peso" de cada variável. Observamos que m1 recebe da direita o resultado de fazer c_1 + 2c_2, portanto, m_1 recebe um c_1 e dois c_2 da direita.
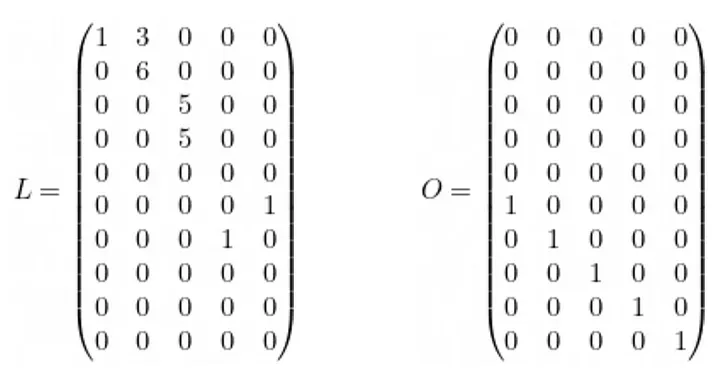
Da mesma forma, podemos calcular as matrizes correspondentes à esquerda e às saídas:
Agora é a vez de escolher d = 5 valores aleatórios, por exemplo, {0, 1, 2, 3, 4} e considerar as matrizes:
Se agora considerarmos as igualdades entre as matrizes à esquerda, à direita e de saída, podemos então aplicar interpolação para obter cada polinômio:
Agora podemos calcular o polinômio p(x). Como feito na seção anterior, calcularemos os valores c_i escolhendo valores aleatórios para c_1, c_2, c_3, c_4, c_5 e calculando os valores c_6, c_7, c_8, c_9, c_10 substituindo os anteriores no circuito. Fazendo isso, obtemos o conjunto {c_1, …, c_10} = {2, 3, 5, 6, 7, 3, 7, 3, 8, 11}, então o polinômio p(x) é:
Para concluir o protocolo, precisamos construir o polinômio h(x). Como p(x) tem raízes {0, 1, 2, 3, 4}, o polinômio t(x) será:
Conclusões
SNARKs de conhecimento zero são um tipo de prova criptográfica que permite a verificação da autenticidade de computações sem revelar suas entradas. Se essa computação representar a verificação de transações da blockchain, podemos processar transações da blockchain sem revelar seus detalhes. Isso proporciona um alto grau de privacidade e segurança em sistemas de blockchain.
Apresentamos um guia autocontido para zk-SNARKs que começa com o conceito em si e termina com o procedimento passo a passo para construir o zk-SNARK de um circuito aritmético arbitrário. A principal motivação para criar este guia foi fornecer um manual para um tópico que é onipresente em blockchain. Também é bastante desafiador abordar, pois as pessoas tendem a articular sua compreensão de um campo que é, em grande parte, uma arte matemática.
Na blockchain, zk-SNARKs também são usados para permitir transações anônimas, onde a identidade das partes envolvidas permanece oculta, ao mesmo tempo em que permite à rede verificar que as transações são válidas.
Além disso, zk-SNARKs permitem aumentar a escalabilidade da blockchain, reduzindo os requisitos computacionais e de armazenamento dos sistemas de blockchain, o que é um desafio significativo para os protocolos tradicionais de blockchain.
Em geral, zk-SNARKs desempenham um papel crucial no desenvolvimento e implementação de sistemas de blockchain preservadores de privacidade e escaláveis, sendo uma ferramenta fundamental para viabilizar o futuro das finanças descentralizadas e outras aplicações baseadas em blockchain.
Referências
- Rosario Gennaro, Craig Gentry, Bryan Parno e Mariana Raykova, Programas de Span Quadrático e NIZKs Concisos sem PCPs, Cryptology ePrint Archive, Paper 2012/215.
- Jordi Herrera Joancomartí, Cristina Pérez Solà, Criptografia Avançada. Notas de aula. Universidade Aberta da Catalunha, 2022.
Artigo escrito por Ramsès Fernàndez-València. Traduzido por Marcelo Panegali.



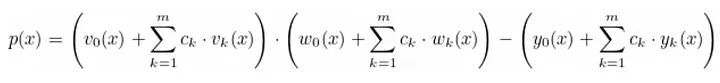
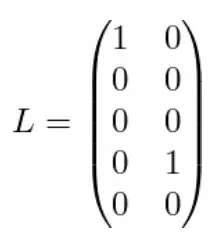
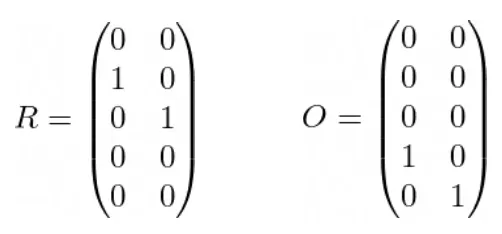
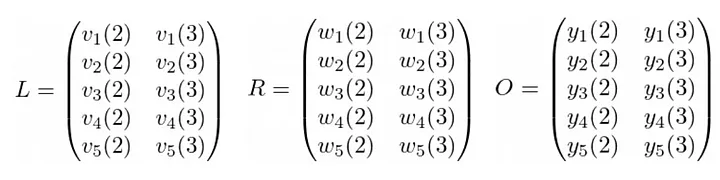
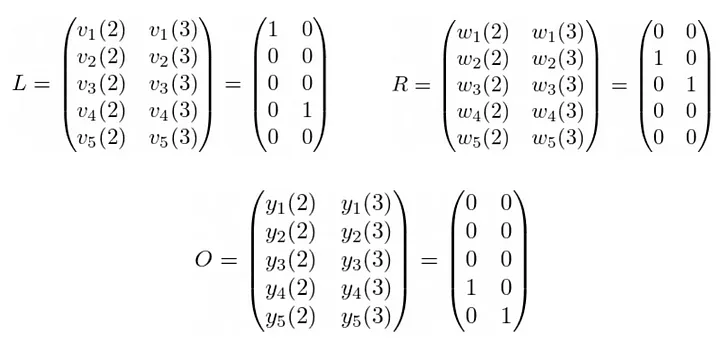
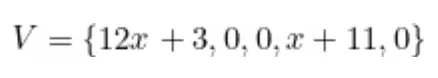
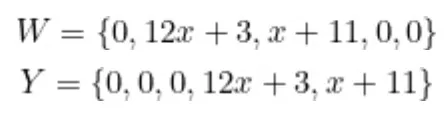
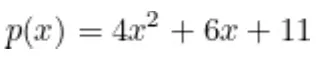
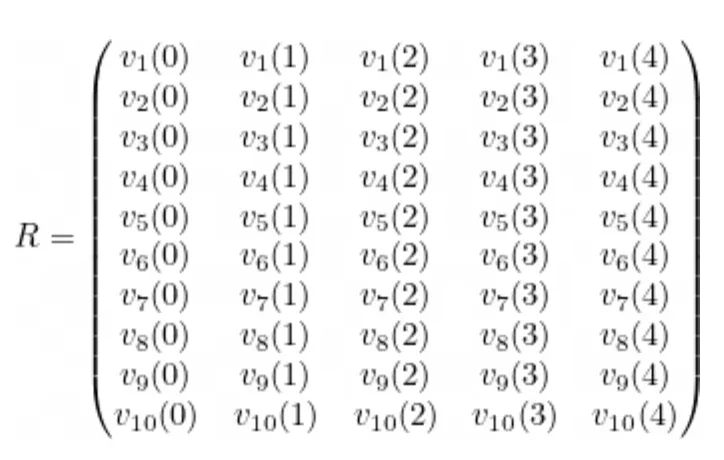
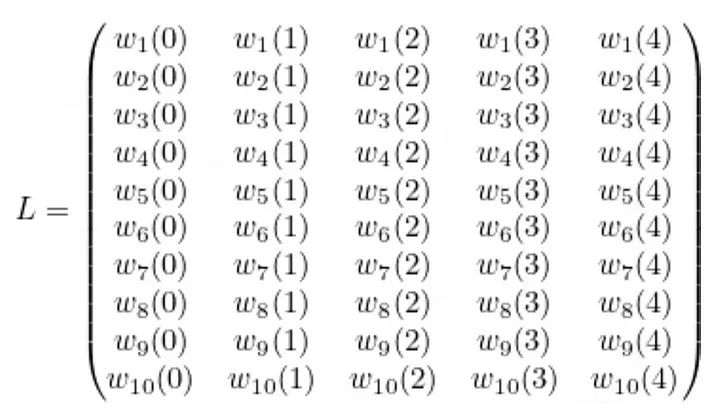
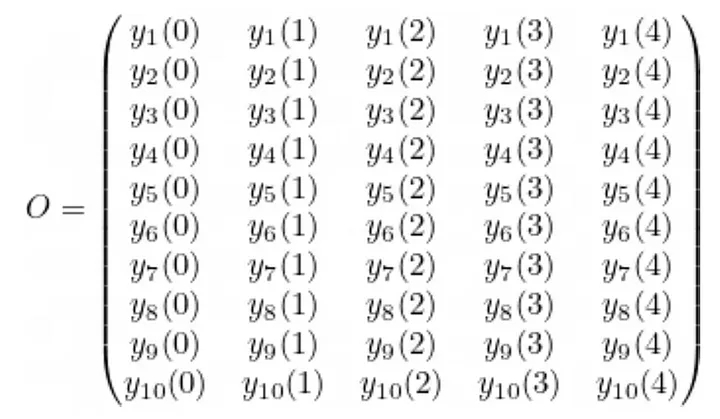
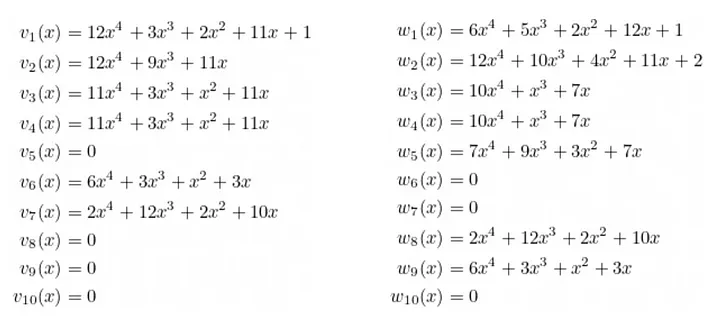
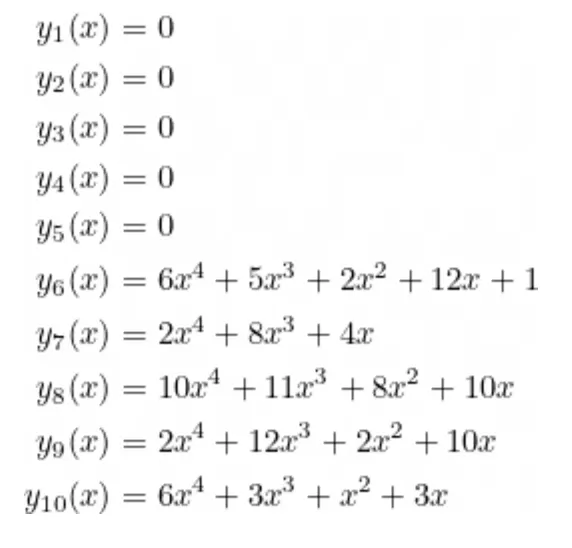
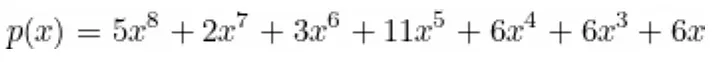







Oldest comments (0)