O firmware da Trezor é de código aberto. Sua biblioteca criptográfica é amplamente utilizada por empresas como a TrustWallet para gerar carteiras em Bitcoin e Ethereum. Vamos examinar como a biblioteca criptográfica Trezor gera frases-semente mnemônicas para Bitcoin e Ethereum.

Um exemplo de frase-semente mnemônica.
Se você ainda não sabe, as frases-semente mnemônicas são extraídas de uma lista de palavras bem definida contendo 2048 palavras. A geração segura de frases mnemônicas é uma função de como você indexa nessa lista de palavras para depois selecionar palavras dela. Como existem 2048 palavras, você precisa de 11 bits para alcançar todas as palavras possíveis.
A primeira função que o firmware Trezor chama para gerar uma frase-semente mnemônica é mnemonic_generate(), que aceita uma força (a quantidade de entropia a ser codificada, onde 256 bits produzem uma frase de 24 palavras). Esta função finalmente retorna o array de caracteres que é sua frase-semente mnemônica.

A primeira função chamada na geração da frase mnemônica
uint8_t data[32] é passado para a função random_buffer(), cujo trabalho é preenchê-lo com bytes gerados aleatoriamente.
A função random_buffer() tem a seguinte aparência, onde uint8_t *buf é nosso data array, e size_t len, seu comprimento (32).

Função random_buffer()
Como cada índice no array armazena 8 bits, cada 4 índices armazenam 32 bits. O loop for mostra que a cada 4 índices no array, atribuímos à variável r o valor de retorno da função random32(), cujo trabalho é retornar um valor aleatório de 32 bits.
Essa função random32() é a última função chamada na biblioteca Trezor para gerar aleatoriedade. O que quer que o random32() faça - seja retornar sempre os mesmos 32 bits ou extrair números de um gerador aleatório e criptograficamente seguro - é o que será usado para selecionar palavras para a lista de palavras BIP39.
Por padrão, o arquivo rand.c contendo a função random32() informa:
#pragma message( \ "NOT SUITABLE FOR PRODUCTION USE! Replace random32() function with your own secure code.")
// O código a seguir não deve ser usado em um ambiente de produção. Ele está incluído apenas para tornar a biblioteca testável.
// A mensagem acima tenta evitar qualquer uso acidental fora do ambiente de teste.
//
// Você deve substituir a função random8() e random32() por seu próprio código seguro. Há também a possibilidade de substituir a função random_buffer(), pois ela é definida como um símbolo fraco.
Assim, a biblioteca Trezor exige que você, o usuário da biblioteca, forneça sua própria fonte de aleatoriedade substituindo a definição da função random32().
Para esse efeito, a implementação padrão de random32() no repositório do firmware Trezor não é adequada para uso em produção. Ela produz números previsíveis, produzindo sempre a mesma frase-semente.
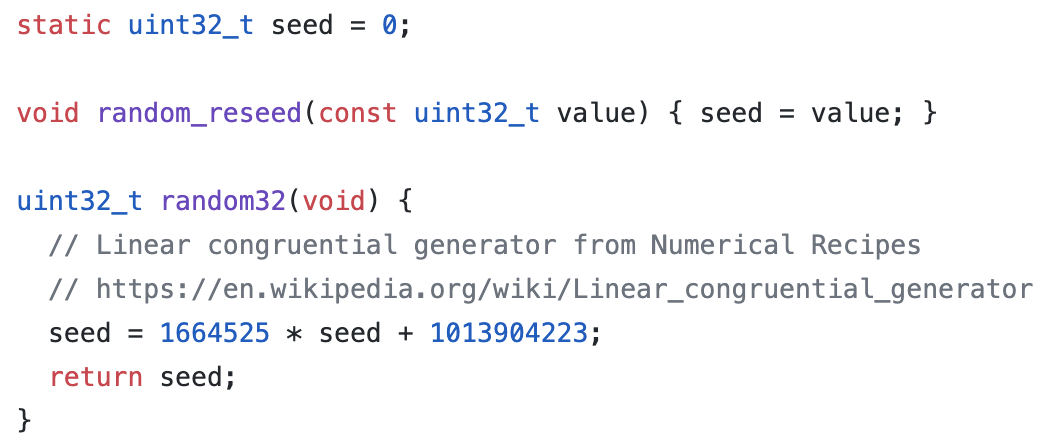
A implementação padrão de random32(), deixada para o usuário alterar.
Supondo que você substitua esta função por um gerador de números aleatórios criptograficamente seguro, podemos reexaminar a função random_buffer():

Função random_buffer()
A linha na parte inferior copia o valor aleatório de 32 bits atribuído a r no array buff um byte por vez.
buf[i] = (r >> ((i % 4) * 8)) & 0xFF;
Vamos percorrer uma iteração:
Quando i = 0 , r (o valor aleatório de 32 bits) é deslocado para a direita por ((i % 4) * 8) bits, que é ((0) * 8) ou 0 bits. O resultado disso é seguido de AND com 0xFF, que sempre resulta no último byte de tudo o que você está adicionando ao AND sendo mantido.
Assim, quando i = 0, o último byte desse valor aleatório de 32 bits é colocado no índice 0 do array buf. Quando i = 1, esse valor aleatório de 32 bits é deslocado para a direita em 8 bits, então seguido de AND com 0xFF. Isso significa que buff[1] conterá o penúltimo byte desse valor aleatório. Isso continua até que o valor completo de 32 bits seja armazenado nos índices 0–3 e um novo valor aleatório de 32 bits seja escolhido quando i = 4.
Após random_buffer() retornar o array de valores aleatórios de 32 bits, passamos para mnemonic_from_data(), que aceita esse array e seu comprimento (32).

Função mnemonic_from_data(), que recebe bytes aleatórios e retorna a frase mnemônica.
Essa função primeiro cria um array de bytes chamado bits, de comprimento 32 + 1 (33). Esse array, juntamente com o data array e seu comprimento, é passado para a função sha256_Raw(), que gera um hash SHA256 dos bytes aleatórios no data array e o coloca dentro do recém-criado array bits.
Depois que essa função retornar, você verá a linha:
// soma de verificação
bits[len] = bits[0]
Você notará que o array bits é de tamanho 32 + 1. Esse 33º byte (índice 32 no array) se torna parte dos dados usados para selecionar a 24ª palavra da frase mnemônica.
Ao gerar uma frase-semente mnemônica de 24 palavras, a 24ª palavra não é selecionada como as 23 anteriores. Em vez disso, parte dela vem de uma soma de verificação (checksum) das outras 23 palavras. Especificamente, o primeiro byte da soma de verificação dos 32 bytes aleatórios que geramos é anexado ao final desse array. Para esse efeito, bits[len] recebe o valor de bits[0], que é o primeiro byte da soma de verificação.
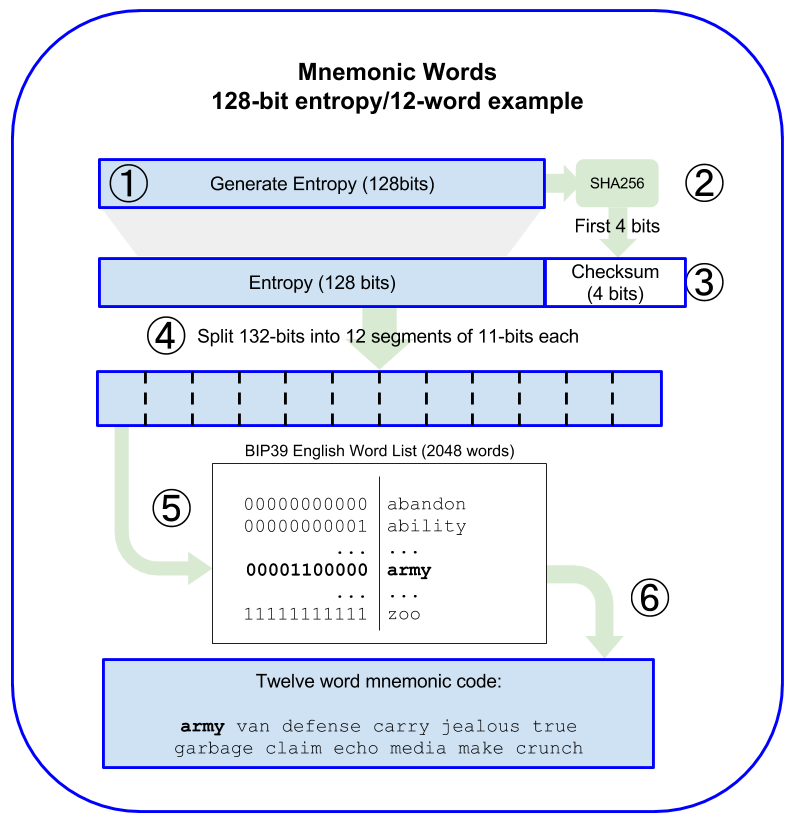
Diagrama demonstrando como a soma de verificação é anexada, de “Mastering Ethereum” de Andreas Antonopolous
A próxima linha copia os 32 bytes de dados aleatórios do data array para os primeiros 32 índices (índices de 0 a 31) do array bits.
// dados
memcopy(bits, data, len)
Agora, o array bits contém os 32 bytes aleatórios que geramos anteriormente nos índices 0–31 e o primeiro byte de sua soma de verificação no índice 32. Isso é um total de 33 bytes, que também é 264 bits.
Como mencionei anteriormente, precisamos de 11 bits para poder selecionar qualquer palavra de uma lista de palavras contendo 2048 palavras. Dividindo os 264 bits de dados que temos do requisito de 11 bits por palavra, você obtém 24 palavras. Assim, temos todos os dados necessários para criar nossa frase mnemônica de 24 palavras selecionada aleatoriamente.
Na próxima seção desta função explico como o firmware Trezor converte nosso array bits em índices na lista de palavras:

A equipe da Trezor nomeou o array de bytes como bits, porque é tratado como um agrupamento de 11 bits por vez. Cada 11 bits representa um índice na lista de palavras BIP39.
O loop externo vai de 1 a mlen, que foi declarado anteriormente como o comprimento de nossa frase mnemônica, 24. O loop interno itera 11 bits por vez, convertendo-os em um valor inteiro aumentando a variável idx. Essa variável é então usada para selecionar uma palavra da lista de palavras.
Quando i = 0 (ou seja, estamos selecionando a primeira palavra do nosso mnemônico de palavras), o idx é primeiramente definido como 0. No loop interno, temos j = 0, significando que estamos avaliando o primeiro bit dos primeiros 11 bits no array bits.
A primeira coisa que vemos é idx <<= 1. Este é um operador de atribuição de deslocamento à esquerda, que significa deslocar o idx para a esquerda em um bit e, em seguida, armazenar o resultado de volta no idx. Uma explicação mais simples: você está multiplicando o idx por 2. Vou explicar por que isso está sendo feito em breve.
A próxima linha é mais envolvente. Antes de continuar lendo, entenda que a razão desta próxima linha existir é porque estamos tentando examinar um array onde cada índice tem apenas 8 bits de comprimento, 11 bits por vez.
O array bits pode ter a seguinte aparência:

Como pode ser o array bits.
Mas, como queremos tratar esse array como agrupamentos de índices de 11 bits, um índice completo se espalha por vários elementos no array bits:

Considerando 11 bits por vez, do array de bytes chamado bits.
Tendo isso em mente, a linha é:
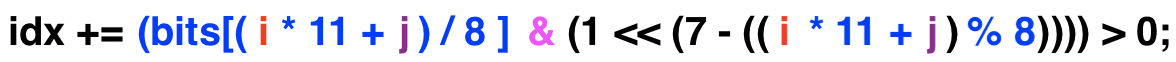
Verificando se deseja adicionar 1 ao idx.
A primeira parte desta equação é bits[(i * 11 + j) / 8 ]. Isso retorna o byte no bits[], que contém o bit específico que estamos examinando. Veja como isso funciona:
Como cada índice é representado por 11 bits, i * 11 + j representa o “índice absoluto” do array bit que está sendo examinado. Há um total de 264 bits neste array. Se i = 0 e j = 5, esta parte da equação retorna bits[(0 * 11 + 5 / 8)] = bits[5 / 8] = bits[0], o byte onde o 6º bit reside.
Adicionamos AND a esse byte específico com o resultado do lado direito do operador &, que cria, do zero, um byte diferente.
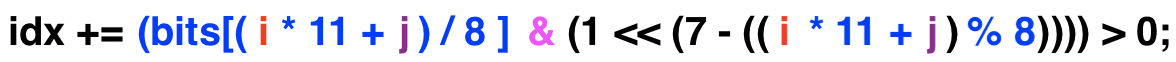
A mesma equação anterior
Este novo byte sendo criado no lado direito do & será composto somente por 0s, exceto para o bit específico que estamos examinando, apontado como j.
O lado direito do & tem a seguinte aparência:
1 << 7 - ((i * 11 + j) % 8)
Isso pega o índice absoluto do bit em i * 11 + j, descobre o quão longe em um byte específico seria fazendo % 8, então subtrai esse valor de 7 e desloca 1 para a direita por esse número de bits. A intenção é descobrir quantos 0 bits precisam ser adicionados à direita desse 1 bit para criar um novo byte, que tenha esse 1 bit específico se alinhando exatamente onde o bit que estamos examinando no byte foi retornado à esquerda de &.
Vimos que se conectarmos i = 0 e j = 5, é retornado bits[0] no lado esquerdo do &. Vamos supor que bits[0] é 0b00101000.
Conectando esses valores i e j no lado direito do & você obtém:
1 << (7 - ((0 * 11 + 5) % 8)
= 1 << (7 - (5 % 8))
= 1 << 7 - (5)
= 1 << 2
= 0b00000100 // Um byte diferente criado do zero
Criamos um novo byte do zero, com um bit 1 no índice 5 (o 6º bit no byte).
Agora, podemos finalmente adicionar & nos lados esquerdo e direito:
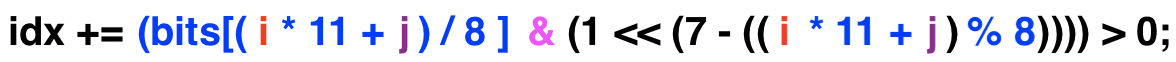
A mesma equação anterior
O lado esquerdo era 0b00101000. O lado direito é 0b00000100.
0b00100100 // bits[0]
AND
0b00000100 // O byte criado do zero, com um "1" no bit "j"
=
0b00000100
Se esta operação AND produz um byte composto somente por 0s, sabemos que esse bit não foi definido no array bits (o byte sendo examinado no lado esquerdo do &). Se o resultado não for composto somente por 0s, sabemos que um 1 estava presente naquele local do array bits.
No nosso caso, esse resultado não foi composto somente por 0s, o que significa que o bit do array bits que está sendo examinado foi definido como 1. O resultado deste & é um valor maior que 0, significando que a verificação final da extrema direita da equação > 0 avalia como 1 (ou verdadeiro).
Como a verificação > 0 é avaliada como 1, o idx é incrementado em 1. O loop interno j prossegue para cada bit restante nos 11 bits que estamos considerando.
A linha idx <<= 1 de antes deve fazer mais sentido agora. Cada vez que um bit está presente no array bits, 1 é adicionado ao idx. Esse 1 precisa ir para seu local apropriado dentro do idx.

Considerando 11 bits por vez, do array de bytes chamado bits
Se o bit 0 da palavra 0 for definido como 1, então esse 1 realmente representa 210. Se o 3º bit for definido, como na imagem acima, ele realmente representa 2⁸. Este idx <<= 1 converte a representação binária desses 11 bits em um integer usando o loop interno j para multiplicar idx por 2 quantas vezes forem necessárias.
Depois que o loop j termina, o passo final é:

Extraindo a palavra da lista de palavras
Isso pega o integer produzido a partir dos 11 bits e o usa para indexar na wordlist (lista de palavras). Essa palavra é copiada para p, um ponteiro para o início do array de caracteres anteriormente declarado para armazenar o mnemônico.
p é incrementado pelo tempo que a palavra esteve na linha p += strlen(wordlist[idx]). Se esta não for a 24ª palavra, um espaço (' ') é adicionado a p para separar visualmente esta palavra da próxima palavra no mnemônico quando ele for retornado ao usuário. Se for a 24ª palavra, um 0 é adicionado, denotando o final da string.
Depois que i e j constroem 24 índices iterando sobre esse array 11 bits por vez, a frase mnemônica é gerada e retornada ao usuário.
Conclusão
O caminho que descrevi neste post funciona como esperado. Com isso dito:
- É desaconselhável fornecer uma implementação padrão de uma biblioteca de criptografia que seja completamente insegura. O histórico do git mostra que uma vez o random32() puxou de
/dev/urandom, e outra vez usou um timestamp previsível como semente. Uma exceção é a única opção correta aqui, independentemente de permitir que os usuários “testem” a biblioteca quando quiserem. - O código que mostrei para gerar índices de 11 bits é extremamente ineficiente. Ele faz dezenas de operações para iterar bit a bit o que poderia ser feito facilmente palavra por palavra na memória, mascarando 11 bits por vez. Isso é estranhamente justaposto com o uso explícito de um operador de atribuição de deslocamento à esquerda, quando qualquer compilador moderno otimizaria uma multiplicação mais legível por 2.
O histórico do git foi interessante de se ver. Eu encorajo você a ler por si mesmo.
Artigo publicado por Brandon Arvanaghi em 7 de maio de 2019, traduzido por Paulinho Giovannini. Você pode encontrar a publicação original aqui.

