Analisamos como os protocolos DeFi facilitam a tomada e a concessão de empréstimos.
Este artigo é o primeiro de uma série de três, que discute como funcionam os protocolos de empréstimo DeFi - seus principais componentes, fórmulas e casos de uso. Ao fazer isso, destacaremos como, apesar das nomenclaturas diferentes e criativas, os protocolos tendem a reutilizar, iterar e compartilhar conceitos fundamentais. Uma dessas implementações compartilhadas, sobre a qual escrevemos detalhes nesta publicação do blog, é o uso de tokens ERC20 para representar a participação de um usuário em Lending Pools (Pools de Empréstimo). Começaremos destacando os elementos conceituais exclusivos desses protocolos e forneceremos conceitos técnicos para identificar como eles funcionam.
Pools de Empréstimo
Nas finanças tradicionais (ou TradFi), a concessão e tomada de empréstimos eram mediados por instituições financeiras terceirizadas. Essas instituições financeiras eram encarregadas de duas tarefas principais: impor o pagamento de juros pelas partes mutuárias às partes mutuantes e avaliar e impedir que as partes consideradas não confiáveis participassem dessas atividades.
Por outro lado, no financiamento descentralizado (ou DeFi), não se pode confiar em credores e tomadores de empréstimos terceirizados. Essa ausência de confiança inspirou um novo projeto para facilitar os processos de empréstimo on-chain.
Um pool de empréstimos é um contrato inteligente. Os usuários do protocolo DeFi podem depositar ativos (geralmente tokens ERC20), com o objetivo de usar esse contrato para emprestar os ativos depositados. Outros usuários podem interagir com os pools de empréstimos para usufruir de empréstimos imediatos - tomando emprestado contra ativos como garantia, depositados no pool.
Os pools de empréstimos têm algumas vantagens importantes relacionadas a empréstimos e financiamentos, em comparação com os métodos financeiros tradicionais. Por exemplo:
- Com o DeFi, os empréstimos não são limitados pela disponibilidade de 1:1 de fundos de empréstimo para o valor emprestado. Em vez disso, os fundos de todos os usuários do protocolo são depositados no pool, criando assim um estoque de tokens suficientemente grande para acomodar os empréstimos imediatamente.
- O DeFi elimina os cronogramas de pagamento. Os empréstimos são executados contra garantias previamente depositadas e os usuários podem optar por pagar a qualquer momento.
A esta altura, você deve estar se perguntando: "Por que eu tomaria emprestado ativos em um protocolo de empréstimo se tenho de fornecer ativos de igual valor (ou até mesmo supervalorizados) como garantia? Em vez disso, eu não deveria vender a garantia e comprar os ativos emprestados?"
Bem, o fato de os protocolos de empréstimo DeFi parecerem permitir apenas empréstimos totalmente (ou mais) garantidos abre a porta para uma metodologia de "negociação" interessante: a alavancagem.
Imagine que você está otimista com o WBTC - 100% certo de que seu valor vai disparar! Você poderia depositar um pouco de WBTC (digamos, no valor de US$ 1.000) em seu protocolo de empréstimo favorito, usá-lo para tomar emprestado um pouco de stablecoin (ou seja, USDC) com o qual você poderia comprar ainda mais WBTC (para o nosso cenário, digamos, metade do seu depósito inicial - US$ 500) em alguma exchange. Nesse cenário, você teria US$ 1.500 expostos ao WBTC, a partir de seus US$ 1.000 iniciais.
Mas espere, tem mais! E se você depositasse o valor de US$ 500 em garantia do WBTC para tomar emprestado ainda mais USDC contra ele? Esse processo é conhecido como superalavancagem e você poderia fazer isso repetidamente até que a política do protocolo o impeça de fazer isso, uma vez que você tenha excedido seu poder de empréstimo.
Em um cenário semelhante, digamos que você esteja pessimista em relação ao WBTC (afinal, estamos no inverno criptográfico ❄️). Você poderia fazer o oposto do cenário anterior e depositar USDC como garantia para tomar emprestado o WBTC, do qual se livraria imediatamente para comprar mais dessa stablecoin. Se sua previsão se concretizar e o preço do WBTC cair, você poderá comprar a mesma quantia emprestada por um preço mais baixo em uma bolsa, pagar seu empréstimo e ficar com o excesso de USDC, abrindo (e fechando) uma posição de venda no WBTC!
“Share Tokens”
Assim como no TradFi, os usuários que depositam seus ativos em pools de empréstimos são incentivados a manter seus fundos no pool a longo prazo, com juros sobre seus depósitos. Os juros são acumulados ao longo do tempo, calculados como uma porcentagem do depósito de um usuário no pool de empréstimos pelo protocolo e reivindicados pelo respectivo usuário depositante. Quanto mais tempo um usuário mantiver seus ativos em um pool de empréstimos, mais juros serão acumulados.
Como o protocolo contabiliza a participação de cada usuário no pool? Lembre-se de que, quando um usuário deposita ativos no pool, sua "participação" dilui a de todos os usuários e o protocolo reflete isso adequadamente. No entanto, o protocolo não rastreia e atualiza a participação de cada usuário no pool em cada instância de retirada ou depósito diretamente. Fazer isso on-chain seria um desperdício imenso e proibitivamente caro para os depositantes, que pagariam a conta de cada execução de atualização.
Em vez disso, o protocolo foi projetado para lidar apenas com a alteração na participação do depositante sem precisar atualizar ativamente as participações de outros usuários.
Você pode pensar que esse protocolo permite que você tenha seu bolo e o coma também. Mas não é bem assim:
Os protocolos lidam com a emissão de juros, cunhando e queimando tokens ERC20, aos quais nos referiremos como "Share Tokens", que representam a participação de um credor (ou proporção de ativos depositados) em seu pool de empréstimos. Esse projeto de "Share Tokens" ajusta automaticamente a diluição das ações de outros "shareholders" (acionistas) para refletir a cunhagem e queima de "shares" (ações), proporcional ao depósito ou retirada de seus ativos subjacentes, respectivamente.
A seguir, forneceremos exemplos reais de como diferentes protocolos empregam "Share Tokens" e discutiremos suas semelhanças.
aToken: “Share Token” do AAVE
aTokens são os tokens geradores de rendimento do AAVE, cunhados e queimados pelo pool de empréstimos ao depositar e retirar ativos do protocolo ou para ele, respectivamente.
Os aTokens são tokens do tipo ERC20 integrados ao protocolo AAVE, de modo que há um aToken para cada um dos mercados em que um usuário possa entrar (depositar garantias).
Se dermos uma olhada no contrato do pool de empréstimos do AAVE, poderemos ver as operações subjacentes que acontecem quando um usuário deposita ativos no pool:
pragma solidity ^0.8.13;
function deposit(
address asset,
uint256 amount,
address onBehalfOf,
uint16 referralCode
) external override whenNotPaused {
DataTypes.ReserveData storage reserve = _reserves[asset];
ValidationLogic.validateDeposit(reserve, amount);
address aToken = reserve.aTokenAddress;
reserve.updateState();
reserve.updateInterestRates(asset, aToken, amount, 0);
IERC20(asset).safeTransferFrom(msg.sender, aToken, amount);
bool isFirstDeposit = IAToken(aToken).mint(onBehalfOf, amount, reserve.liquidityIndex);
if (isFirstDeposit) {
_usersConfig[onBehalfOf].setUsingAsCollateral(reserve.id, true);
emit ReserveUsedAsCollateralEnabled(asset, onBehalfOf);
}
emit Deposit(asset, msg.sender, onBehalfOf, amount, referralCode);
}
Podemos ver que o aToken correspondente ao mercado em que o usuário depositou será chamado, com a função mint.
pragma solidity ^0.8.13;
function mint(
address user,
uint256 amount,
uint256 index
) external override onlyLendingPool returns (bool) {
uint256 previousBalance = super.balanceOf(user);
uint256 amountScaled = amount.rayDiv(index);
require(amountScaled != 0, Errors.CT_INVALID_MINT_AMOUNT);
_mint(user, amountScaled);
emit Transfer(address(0), user, amount);
emit Mint(user, amount, index);
return previousBalance == 0;
}
Como podemos ver, o valor real a ser cunhado é:
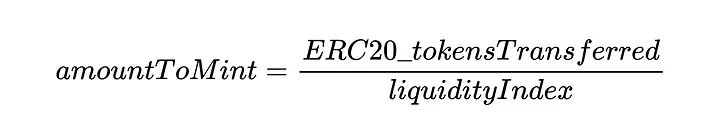
Em nosso exemplo, o usuário entrou em um mercado cuja reserva (ou pool) já havia acumulado alguns juros sobre seus ativos depositados anteriormente. A equação acima nos ajuda a entender isso, pois mostra como contabilizar o acúmulo de juros de todos os usuários com um índice global que é atualizado em várias ações (depósitos, retiradas etc.).
Quando o usuário retira seu ativo subjacente, o liquidityIndex é usado como um multiplicador para calcular o número de tokens devidos na transação.
Abaixo está o trecho de código relevante do contrato do pool de empréstimos:
pragma solidity ^0.8.13;
function withdraw(
address asset,
uint256 amount,
address to
) external override whenNotPaused returns (uint256) {
DataTypes.ReserveData storage reserve = _reserves[asset];
address aToken = reserve.aTokenAddress;
uint256 userBalance = IAToken(aToken).balanceOf(msg.sender);
uint256 amountToWithdraw = amount;
if (amount == type(uint256).max) {
amountToWithdraw = userBalance;
}
ValidationLogic.validateWithdraw(
asset,
amountToWithdraw,
userBalance,
_reserves,
_usersConfig[msg.sender],
_reservesList,
_reservesCount,
_addressesProvider.getPriceOracle()
);
reserve.updateState();
reserve.updateInterestRates(asset, aToken, 0, amountToWithdraw);
if (amountToWithdraw == userBalance) {
_usersConfig[msg.sender].setUsingAsCollateral(reserve.id, false);
emit ReserveUsedAsCollateralDisabled(asset, msg.sender);
}
IAToken(aToken).burn(msg.sender, to, amountToWithdraw, reserve.liquidityIndex);
emit Withdraw(asset, msg.sender, to, amountToWithdraw);
return amountToWithdraw;
}
Aqui, a função balanceOf do contrato aToken é estranha! Afinal de contas, acabamos de estabelecer que a quantidade de aTokens cunhados se desvia do valor dos ativos subjacentes depositados. Como é possível que chamando IAToken(aToken).balanceOf(address(user))renda o valor dos ativos subjacentes a serem retirados (conforme visto na parte inferior da função)? Bem:
- Quando um usuário retira seus ativos, seus
aTokenssão queimados. EssesaTokensqueimados mantêm a quantidade total deaTokensque outros usuários possuem proporcional à sua participação no pool, após a retirada dos ativos dos usuários. - As taxas de juros do mercado do qual um usuário retira seus fundos são atualizadas a cada retirada.
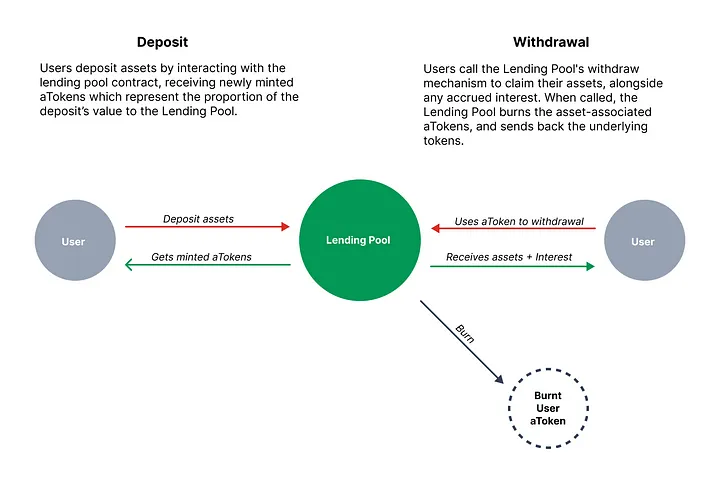
Como estabelecemos anteriormente, os aTokens são tokens semelhantes ao ERC20. Enfatizamos que eles são "semelhantes" aos tokens ERC-20 devido às propriedades exclusivas de sua função balanceOf. Nos tokens ERC20 comuns, a função balanceOf retorna o número de tokens que um endereço possui.
Como os aTokens representam a participação no pool, e não um valor direto, a função balanceOf do aToken retorna a quantidade de tokens subjacentes devidos ao usuário pelo protocolo, para seus depósitos.
pragma solidity ^0.8.13;
function balanceOf(address user)
public
view
override(IncentivizedERC20, IERC20)
returns (uint256)
{
return super.balanceOf(user).rayMul(_pool.getReserveNormalizedIncome(_underlyingAsset));
}
Aqui, a função balanceOf substitui a balanceOf dos contratos aToken herdados. Como resultado, a lógica balanceOf, nessa lógica de exemplo, é executada, em vez da pesquisa de mapeamento regular (herdada) do número de tokens do usuário.
A quantidade de tokens mencionada acima é então multiplicada pelo resultado de getReserveNormalizedIncome, que, por sua vez, executa a seguinte lógica:
pragma solidity ^0.8.13;
function getNormalizedIncome(DataTypes.ReserveData storage reserve)
internal
view
returns (uint256)
{
uint40 timestamp = reserve.lastUpdateTimestamp;
if (timestamp == uint40(block.timestamp)) {
return reserve.liquidityIndex;
}
uint256 cumulated =
MathUtils.calculateLinearInterest(reserve.currentLiquidityRate, timestamp).rayMul(
reserve.liquidityIndex
);
return cumulated;
}
Podemos identificar a derivação aqui:
Se uma atualização dos dados de reserva já tiver ocorrido nesse bloco, retorne o valor
liquidityIndexpara esse mercado, pois já está atualizado.Caso contrário: precisamos ver o que acontece no
calculateLinearInterestpara descobrir o próximo fluxo a ser executado.pragma solidity ^0.8.13; function calculateLinearInterest(uint256 rate, uint40 lastUpdateTimestamp) internal view returns (uint256) { uint256 timeDifference = block.timestamp.sub(uint256(lastUpdateTimestamp)); return (rate.mul(timeDifference) / SECONDS_PER_YEAR).add(WadRayMath.ray()); }
O currentLiquidityRate e o lastUpdateTimestamp do objeto ReserveData do mercado passaram, para essa função, e o resultado será:
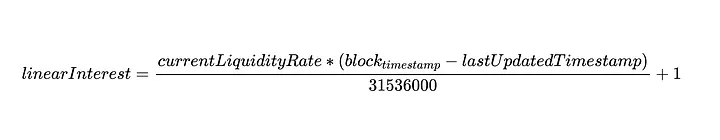
Vamos decompor os componentes dessa equação para entender melhor a essência do valor linearInterest:
- currentLiquidityRate: Pense nisso como o APY (rendimento percentual anual) do mercado em que estamos operando.
- block_{timestamp} - lastUpdatedTimestamp: tempo decorrido desde a última atualização.
Nota: como pegamos a segunda ramificação no getNormalizedIncome, é garantido que esse valor seja positivo nesse ponto!
Portanto, podemos pensar nesse mecanismo de acúmulo de juros como um mecanismo simples de composição de juros, que é composto a cada bloco. Agora que estabelecemos o valor dos juros a serem acumulados para o nosso usuário, basta multiplicar esse valor pelo índice de liquidez para obter a renda normalizada do usuário, multiplicada na função balanceOf:
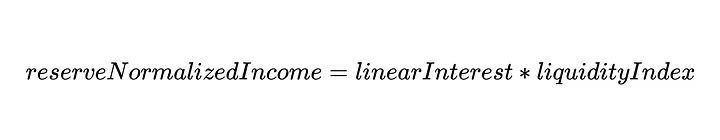
Agora entendemos a lógica por trás dos aTokens, mas ainda precisamos resolver o mistério de como o liquidityIndex funciona.
No exemplo abaixo, o índice de liquidez pode ser definido como os juros acumulados pela reserva durante algum período de tempo:
pragma solidity ^0.8.13;
function _updateIndexes(
DataTypes.ReserveData storage reserve,
uint256 scaledVariableDebt,
uint256 liquidityIndex,
uint256 variableBorrowIndex,
uint40 timestamp
) internal returns (uint256, uint256) {
uint256 currentLiquidityRate = reserve.currentLiquidityRate;
uint256 newLiquidityIndex = liquidityIndex;
uint256 newVariableBorrowIndex = variableBorrowIndex;
if (currentLiquidityRate > 0) {
uint256 cumulatedLiquidityInterest =
MathUtils.calculateLinearInterest(currentLiquidityRate, timestamp);
newLiquidityIndex = cumulatedLiquidityInterest.rayMul(liquidityIndex);
require(newLiquidityIndex <= type(uint128).max, Errors.RL_LIQUIDITY_INDEX_OVERFLOW);
reserve.liquidityIndex = uint128(newLiquidityIndex);
if (scaledVariableDebt != 0) {
uint256 cumulatedVariableBorrowInterest =
MathUtils.calculateCompoundedInterest(reserve.currentVariableBorrowRate, timestamp);
newVariableBorrowIndex = cumulatedVariableBorrowInterest.rayMul(variableBorrowIndex);
require(
newVariableBorrowIndex <= type(uint128).max,
Errors.RL_VARIABLE_BORROW_INDEX_OVERFLOW
);
reserve.variableBorrowIndex = uint128(newVariableBorrowIndex);
}
}
reserve.lastUpdateTimestamp = uint40(block.timestamp);
return (newLiquidityIndex, newVariableBorrowIndex);
}
}
Lembre-se da variável liquidityRate — agora vamos discutir seu uso no cálculo do liquidityIndex. Haverá um acúmulo de juros, somente se o liquidityRate for maior do que 0 — em outras palavras, somente se houver algum APY neste mercado. Faz sentido.
Vamos rever rapidamente, o que o calculateLinearInterest realmente faz:
pragma solidity ^0.8.13;
function calculateLinearInterest(uint256 rate, uint40 lastUpdateTimestamp)
internal
view
returns (uint256)
{
uint256 timeDifference = block.timestamp.sub(uint256(lastUpdateTimestamp));
return (rate.mul(timeDifference) / SECONDS_PER_YEAR).add(WadRayMath.ray());
}
A lógica acima se traduz na seguinte equação:
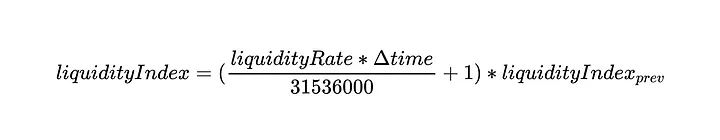
Como podemos ver no contrato DefaultReserveInterestRateStrategy.sol, o liquidityRate é definido por:
pragma solidity ^0.8.13;
function calculateInterestRates(
address _reserve,
uint256 _availableLiquidity,
uint256 _totalBorrowsStable,
uint256 _totalBorrowsVariable,
uint256 _averageStableBorrowRate
)
external
view
returns (
uint256 currentLiquidityRate,
uint256 currentStableBorrowRate,
uint256 currentVariableBorrowRate
)
{
uint256 utilizationRate = (totalBorrows == 0 && _availableLiquidity == 0)
? 0
: totalBorrows.rayDiv(_availableLiquidity.add(totalBorrows));
// ...
currentLiquidityRate = getOverallBorrowRateInternal(
_totalBorrowsStable,
_totalBorrowsVariable,
currentVariableBorrowRate,
_averageStableBorrowRate
)
.rayMul(utilizationRate);
}
Então, ela pode ser escrita assim:

O overallBorrowRate é, por sua vez, definido aqui:
pragma solidity ^0.8.13;
function getOverallBorrowRateInternal(
uint256 _totalBorrowsStable,
uint256 _totalBorrowsVariable,
uint256 _currentVariableBorrowRate,
uint256 _currentAverageStableBorrowRate
) internal pure returns (uint256) {
uint256 totalBorrows = _totalBorrowsStable.add(_totalBorrowsVariable);
if (totalBorrows == 0) return 0;
uint256 weightedVariableRate = _totalBorrowsVariable.wadToRay().rayMul(
_currentVariableBorrowRate
);
uint256 weightedStableRate = _totalBorrowsStable.wadToRay().rayMul(
_currentAverageStableBorrowRate
);
uint256 overallBorrowRate = weightedVariableRate.add(weightedStableRate).rayDiv(
totalBorrows.wadToRay()
);
return overallBorrowRate;
}
}
E podemos escrever isso da seguinte forma:

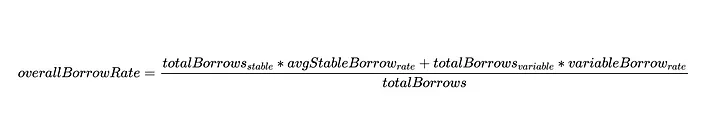
E o utilizationRate pode ser definido como:
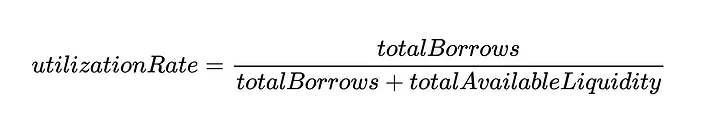
Ao definir o utilizationRate é mais fácil pensar na razão entre a quantidade de liquidez na reserva (atualmente emprestada) e a liquidez total no mercado, que pode ser simplificada como:
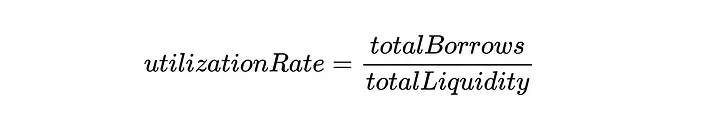
Agora podemos usar essas duas definições para escrever a equação da taxa de liquidez:
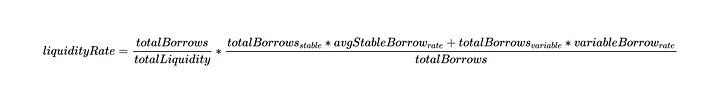
Como o totalBorrows está tanto no numerador quanto no denominador, podemos escrever:
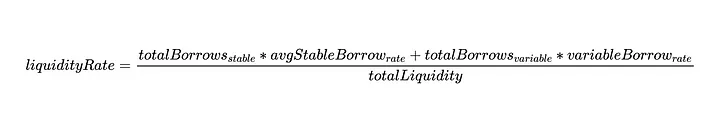
Por enquanto, isso é o suficiente para desenvolver a equação da liquidityRate. Voltaremos a essa definição mais adiante.
cToken: “Share Token” do Compound
Vamos passar para o nosso próximo exemplo de protocolo de empréstimo, o Compound.
O Compound usa um "share token" chamado cToken para lidar com empréstimos e concessões de empréstimos. Esse token faz a contabilidade de todos os ativos disponíveis aos usuários para empréstimos e concessões de empréstimos no protocolo Compound.
Semelhante ao que discutimos no AAVE V2, os "share tokens" do Compound são cunhados e usados para resgatar ativos subjacentes.
O Compound usa uma taxa de câmbio, semelhante ao índice de liquidez da AAVE V2, para decidir quantos cTokens devem ser cunhados. Essa taxa de câmbio é uma função de:
pragma solidity ^0.8.13;
function exchangeRateStoredInternal() internal view returns (MathError, uint) {
uint _totalSupply = totalSupply;
if (_totalSupply == 0) {
return (MathError.NO_ERROR, initialExchangeRateMantissa);
} else {
uint totalCash = getCashPrior();
uint cashPlusBorrowsMinusReserves;
Exp memory exchangeRate;
MathError mathErr;
(mathErr, cashPlusBorrowsMinusReserves) = addThenSubUInt(totalCash, totalBorrows, totalReserves);
if (mathErr != MathError.NO_ERROR) {
return (mathErr, 0);
}
(mathErr, exchangeRate) = getExp(cashPlusBorrowsMinusReserves, _totalSupply);
if (mathErr != MathError.NO_ERROR) {
return (mathErr, 0);
}
return (MathError.NO_ERROR, exchangeRate.mantissa);
}
}
Vamos explicar os principais termos aqui:
totalCash: A quantidade de tokens ERC20 subjacentes pertencentes à conta cToken.totalBorrows: A quantidade de tokens subjacentes ERC20 emprestados a tomadores de empréstimos fora do mercado.totalReserves: Uma quantidade de tokens ERC20 subjacentes reservados para serem retirados ou transferidos por meio de governança.totalSupply: A função ERC20 que retorna o fornecimento total de cTokens.
Nesse contexto, podemos escrever a equação da taxa de câmbio do Compound:
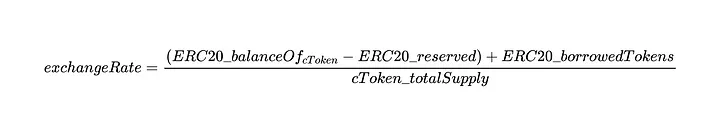
Quando um usuário deposita tokens ERC20, a taxa de câmbio determina quantos cTokens serão cunhados em troca de … eTokens:
pragma solidity ^0.8.13;
function deposit(uint subAccountId, uint amount) external nonReentrant {
(address underlying, AssetStorage storage assetStorage, address proxyAddr, address msgSender) = CALLER();
address account = getSubAccount(msgSender, subAccountId);
updateAverageLiquidity(account);
emit RequestDeposit(account, amount);
AssetCache memory assetCache = loadAssetCache(underlying, assetStorage);
if (amount == type(uint).max) {
amount = callBalanceOf(assetCache, msgSender);
}
amount = decodeExternalAmount(assetCache, amount);
uint amountTransferred = pullTokens(assetCache, msgSender, amount);
uint amountInternal;
unchecked {
assetCache.poolSize -= amountTransferred;
amountInternal = underlyingAmountToBalance(assetCache, amountTransferred);
assetCache.poolSize += amountTransferred;
}
increaseBalance(assetStorage, assetCache, proxyAddr, account, amountInternal);
if (assetStorage.users[account].owed != 0) checkLiquidity(account);
logAssetStatus(assetCache);
}
E a quantidade de cTokens a serem cunhados é definida pela seguinte equação:
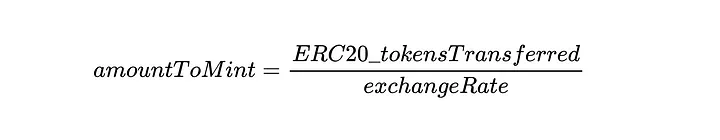
eToken: “Share Token” de Euler
Para solidificar ainda mais a semelhança entre esses protocolos, vamos detalhar outro protocolo de empréstimo, o Euler, e examinar como ele lida com empréstimos e concessões de empréstimos.
No exemplo abaixo, a função deposit permite que os usuários depositem tokens ERC20 em troca de… eTokens.
pragma solidity ^0.8.13;
function computeExchangeRate(AssetCache memory assetCache) private pure returns (uint) {
uint totalAssets = assetCache.poolSize + (assetCache.totalBorrows / INTERNAL_DEBT_PRECISION);
if (totalAssets == 0 || assetCache.totalBalances == 0) return 1e18;
return totalAssets * 1e18 / assetCache.totalBalances;
}
function underlyingAmountToBalance(AssetCache memory assetCache, uint amount) internal pure returns (uint) {
uint exchangeRate = computeExchangeRate(assetCache);
return amount * 1e18 / exchangeRate;
}
Como podemos ver, o internalAmount é a quantidade de eTokens cunhados para essa transferência.
pragma solidity ^0.8.13;
function computeExchangeRate(AssetCache memory assetCache) private pure returns (uint) {
uint totalAssets = assetCache.poolSize + (assetCache.totalBorrows / INTERNAL_DEBT_PRECISION);
if (totalAssets == 0 || assetCache.totalBalances == 0) return 1e18;
return totalAssets * 1e18 / assetCache.totalBalances;
}
function underlyingAmountToBalance(AssetCache memory assetCache, uint amount) internal pure returns (uint) {
uint exchangeRate = computeExchangeRate(assetCache);
return amount * 1e18 / exchangeRate;
}
Mais um overlap (sobreposição) direto com o Compound: o nome e a função do exchangeRate.
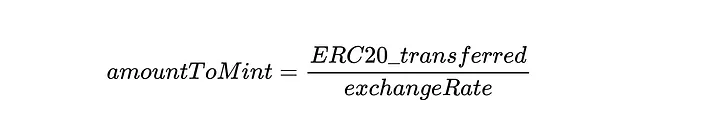
Vamos explicar os principais parâmetros que são usados para calcular a taxa de câmbio:
poolSize: O resultado de chamar balanceOf(address) com o endereço do contrato de pool, no contrato ERC20 do ativo subjacente.totalBorrows: O valor total de ERC20 emprestado e não presente, no momento, no pool.totalBalances: Os saldos totais de todos os detentores de eToken.
Então, a equação será:
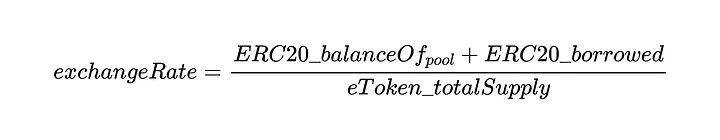
Generalização
Para recapitular, abordamos três protocolos de empréstimo:
AAVE V2
Compound
Euler
Examinamos a cunhagem de "Share Tokens" e como eles são trocados por ativos depositados por meio de pools de empréstimos. As três equações que apresentamos para mostrar como esses processos funcionam podem ser simplificadas em uma única equação:
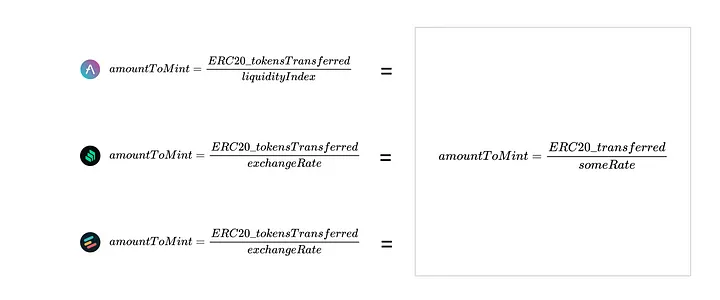
Lembre-se de que as taxas de câmbio podem ser definidas da forma que o protocolo definir. Essas taxas arbitrárias podem aumentar a quantidade de tokens cunhados se $<$1 e diminuir a quantidade se $>$1.
Tanto na AAVE V2 quanto no Compound, vimos alguma semelhança em como a variável $someRate$ é definida. No Compound, o someRate é:

E para a AAVE V2 o someRate é definido assim:
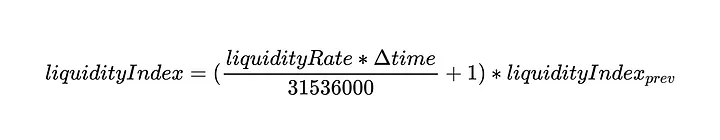
Com a taxa de liquidez definida como:
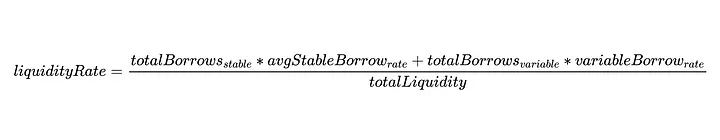
Embora não possamos generalizar a taxa para cada protocolo, tanto para o AAVE2 quanto para o Compound, sabemos que a taxa é uma função da liquidez total no mercado. Voltando às nossas equações, dado que o totalLiquidity é a quantidade total de tokens subjacentes ERC20 em um mercado, o numerador na expressão do exchangeRate e o denominador do liquidityRate são funcionalmente os mesmos.
Apenas para recapitular: esses protocolos são praticamente os mesmos. Embora às vezes eles possam usar nomenclaturas diferentes, quando decompostos em equações, cada componente tem uma finalidade semelhante em sua implementação. Convidamos os leitores a escolher um protocolo de empréstimo aleatório e verificar se a generalização que discutimos aqui também se aplica a ele. Se for o caso, fique à vontade para nos informar! 🙂
Agradecimentos ao Sam Ragsdale e os membros do time smlXL que forneceram orientações e feedback para esta postagem.
Responda a esta postagem se tiver alguma dúvida, e Tweet at us se você tiver um tópico que gostaria que abordássemos.
Esse artigo foi escrito por Tal e traduzido por Fátima Lima. O original pode ser lido aqui.

