Este artigo apresenta um algoritmo para a distribuição descentralizada eficiente de recompensas entre os participantes de pool com uma taxa de recompensa variável com base na quantidade de tokens de recompensa a serem distribuídos, que atinge a complexidade de tempo O(1). O algoritmo proposto é particularmente útil para projetos de mineração de liquidez na blockchain Ethereum, onde as restrições de gas tornam impraticável a distribuição de recompensas a cada bloco. O artigo demonstra a eficiência e a escalabilidade do algoritmo proposto e apresenta alguns casos de uso em potencial para sua aplicação em contratos inteligentes.
N.T. O(1) complexity significa que o tempo de execução de um algoritmo não depende do número de inputs e é constante.
1. Introdução
As finanças descentralizadas (DeFi) surgiram como um dos setores mais empolgantes e de rápido crescimento no ecossistema de blockchains. Os protocolos DeFi permitem que os usuários realizem transações financeiras, como empréstimos, financiamentos, negociações e staking, de forma descentralizada e sem confiança. Um dos principais recursos dos protocolos DeFi é a capacidade de distribuir recompensas aos participantes em troca de sua contribuição para a rede, como o fornecimento de liquidez, o staking de tokens [1] ou o desempenho de funções de governança [2].
A distribuição de recompensas é um componente fundamental de muitos protocolos DeFi e sua implementação eficiente e justa é essencial para a sustentabilidade e o crescimento desses projetos. No entanto, projetar um algoritmo de distribuição de recompensas ideal não é uma tarefa simples e vários desafios precisam ser enfrentados, incluindo restrições de gas, taxas de recompensa variáveis e a necessidade de escalar para um grande número de participantes.
Vários algoritmos foram propostos para enfrentar esses desafios, mas a maioria deles sofre de limitações significativas. Por exemplo, o Scalable Reward Distribution on the Ethereum Blockchain (Batog, Boca & Johnson, 2018) [3] só é adequado para uma distribuição muito bem otimizada (por exemplo, cada bloco), o que não é viável para a maioria dos projetos devido a restrições de gas. O contrato StakingRewards [4] da Synthetix e o MasterChef [5] da Sushi pressupõem intervalo de tempo ou taxa de recompensa constantes, o que não funciona para projetos de mineração de liquidez com recompensas de tokens variáveis.
Neste artigo, propomos um novo algoritmo para distribuição descentralizada de recompensas em contratos inteligentes que supera essas limitações e mantém a complexidade de tempo O(1). Nosso algoritmo pode lidar com taxas de recompensa variáveis com base na quantidade de tokens de recompensa necessários para serem distribuídos e é particularmente útil para projetos de mineração de liquidez que têm longos intervalos de tempo entre as distribuições de tokens. Também discutimos a implementação do nosso algoritmo como um contrato inteligente da Ethereum, comparamos nossa abordagem com outros algoritmos existentes e destacamos suas vantagens.
2. Trabalhos relacionados
A distribuição de recompensas é um problema bem estudado no contexto de sistemas baseados em blockchain e vários algoritmos foram propostos para resolvê-lo. Nesta seção, apresentamos uma visão geral dos trabalhos relacionados à distribuição de recompensas em contratos inteligentes.
2.1. Algoritmos de taxa de recompensa constante
Vários protocolos DeFi usam algoritmos de taxa de recompensa constante para a distribuição de recompensas. Por exemplo, o contrato MasterChef [5] da Sushiswap pressupõe uma taxa de recompensa constante, o que significa que a taxa de recompensas em tokens é fixa e não muda com o tempo. Embora os algoritmos de taxa de recompensa constante sejam simples e fáceis de serem implementados, eles não funcionam bem para projetos de mineração de liquidez com recompensas de token variáveis.
2.2. Algoritmos baseados no tempo
Outra classe de algoritmos de distribuição de prêmios é a baseada em intervalos de tempo. Esses algoritmos distribuem recompensas em intervalos de tempo fixos, como diariamente ou semanalmente. No entanto, os algoritmos baseados em tempo sofrem de várias limitações, como a incapacidade de lidar com intervalos de tempo variáveis, a necessidade de intervenção manual para ajustar a frequência de distribuição e a possibilidade de acúmulo e perda de recompensas devidos a intervalos perdidos. Como exemplo, o algoritmo StakingRewards [4] da Synthetix pertence a essa categoria.
2.3. Algoritmos Off-Chain
Os algoritmos de distribuição off-chain, como os que usam árvores de Merkle [6][7], tornaram-se populares para a distribuição eficiente de recompensas. Eles armazenam informações de distribuição de recompensas off-chain e usam provas criptográficas para verificação, reduzindo os custos de gas e aumentando a segurança. No entanto, elas podem exigir infraestrutura e coordenação entre os componentes off-chain e on-chain adicionais. Além disso, se o armazenamento off-chain e o cálculo de tal algoritmo forem controlados por uma única entidade, por exemplo, um servidor centralizado, essa solução seria centralizada.
2.4. Algoritmos baseados em blocos
Alguns algoritmos de distribuição de recompensas baseiam-se na suposição de que as recompensas são distribuídas toda vez que um novo bloco é adicionado à blockchain. Embora os algoritmos baseados em blocos possam proporcionar uma distribuição de recompensas escalável e ideal, eles sofrem com as restrições de gas e não são uma solução prática para a maioria dos projetos DeFi. Um exemplo de tal algoritmo é o Scalable Reward Distribution on the Ethereum Blockchain (Batog, Boca & Johnson, 2018) [3]. Esse algoritmo não rastreia o momento em que os participantes entram no pool e, portanto, não funciona bem com longos intervalos de distribuição. Os participantes poderiam entrar no pool pouco antes da distribuição de prêmios e receber prêmios que não ganharam.
2.5. Nossa Solução
Embora vários algoritmos tenham sido desenvolvidos para lidar com a distribuição de recompensas em contratos inteligentes, a maioria deles sofre de limitações significativas. Nosso algoritmo proposto supera essas limitações e atinge a complexidade de tempo O(1), o que o torna uma solução eficiente e escalável para a distribuição de recompensas em protocolos DeFi.
3. Algoritmo de Distribuição de Recompensa
Começaremos descrevendo os principais componentes do algoritmo:
- Deposit(amount): essa função permite que os participantes depositem seus tokens no pool, atualizando sua participação e o valor total de tokens depositados.
- Withdraw(amount): essa função permite que os participantes retirem tokens de sua participação, atualizando sua participação e a quantidade total de tokens restantes no pool de distribuição.
- CollectReward(amount): essa função permite que os participantes recolham sua recompensa do pool, que é calculada com base em sua participação, no tempo em que seus tokens permaneceram no pool e nas distribuições das quais participaram.
- Distribute(reward): essa função distribui os prêmios entre os participantes. O contrato utiliza um sistema pullbased para manter a complexidade de tempo constante. Os participantes devem chamar posteriormente a CollectReward para receber suas recompensas.
Para evitar o problema descrito na seção 2.4, o algoritmo também deve rastrear os horários em que os participantes fizeram depósitos. Vários desafios tornam o cálculo dos prêmios que um participante deve receber uma tarefa nada simples:
- Um participante pode fazer um número ilimitado de depósitos e saques em diferentes blocos e com valores variados.
- Um número infinito de distribuições com valores de recompensa variáveis pode ocorrer em diferentes intervalos de tempo.
3.1. Recompensa do Participante Após uma Única Distribuição
Para determinar a recompensa de um participante após uma única distribuição, devemos considerar a ordem cronológica de todos os eventos de depósito, retirada e distribuição. Sejam T₁, T₂, ..., Tₙ a soma de todas as apostas ativas em cada bloco t₁, t₂, ..., tₙ em que ocorreu um depósito ou retirada, onde n é o bloco em que a recompensa é distribuída. Um participante i teria stakeᵢ,₁, stakeᵢ,₂, ..., stakeᵢ,ₙ em cada um desses blocos, dependendo de seus depósitos e retiradas.
Vamos atribuir nomes às seguintes expressões:
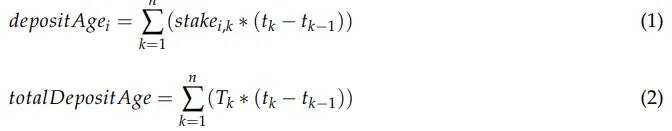
O participant i receberá a recompensa:
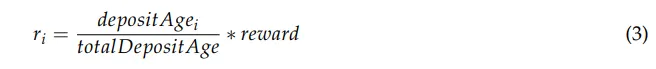
Podemos acumular totalDepositAge em cada depósito e retirada, possibilitando o cálculo de (2) em tempo constante na coleção de recompensas de i. Como a participação de i é constante durante o intervalo em que nenhum depósito ou saque foi feito por ele, podemos reescrever (1) como:
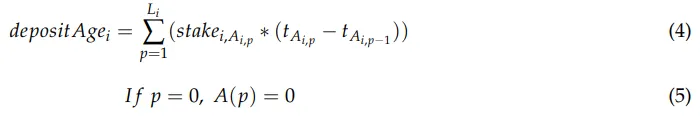
Aqui, Lᵢ representa o número de depósitos e saques feitos pelo participante i e Aᵢ,ₚ representa o bloco i feito na ação p. Também podemos acumular _depositAge_ᵢ para os participantes em seus depósitos e saques, o que nos permite calcular (4) em tempo constante. Portanto, também podemos calcular rᵢ em tempo constante.
3.2. Recompensa do Participante Após Múltiplas Distribuições
Consideremos o caso em que o participante i deposita sua aposta antes da distribuição d e a mantém para múltiplas distribuições d, d + 1, ..., D. Sua recompensa R seria:
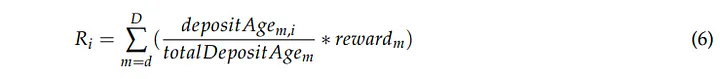
Após a primeira distribuição d, o participante i receberá uma recompensa de (3). Se m > d, sua participação permaneceria constante:

Podemos armazenar a última distribuição D em cada nova distribuição e armazenar a próxima distribuição d para cada participante i em cada uma de suas ações, possibilitando o cálculo de rewardAgePerDepositAge_D_−rewardAgePerDepositAged num tempo constante.
Também podemos calcular rd,ᵢ num tempo constante, armazenando o rewardd/totalDepositAged para cada distribuição d e multiplicar pelo _depositAge_ᵢ na coleção de recompensas de i. Portanto, também é possível calcular Rᵢ num tempo constante.
3.3. Outros Casos
Qualquer outro caso pode ser modelado adicionando várias expressões (11) juntas e substituindo d pela próxima distribuição após a última ação de i. O algoritmo permanece num tempo constante porque podemos acumular as recompensas de i em cada uma de suas ações.


4. Notas
- As funções Withdraw e CollectReward podem ser mescladas em uma única função para maior simplicidade e eficiência.

O algoritmo atual não oferece suporte a recompensas compostas, mas há potencial para desenvolvimento futuro.
Os participantes que investiram em seus tokens durante um determinado intervalo de distribuição receberão recompensas, mesmo que não tenham uma participação ativa no momento da distribuição da recompensa. Por exemplo, se eles retiraram seus tokens antes da distribuição, ainda assim receberão suas recompensas após a distribuição. Esse é um comportamento esperado porque o algoritmo descrito tem como objetivo oferecer uma distribuição justa de prêmios a todos os participantes.
O algoritmo foi projetado para ser livre de loop, garantindo uma distribuição de recompensas eficiente e escalável.
5. Informação do Autor
Esse algoritmo foi desenvolvido para o protocolo de mineração de liquidez Uno.Farm [8]. O Uno.Farm [8] é um exemplo de implementação bem-sucedida do algoritmo descrito neste documento e o utiliza para distribuir recompensas de pools de staking de terceiros entre os participantes.
6. Conclusão
Este artigo propõe um novo algoritmo para distribuição eficiente e descentralizada de recompensas em contratos inteligentes. O algoritmo proposto supera várias limitações dos algoritmos existentes ao lidar com taxas de recompensa variáveis com base na quantidade de tokens de recompensa necessários para serem distribuídos, mantendo a complexidade de tempo O(1). No contexto dos protocolos DeFi, a distribuição eficiente e justa de recompensas é fundamental para sua sustentabilidade e crescimento. O algoritmo proposto oferece uma solução promissora para enfrentar os desafios das restrições de gas, taxas de recompensa variáveis e escalabilidade para um grande número de participantes. Ele pode contribuir para o desenvolvimento de um ecossistema DeFi mais robusto e eficiente.
Referências (em inglês)
[1] Vogelsteller, F. & Buterin, V. (2015). ERC: Token standard 20 (ERC: Token padrão 20). Acessado em https://github.com/ethereum/EIPs/blob/master/EIPS/eip-20.md.
[2] Buterin, V. (2014). A next-generation smart contract and decentralized application platform. Ethereum white paper (Um contrato inteligente de última geração e plataforma de aplicativos descentralizada. Artigo técnico da Ethereum). Acessado em https://ethereum.org/en/whitepaper/.
[3] Batog, B., Boca, L., & Johnson, N. (2018) Scalable reward distribution on the Ethereum blockchain (Distribuição de recompensas escalável na blockchain Ethereum). DappCon, Berlin, Germany, Aug. 2018.
[4] Synthetix. (2021). StakingRewards Contract (Contrato StakingRewards). Acessado em https://github.com/Synthetixio/synthetix/blob/develop/contracts/StakingRewards.sol.
[5] SushiSwap. (2021). MasterChef Contract (Contrato MasterChef). Acessado em https://github.com/sushiswap/sushiswap/blob/master/protocols/masterchef/contracts/MasterChefV2.sol.
[6] Merkle, R. C. (1988). A Digital Signature Based on a Conventional Encryption Function. Advances in Cryptology (Assinatura digital baseada em uma função de criptografia convencional. Avanços em Criptologia)— CRYPTO ’87. Lecture Notes in Computer Science (Notas de aula em Ciências da Computação). Vol. 293. pp. 369–378.
[7] Uniswap. (2020). MerkleDistributor contract (Contrato MerkleDistributor). Acessado em https://github.com/Uniswap/merkle-distributor/blob/master/contracts/MerkleDistributor.sol.
[8] Uno.Farm. Yield farming aggregator protocol (Protocolo agregador de mineração de liquidez). https://uno.farm/.
Agradecimentos especiais a Anton Dementyev.
Esse artigo foi escrito por Ivan Menshchikov (Juglipaff) e Roman Vinogradov (sapph1re) e traduzido por Fátima Lima. O original pode ser lido aqui.

