A inteligência artificial tem testemunhado um crescimento monumental na redução da lacuna entre as capacidades dos humanos e das máquinas. Pesquisadores e entusiastas trabalham em vários aspectos da área para fazer coisas incríveis acontecerem. Uma dessas muitas áreas é o domínio da visão computacional.
O plano para este campo é permitir que as máquinas vejam o mundo como os humanos, percebam-no de maneira semelhante e até mesmo usem o conhecimento para uma infinidade de tarefas, como reconhecimento de imagens e vídeos, análise e classificação de imagens, recriação de mídia, sistemas de recomendação, processamento de linguagem natural, etc. Os avanços em visão computacional com aprendizado profundo foram construídos e aperfeiçoados com o tempo, principalmente por meio de um algoritmo específico - uma rede neural convolucional.
Pronto para experimentar suas próprias redes neurais convolucionais? Confira o Saturn Cloud para computação gratuita (incluindo GPUs gratuitas).
Introdução
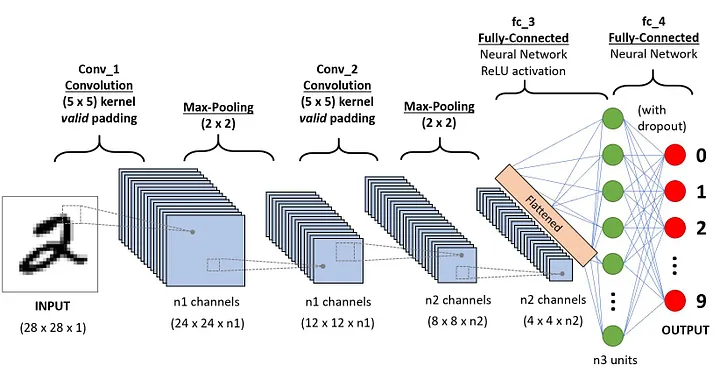
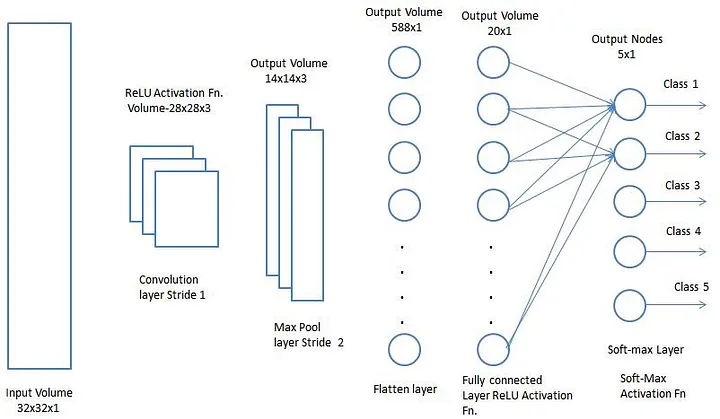
Uma sequência CNN para classificar dígitos manuscritos
Uma Rede Neural Convolucional (ConvNet/CNN) é um algoritmo de aprendizado profundo que pode receber uma imagem de entrada, atribuir importância (pesos e vieses que podem ser aprendidos) a vários aspectos/objetos na imagem e ser capaz de diferenciar um do outro. O pré-processamento necessário em uma ConvNet é muito menor em comparação com outros algoritmos de classificação. Embora nos métodos primitivos os filtros sejam projetados manualmente, com treinamento suficiente, as ConvNets têm a capacidade de aprender esses filtros/características.
A arquitetura de uma ConvNet é análoga à do padrão de conectividade dos neurônios no cérebro humano e foi inspirada na organização do córtex visual. Neurônios individuais respondem a estímulos apenas em uma região restrita do campo visual conhecida como campo receptivo. Um conjunto desses campos se sobrepõe para cobrir toda a área visual.
Por que ConvNets em Vez de Redes Neurais Feed-Forward?
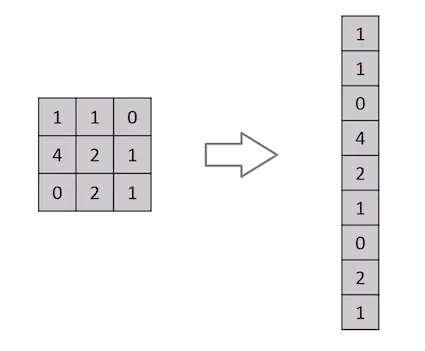
Achatamento de uma matriz de imagem 3x3 em um vetor 9x1
Uma imagem nada mais é do que uma matriz de valores de pixels, certo? Então, por que não simplesmente achatar a imagem (por exemplo, uma matriz de imagem 3x3 em um vetor 9x1) e alimentá-la em um Perceptron multinível para fins de classificação? Uh... na verdade não.
No caso de imagens binárias extremamente básicas, o método pode mostrar uma pontuação de precisão média ao realizar a previsão de classes, mas teria pouca ou nenhuma precisão quando se trata de imagens complexas com dependências de pixel por toda parte.
Uma ConvNet é capaz de captar com sucesso as dependências espaciais e temporais em uma imagem através da aplicação de filtros relevantes. A arquitetura realiza um melhor ajuste ao conjunto de dados de imagens devido à redução no número de parâmetros envolvidos e à reutilização de pesos. Em outras palavras, a rede pode ser treinada para compreender melhor a sofisticação da imagem.
Imagem de Entrada
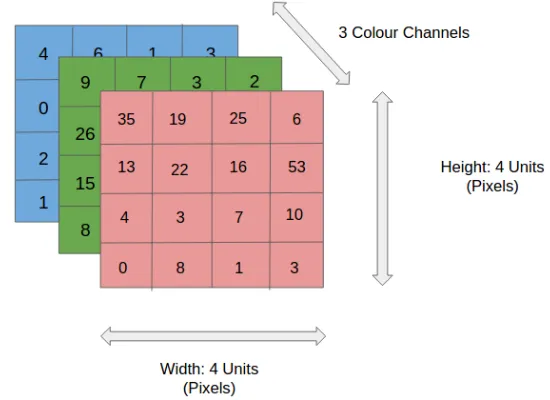
Imagem RGB 4x4x3
Na figura, temos uma imagem RGB separada por seus três planos de cores – vermelho, verde e azul. Existem vários espaços de cores nos quais as imagens existem - tons de cinza, RGB, HSV, CMYK, etc.
Você pode imaginar como as coisas se tornariam computacionalmente intensivas quando as imagens atingissem dimensões, digamos, de 8K (7680×4320). O papel da ConvNet é reduzir as imagens para um formato mais fácil de processar, sem perder características essenciais para obtenção de uma boa previsão. Isso é importante quando pretendemos projetar uma arquitetura que não seja apenas boa em aprender características, mas também seja escalável para conjuntos de dados em massa.
Camada de Convolução – O Kernel
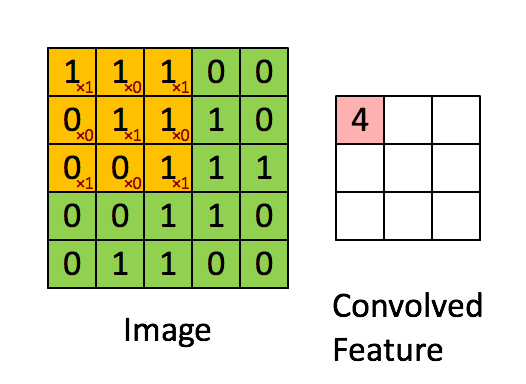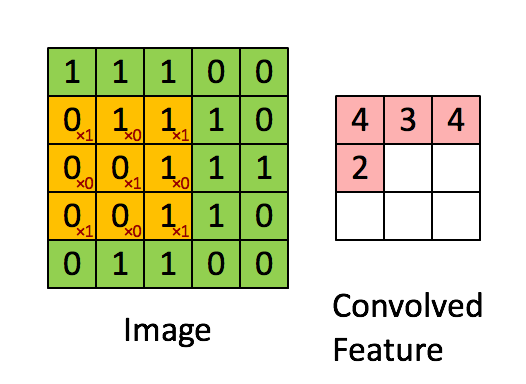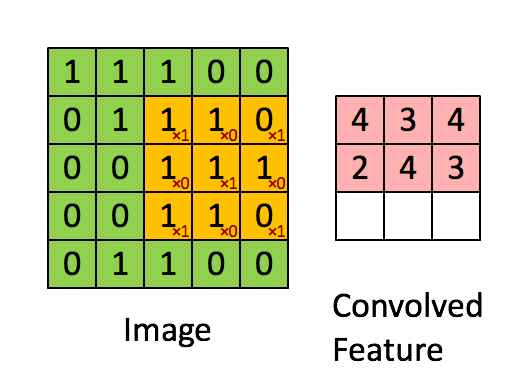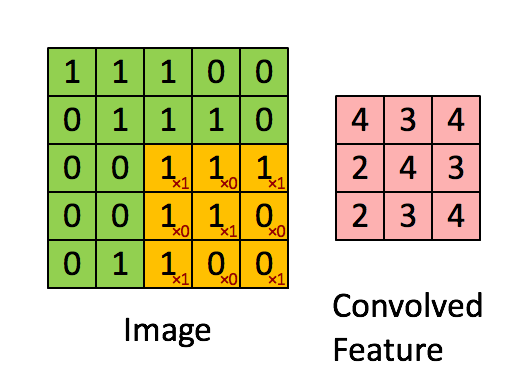
Convoluindo uma imagem 5x5x1 com um kernel 3x3x1 para obter uma característica convolucionada 3x3x1
Dimensões da imagem = 5 (altura) x 5 (largura) x 1 (número de canais, por exemplo, RGB).
Na demonstração acima, a seção verde se assemelha à nossa imagem de entrada 5x5x1, I. O elemento envolvido na operação de convolução na primeira parte de uma camada convolucional é denominado Kernel/Filtro, K, representado na cor amarela. Selecionamos K como uma matriz 3x3x1.
Kernel/Filtro, K =
1 0 1
0 1 0
1 0 1
O Kernel muda 9 vezes devido ao comprimento do deslocamento (Stride Length) = 1 (Non-Strided ou sem deslocamento), sempre realizando uma operação de multiplicação elemento a elemento (Produto Hadamard) entre K e a parte P da imagem sobre a qual o Kernel está pairando.
Movimento do Kernel
O filtro se move para a direita com um determinado valor de deslocamento até analisar toda a largura. Seguindo em frente, ele desce até o início (à esquerda) da imagem com o mesmo valor de deslocamento e repete o processo até que toda a imagem seja percorrida.
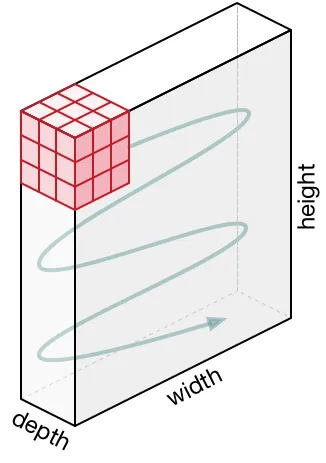
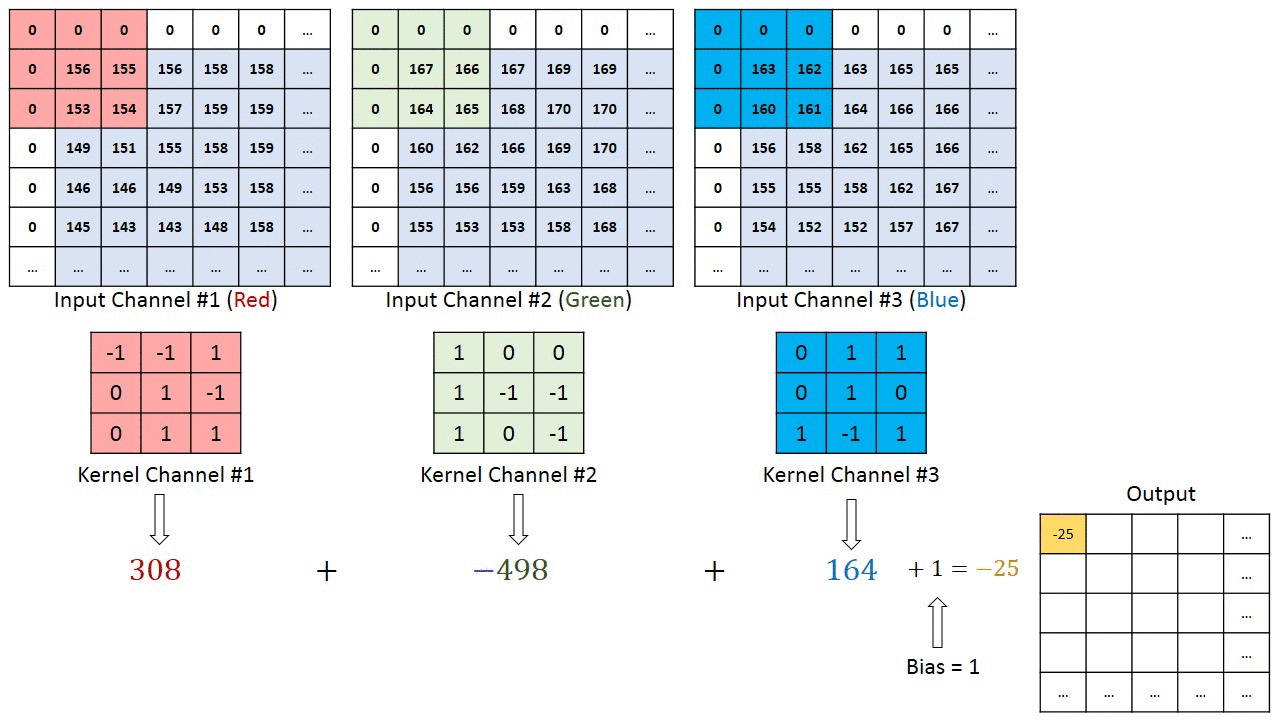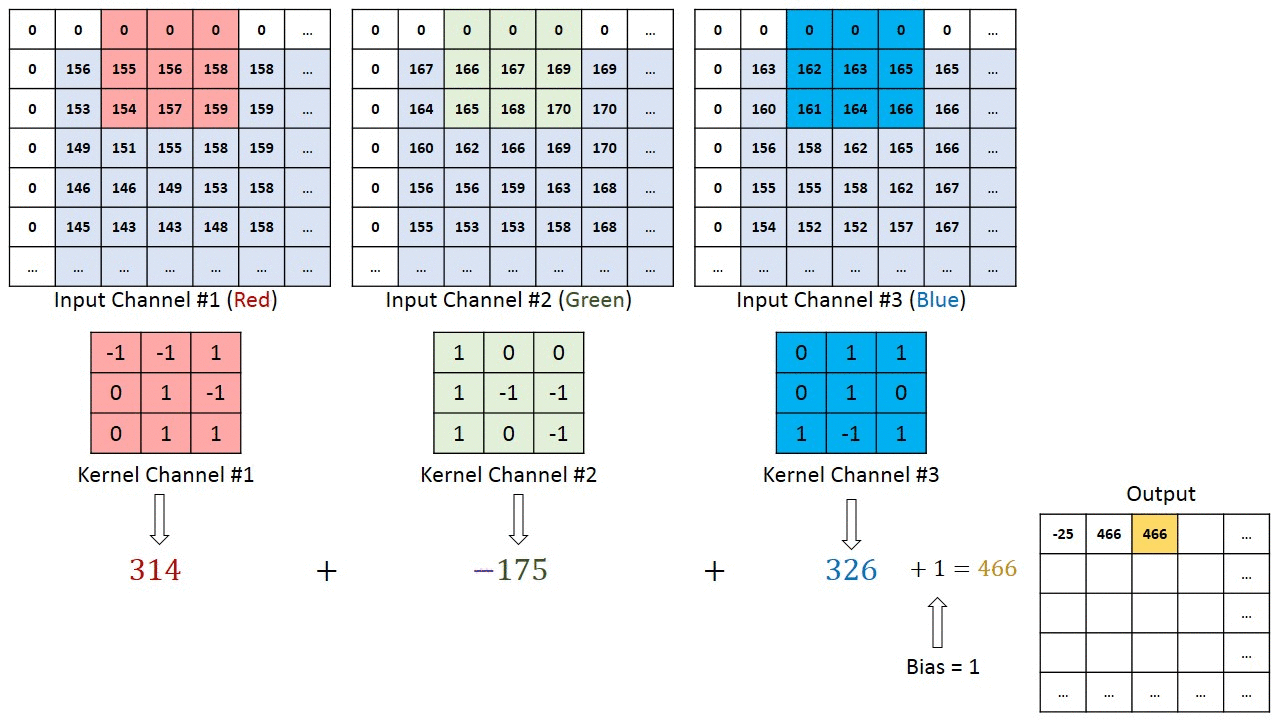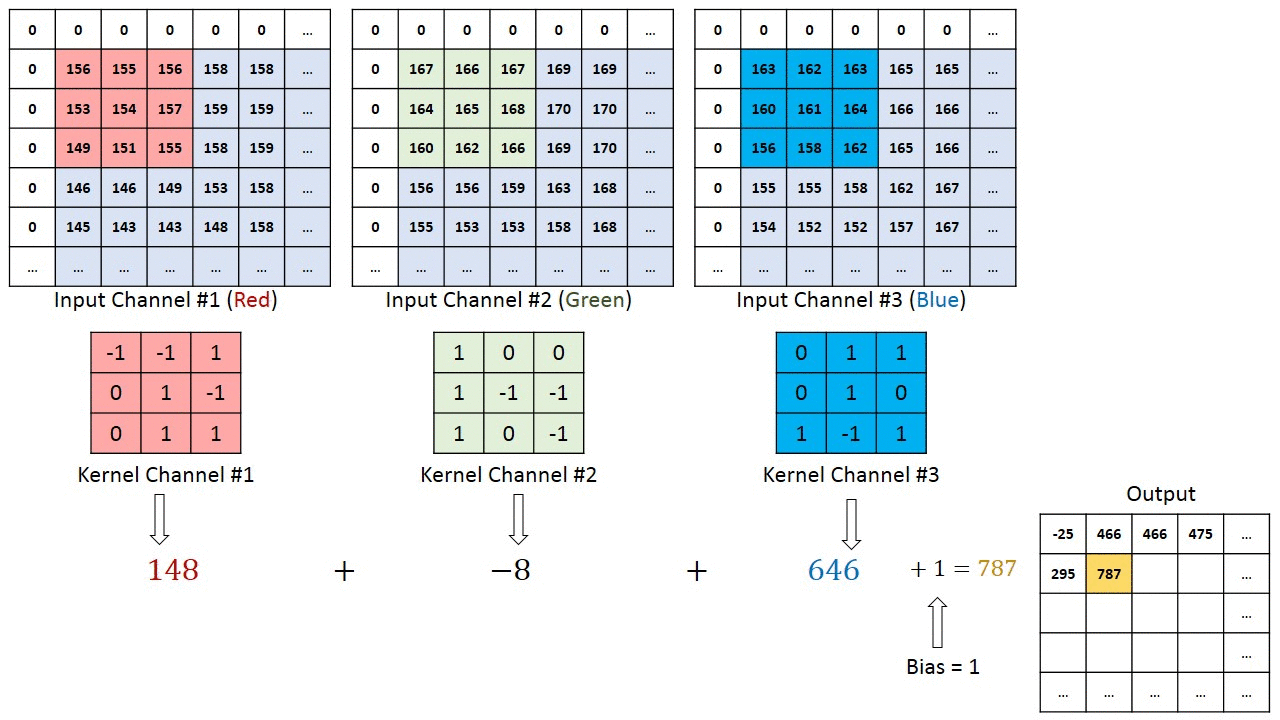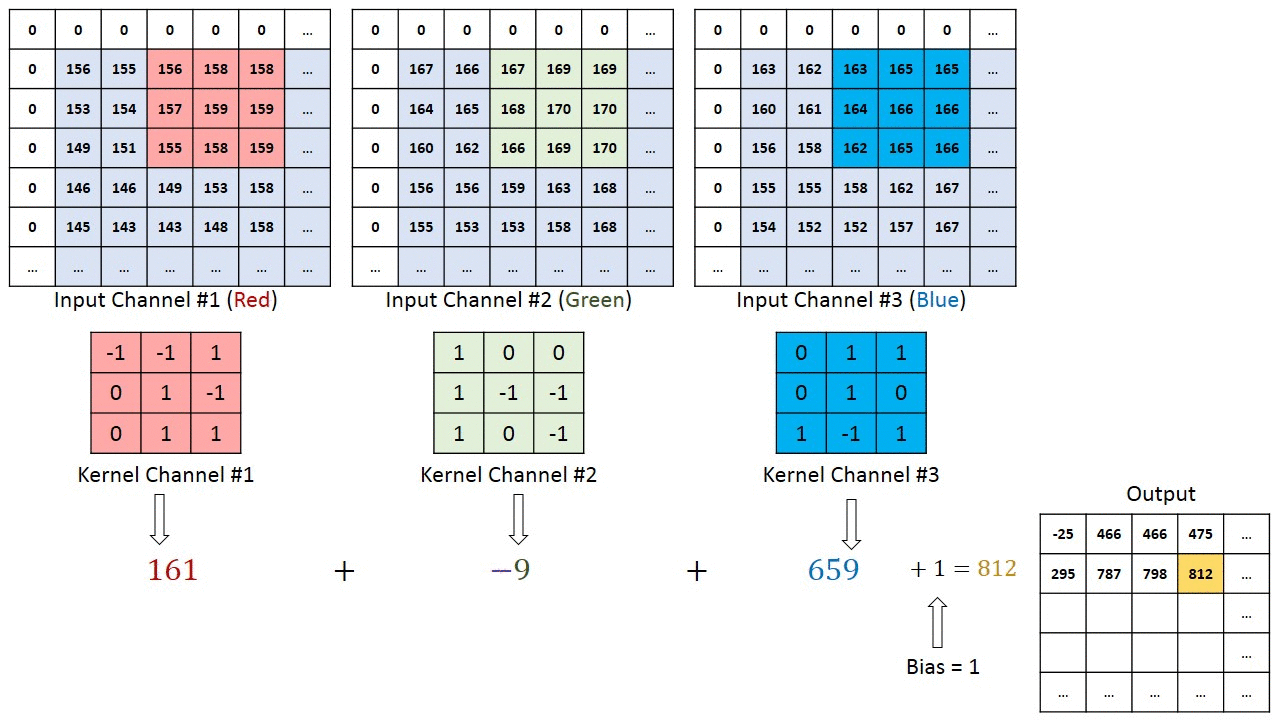
Operação de convolução em uma matriz de imagem MxNx3 com um Kernel 3x3x3
No caso de imagens com múltiplos canais (por exemplo, RGB), o Kernel tem a mesma profundidade da imagem de entrada. A multiplicação da matriz é realizada entre as pilhas Kn e In ([K1, I1]; [K2, I2]; [K3, I3]) e todos os resultados são somados com o viés para nos fornecer uma saída de característica convolucionada de canal de uma profundidade comprimida.
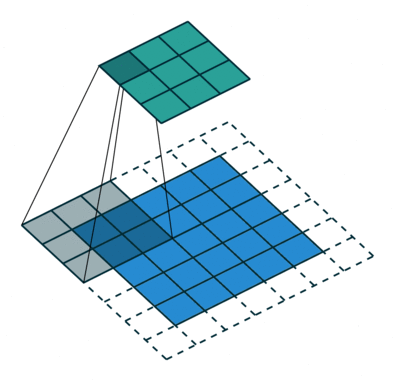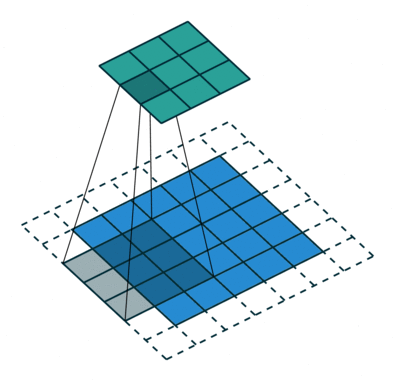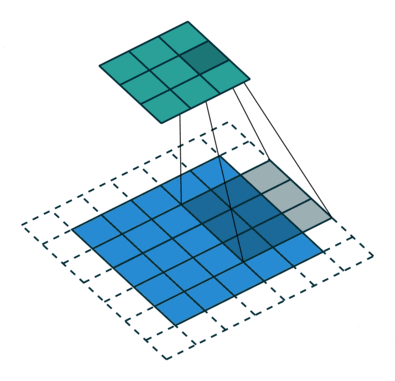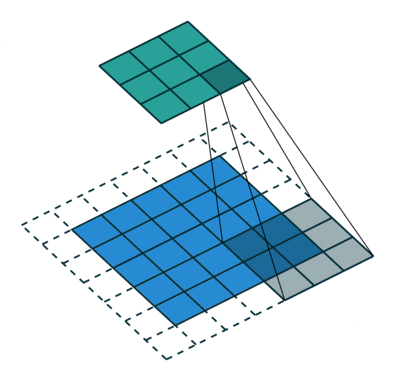
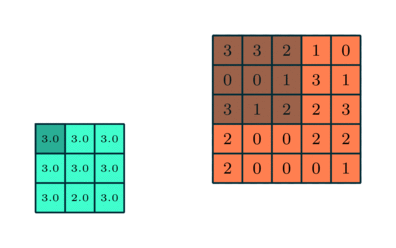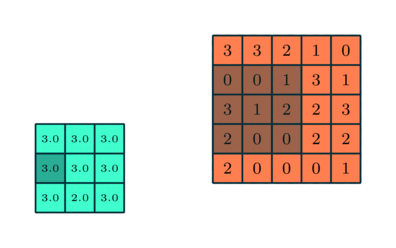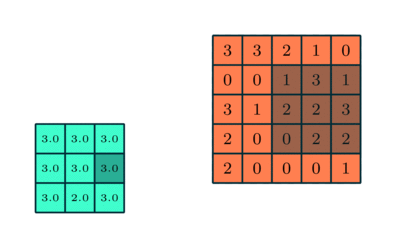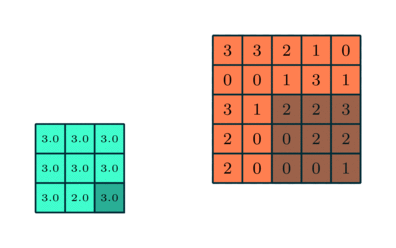
Operação de convolução com comprimento de deslocamento = 2
O objetivo da Operação de Convolução é extrair as características de alto nível, como as bordas, da imagem de entrada. As redes de convolução (ConvNets) não precisam estar limitadas a apenas uma camada convolucional. Convencionalmente, a primeira camada de convolução (ConvLayer) é responsável por captar as características de baixo nível, como bordas, cores, orientação de gradiente, etc. Com camadas adicionadas, a arquitetura também se adapta às características de alto nível, dando-nos uma rede que possui uma compreensão completa de imagens no conjunto de dados, semelhante à que nós teríamos.
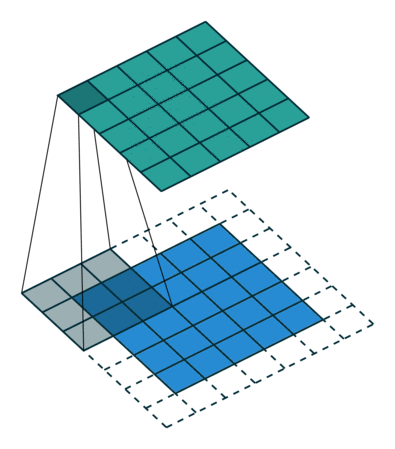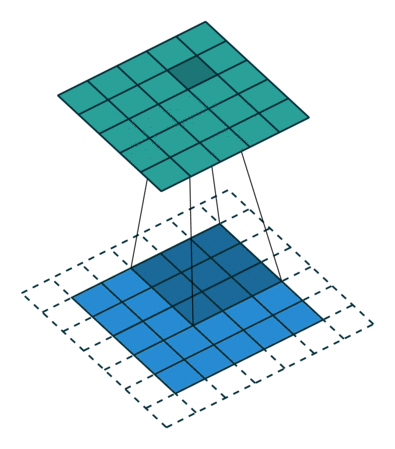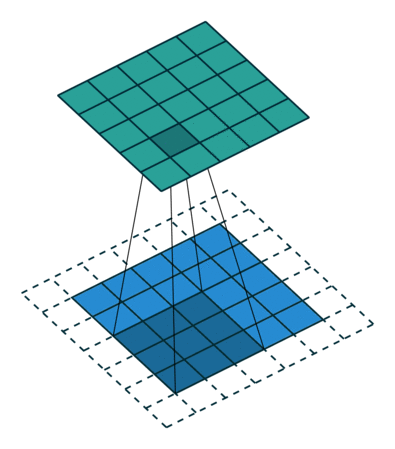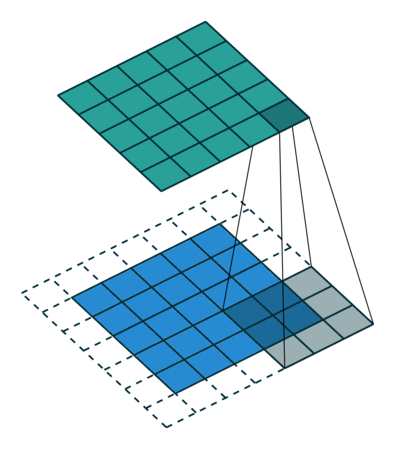
Existem dois tipos de resultados para a operação - um em que a característica convolucionada tem sua dimensionalidade reduzida em comparação com a entrada e outro em que a dimensionalidade é aumentada ou permanece a mesma. Isso é feito aplicando o preenchimento válido (Valid Padding), no caso do primeiro, ou o preenchimento idêntico (Same Padding), no segundo.
Preenchimento IDÊNTICO: a imagem 5x5x1 é preenchida com 0s para criar uma imagem 6x6x1
Quando aumentamos a imagem 5x5x1 em uma imagem 6x6x1 e depois aplicamos o Kernel 3x3x1 sobre ela, descobrimos que a matriz convolucionada tem dimensões 5x5x1. Daí o nome — preenchimento idêntico.
Por outro lado, se realizarmos a mesma operação sem preenchimento, somos apresentados a uma matriz que possui as dimensões do próprio Kernel (3x3x1) — preenchimento válido.
O repositório a seguir contém muitos desses GIFs que podem ajudá-lo a entender melhor como o preenchimento e o comprimento do deslocamento funcionam juntos para obter resultados relevantes às nossas necessidades.
Camada de Pooling (Subamostragem)
Pooling 3x3 sobre característica convolucionada 5x5
Semelhante à camada convolucional, a camada de pooling é responsável por reduzir o tamanho espacial da característica convolucionada. O objetivo é diminuir o poder computacional necessário para processar os dados por meio da redução da dimensionalidade. Além disso, é útil para extrair características dominantes que são invariantes em termos de rotação e posição, mantendo assim o processo de treinamento eficaz do modelo.
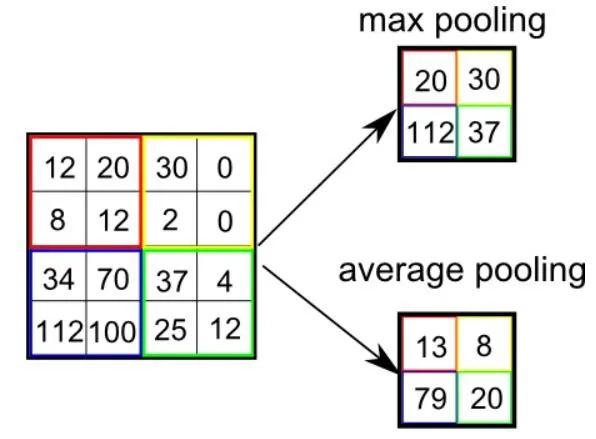
Existem dois tipos de pooling: pooling máximo e pooling médio. O pooling máximo retorna o valor máximo da parte da imagem coberta pelo Kernel. Por outro lado, o pooling médio retorna a média de todos os valores da parte da imagem coberta pelo Kernel.
O pooling máximo também funciona como supressor de ruído. Ele descarta completamente as ativações ruidosas e também realiza a eliminação de ruído junto com redução de dimensionalidade. Por outro lado, o pooling médio simplesmente realiza a redução da dimensionalidade como um mecanismo de supressão de ruído. Portanto, podemos dizer que o pooling máximo tem um desempenho muito melhor do que o pooling médio.
Tipos de Pooling
A camada convolucional e a camada de pooling, juntas, formam a i-ésima camada de uma rede neural convolucional. Dependendo da complexidade das imagens, o número dessas camadas pode ser aumentado para captar ainda mais detalhes de baixo nível, mas a custo de mais poder computacional.
Depois de passar pelo processo descrito acima, habilitamos com sucesso o modelo para compreender as características. Seguindo em frente, vamos nivelar o resultado final e alimentá-lo em uma rede neural regular para fins de classificação.
Classificação — Camada Totalmente Conectada (Camada FC - Fully Connected)
Adicionar uma camada totalmente conectada é uma maneira (geralmente) barata de aprender combinações não lineares das características de alto nível, conforme representado pela saída da camada convolucional. A camada totalmente conectada está aprendendo uma função possivelmente não linear nesse espaço.
Agora que convertemos nossa imagem de entrada em um formato adequado para nosso Perceptron multinível, vamos nivelar a imagem em um vetor coluna. A saída nivelada é alimentada em uma rede neural feed-forward (alimentada para frente) e a retropropagação é aplicada a cada iteração de treinamento. Ao longo de uma série de épocas, o modelo é capaz de distinguir entre características dominantes e certas características de baixo nível nas imagens e classificá-las usando a técnica de classificação Softmax.
Existem várias arquiteturas de CNNs disponíveis que têm sido fundamentais na construção de algoritmos que alimentam e deverão alimentar a IA como um todo no futuro próximo. Algumas delas foram listadas abaixo:
- LeNet
- AlexNet
- VGGNet
- GoogleLeNet
- ResNet
- ZFNet
GitHub Notebook – Reconhecendo dígitos escritos à mão usando conjunto de dados MNIST com TensorFlow
Pronto para experimentar suas próprias redes neurais convolucionais? Confira o Saturn Cloud para computação gratuita (incluindo GPUs gratuitas).
Este artigo foi escrito por Sumit Saha e traduzido por Isabela Curado Nehme. Seu original pode ser lido aqui.









Oldest comments (0)