Série sobre Rede Neural Profunda do Zero em Rust
Após nosso último artigo, precisamos definir uma função de perda para calcular o quão errado nosso modelo está neste momento. Para um problema simples de classificação binária, a função de perda é dada conforme abaixo:
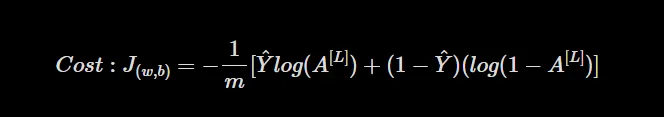
onde,
m ⇾ Número de exemplos de treinamento
Y ⇾ Rótulos de Treinamento Verdadeiros
A[L]⇾ Rótulos previstos da propagação para frente
O objetivo da função de perda é medir a discrepância entre os rótulos previstos e os rótulos verdadeiros. Ao minimizar essa perda, buscamos aproximar as previsões do nosso modelo o máximo possível da verdade absoluta.
Para treinar o modelo e minimizar a perda, empregamos uma técnica chamada propagação para trás (retropropagação). Esta técnica calcula os gradientes da função de custo em relação aos pesos e vieses, indicando a direção e magnitude dos ajustes necessários para cada parâmetro.
Depois de calcular os gradientes, podemos ajustar os pesos e vieses para minimizar a perda. As seguintes equações são usadas para atualizar os parâmetros usando uma taxa de aprendizado alpha:
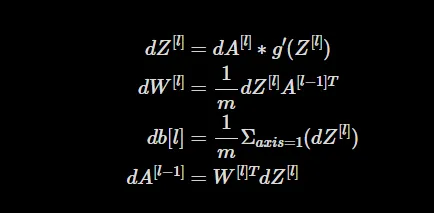
Derivações dessas equações podem ser encontradas aqui.
Essas equações atualizam os pesos e vieses de cada camada com base em seus respectivos gradientes. Ao realizar iterativamente as passagens para frente e para trás, e atualizando os parâmetros usando os gradientes, permitimos que o modelo aprenda e melhore seu desempenho ao longo do tempo.
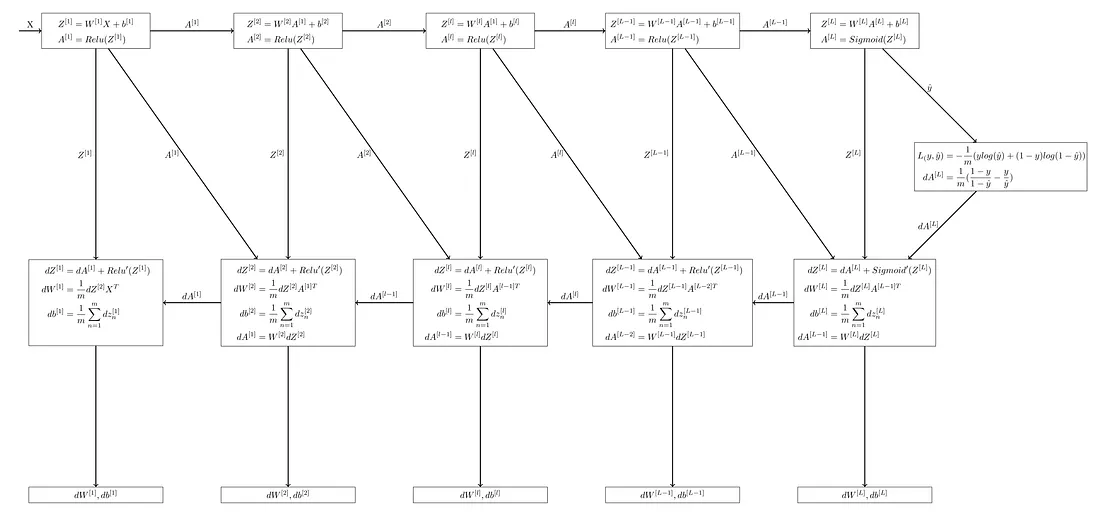
O repositório git para todo o código até esta parte é fornecido no link abaixo. Por favor, consulte-o caso esteja com alguma dificuldade.
Função de Custo
Para calcular a função de custo com base na equação de custo acima, precisamos primeiro fornecer um trait de logaritmo para o Array2<f32>, já que não podemos obter o logaritmo de um array em rust diretamente. Faremos isso escrevendo o seguinte código no início de lib.rs.
trait Log {
fn log(&self) -> Array2<f32>;
}
impl Log for Array2<f32> {
fn log(&self) -> Array2<f32> {
self.mapv(|x| x.log(std::f32::consts::E))
}
}
Em seguida, no nosso impl DeepNeuralNetwork, adicionaremos uma função para calcular o custo.
pub fn cost(&self, al: &Array2<f32>, y: &Array2<f32>) -> f32 {
let m = y.shape()[1] as f32;
let cost = -(1.0 / m)
* (y.dot(&al.clone().reversed_axes().log())
+ (1.0 - y).dot(&(1.0 - al).reversed_axes().log()));
return cost.sum();
}
Aqui passamos as ativações da última camada al e os rótulos verdadeiros y para calcular o custo.
Ativações para Trás
pub fn sigmoid_prime(z: &f32) -> f32 {
sigmoid(z) * (1.0 - sigmoid(z))
}
pub fn relu_prime(z: &f32) -> f32 {
match *z > 0.0 {
true => 1.0,
false => 0.0,
}
}
pub fn sigmoid_backward(da: &Array2<f32>, activation_cache: ActivationCache) -> Array2<f32> {
da * activation_cache.z.mapv(|x| sigmoid_prime(&x))
}
pub fn relu_backward(da: &Array2<f32>, activation_cache: ActivationCache) -> Array2<f32> {
da * activation_cache.z.mapv(|x| relu_prime(&x))
}
A função sigmoid_prime calcula a derivada da função de ativação sigmoide. Ela recebe a entrada z e retorna o valor da derivada, que é computado como o sigmoide de z multiplicado por 1.0 menos o sigmoide de z.
A função relu_prime calcula a derivada da função de ativação ReLU. Ela recebe a entrada z e retorna 1.0 se z for maior que 0, e 0.0 caso contrário.
A função sigmoid_backward calcula a propagação para trás para a função de ativação sigmoide. Ela pega a derivada da função de custo em relação à ativação da e o cache de ativação activation_cache. Realiza uma multiplicação elemento a elemento entre da e a derivada da função sigmoide, aplicada aos valores no cache de ativação activation_cache.z.
A função relu_backward calcula a propagação para trás para a função de ativação ReLU. Ela recebe a derivada da função de custo com relação à ativação da e o cache de ativação activation_cache. Ela realiza uma multiplicação elemento a elemento entre da e a derivada da função ReLU, aplicada aos valores no cache de ativação activation_cache.z.
Propagação Linear para Trás
pub fn linear_backward(
dz: &Array2<f32>,
linear_cache: LinearCache,
) -> (Array2<f32>, Array2<f32>, Array2<f32>) {
let (a_prev, w, _b) = (linear_cache.a, linear_cache.w, linear_cache.b);
let m = a_prev.shape()[1] as f32;
let dw = (1.0 / m) * (dz.dot(&a_prev.reversed_axes()));
let db_vec = ((1.0 / m) * dz.sum_axis(Axis(1))).to_vec();
let db = Array2::from_shape_vec((db_vec.len(), 1), db_vec).unwrap();
let da_prev = w.reversed_axes().dot(dz);
(da_prev, dw, db)
}
A função linear_backward calcula a propagação para trás para o componente linear de uma camada. Ela recebe o gradiente da função de custo em relação à saída linear dz e o cache linear linear_cache. Ela retorna os gradientes em relação à ativação da camada anterior da_prev, os pesos dw e os vieses db.
A função primeiro extrai a ativação da camada anterior a_prev, a matriz de pesos w e a matriz de vieses _b do cache linear. Ela calcula o número de exemplos de treinamento m acessando a forma de a_prev e dividindo o número de exemplos por m.
A função então calcula o gradiente dos pesos dw usando o produto escalar entre dz e a a_prev transposta, escalado por 1/m. Calcula o gradiente dos vieses db somando os elementos de dz ao longo do Axis(1) e escalando o resultado por 1/m. Finalmente, calcula o gradiente da ativação da camada anterior da_prev, fazendo o produto escalar entre o w transposto e o dz.
A função retorna da_prev, dw e db.
Propagação para Trás
impl DeepNeuralNetwork {
pub fn initialize_parameters(&self) -> HashMap<String, Array2<f32>> {
// o mesmo da última parte
}
pub fn forward(
&self,
x: &Array2<f32>,
parameters: &HashMap<String, Array2<f32>>,
) -> (Array2<f32>, HashMap<String, (LinearCache, ActivationCache)>) {
// o mesmo da última parte
}
pub fn backward(
&self,
al: &Array2<f32>,
y: &Array2<f32>,
caches: HashMap<String, (LinearCache, ActivationCache)>,
) -> HashMap<String, Array2<f32>> {
let mut grads = HashMap::new();
let num_of_layers = self.layers.len() - 1;
let dal = -(y / al - (1.0 - y) / (1.0 - al));
let current_cache = caches[&num_of_layers.to_string()].clone();
let (mut da_prev, mut dw, mut db) =
linear_backward_activation(&dal, current_cache, "sigmoid");
let weight_string = ["dW", &num_of_layers.to_string()].join("").to_string();
let bias_string = ["db", &num_of_layers.to_string()].join("").to_string();
let activation_string = ["dA", &num_of_layers.to_string()].join("").to_string();
grads.insert(weight_string, dw);
grads.insert(bias_string, db);
grads.insert(activation_string, da_prev.clone());
for l in (1..num_of_layers).rev() {
let current_cache = caches[&l.to_string()].clone();
(da_prev, dw, db) =
linear_backward_activation(&da_prev, current_cache, "relu");
let weight_string = ["dW", &l.to_string()].join("").to_string();
let bias_string = ["db", &l.to_string()].join("").to_string();
let activation_string = ["dA", &l.to_string()].join("").to_string();
grads.insert(weight_string, dw);
grads.insert(bias_string, db);
grads.insert(activation_string, da_prev.clone());
}
grads
}
O método backward na struct DeepNeuralNetwork executa o algoritmo de propagação para trás para calcular os gradientes da função de custo em relação aos parâmetros (pesos e vieses) de cada camada.
O método recebe a ativação final al obtida da propagação para frente, os rótulos verdadeiros y e os caches contendo os valores lineares e de ativação para cada camada.
Primeiro, o método inicializa um HashMap vazio chamado grads para armazenar os gradientes. Calcula a derivada inicial da função de custo em relação à al usando a fórmula fornecida.
Depois, começando da última camada (camada de saída), recupera o cache para a camada atual e chama a função linear_backward_activation para calcular os gradientes da função de custo em relação aos parâmetros dessa camada. A função de ativação usada é “sigmoide” para a última camada. Os gradientes computados para os pesos, vieses e ativação são armazenados no hashmap grads.
Em seguida, o método itera sobre as camadas restantes em ordem reversa. Para cada camada, ele recupera o cache, chama a função linear_backward_activation para calcular os gradientes e os armazena no hashmap grads.
Finalmente, o método retorna o hashmap grads contendo os gradientes da função de custo em relação a cada parâmetro da rede neural.
Isso completa a etapa de propagação para trás, onde os gradientes da função de custo são computados em relação aos pesos, vieses e ativações de cada camada. Esses gradientes serão usados na etapa de otimização para atualizar os parâmetros e minimizar o custo.
Atualizar Parâmetros
pub fn update_parameters(
&self,
params: &HashMap<String, Array2<f32>>,
grads: HashMap<String, Array2<f32>>,
m: f32,
learning_rate: f32,
) -> HashMap<String, Array2<f32>> {
let mut parameters = params.clone();
let num_of_layers = self.layer_dims.len() - 1;
for l in 1..num_of_layers + 1 {
let weight_string_grad = ["dW", &l.to_string()].join("").to_string();
let bias_string_grad = ["db", &l.to_string()].join("").to_string();
let weight_string = ["W", &l.to_string()].join("").to_string();
let bias_string = ["b", &l.to_string()].join("").to_string();
*parameters.get_mut(&weight_string).unwrap() = parameters[&weight_string].clone()
- (learning_rate * (grads[&weight_string_grad].clone() + (self.lambda/m) *parameters[&weight_string].clone()) );
*parameters.get_mut(&bias_string).unwrap() = parameters[&bias_string].clone()
- (learning_rate * grads[&bias_string_grad].clone());
}
parameters
}
Agora vamos atualizar os parâmetros usando os gradientes que calculamos.
Neste código, passamos por cada camada e atualizamos os parâmetros no HashMap para cada camada usando o HashMap de gradientes naquela camada. Isso nos retornará os parâmetros atualizados.
Isso é tudo para esta parte. Eu sei que isso foi um pouco complicado, mas esta parte é o coração de uma rede neural profunda. Aqui estão alguns recursos que podem ajudá-lo a entender o algoritmo de forma mais visual.
Uma Visão Geral do Algoritmo de Propagação para Trás: https://www.youtube.com/watch?v=Ilg3gGewQ5U&t=203s
Cálculo Por Trás do Algoritmo de Propagação para Trás: https://www.youtube.com/watch?v=tIeHLnjs5U8
Na próxima e última parte desta série, vamos executar nosso loop de treinamento e testar nosso modelo em algumas imagens de gatos 🐈.
Repositório GitHub: https://github.com/akshayballal95/dnn_rust_blog.git
Quer se conectar?
Artigo original publicado por Akshay Ballal. Traduzido por Paulinho Giovannini.

