Rede Neural Profunda do Zero em Rust 🦀 - Parte 3 - Propagação para Frente

Série sobre Rede Neural Profunda do Zero em Rust

No post anterior da nossa série do blog, discutimos como inicializar um modelo de rede neural (NN) com camadas especificadas e unidades ocultas. Agora, nesta parte, exploraremos o algoritmo de propagação para frente (propagação direta), uma etapa fundamental no processo de previsão da NN.

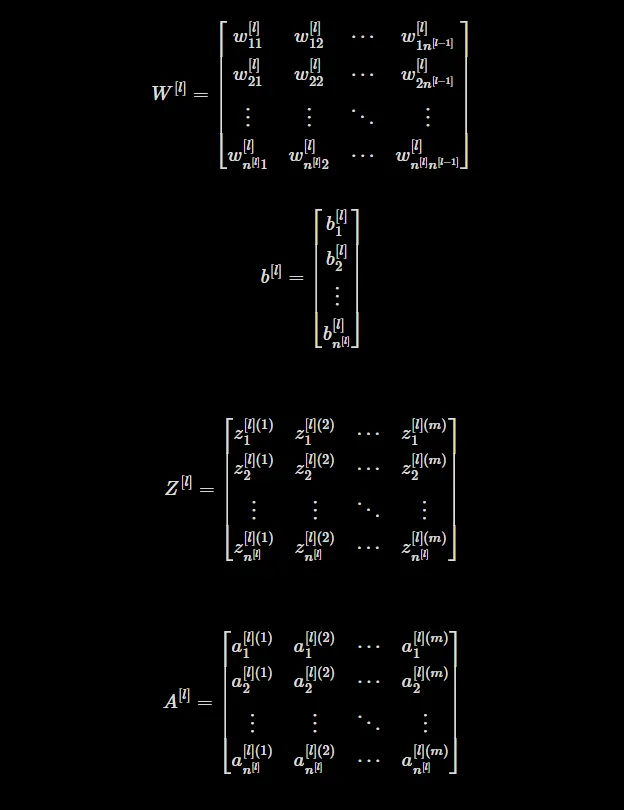
Antes de mergulharmos no aspecto de codificação, vamos entender os conceitos matemáticos subjacentes à propagação para frente. Usaremos as seguintes notações:

• Z^[l]: Matriz de logits para a camada l. Ela representa a transformação linear das entradas para uma camada específica.
• A^[l]: Matriz de ativação para a camada l. Ela representa os valores de saída ou ativação dos neurônios em uma camada específica.
• W^[l]: Matriz de pesos para a camada l. Ela contém os pesos que conectam os neurônios da camada l-1 aos neurônios da camada l.
• b^[l]: Matriz de viés para a camada l. Ela contém os valores de viés adicionados à transformação linear das entradas para a camada l.

Além disso, temos a matriz de entrada denotada como X, que é igual à matriz de ativação A^[0] da camada de entrada.

Para realizar a propagação para frente, precisamos seguir estas duas etapas para cada camada:

1. Calcule a matriz de logits para cada camada usando a seguinte expressão:

Z^[l] = W^[l]A^[l-1] + b^[l]

Em termos mais simples, a matriz de logits para a camada l é obtida pegando o produto escalar da matriz de peso W^[l] e a matriz de ativação A^[l-1] da camada anterior, e então somando a matriz de viés b^[l]. Esta etapa representa a transformação linear das entradas para a camada atual.

1. Calcule a matriz de ativação a partir da matriz de logits usando uma função de ativação:

A^[l]= FunçãoDeAtivação(Z^[l])

Aqui, a função de ativação pode ser qualquer função não linear aplicada elemento a elemento aos elementos da matriz de logits. Funções de ativação populares incluem sigmoid, tanh e relu. Em nosso modelo, usaremos a função de ativação relu para todas as camadas intermediárias e sigmoid para a última camada (camada classificadora). Esta etapa introduz não linearidade na rede, permitindo que ela aprenda e modele relações complexas nos dados.

Para n^[l] número de unidades ocultas na camada l e m número de exemplos, essas são as formas de cada matriz:

Z[l] ⇾ [n[l] x m]

W[l] ⇾ [n[l] x n[l-1]]

b[l] ⇾ [n[l] x 1]

A[l] ⇾ [n[l] x m]

Durante o processo de propagação para frente, armazenaremos a matriz de peso, a matriz de viés e a matriz de logits como cache. Essas informações armazenadas serão úteis na etapa subsequente de propagação para trás (retropropagação), onde atualizamos os parâmetros do modelo com base nos gradientes calculados.

Ao realizar a propagação para frente, nossa rede neural leva os dados de entrada por todas as camadas, aplicando transformações lineares e funções de ativação, e eventualmente produz uma previsão ou saída na camada final.

Dependências

Adicione esta linha ao arquivo Cargo.toml.

num-integer = "0.1.45" 

Structs de Cache

Primeiro, no arquivo lib.rs definiremos duas structs - LinearCache e ActivationCache

//lib.rs

use num_integer::Roots;

#[derive(Clone, Debug)]
pub struct LinearCache {
    pub a: Array2<f32>,
    pub w: Array2<f32>,
    pub b: Array2<f32>,
}

#[derive(Clone, Debug)]
pub struct ActivationCache {
    pub z: Array2<f32>,
}

A struct LinearCache armazena os valores intermediários necessários para cada camada. Ela inclui a matriz de ativação (activation) a, a matriz de peso (weight) w, e a matriz de viés (bias) b. Essas matrizes são usadas para calcular a matriz de logits z no processo de propagação para frente.

A struct ActivationCache armazena a matriz de logits z para cada camada. Este cache é essencial para etapas posteriores, como a propagação para trás, onde os valores armazenados são necessários.

Definir Funções de Ativação

Em seguida, vamos definir as funções de ativação não-lineares que iremos utilizar - relu e sigmoid

//lib.rs

pub fn sigmoid(z: &f32) -> f32 {
    1.0 / (1.0 + E.powf(-z))
}

pub fn relu(z: &f32) -> f32 {
    match *z > 0.0 {
        true => *z,
        false => 0.0,
    }
}

pub fn sigmoid_activation(z: Array2<f32>) -> (Array2<f32>, ActivationCache) {
    (z.mapv(|x| sigmoid(&x)), ActivationCache { z })
}

pub fn relu_activation(z: Array2<f32>) -> (Array2<f32>, ActivationCache) {
    (z.mapv(|x| relu(&x)), ActivationCache { z })
}

As funções de ativação introduzem não linearidade às redes neurais e desempenham um papel crucial no processo de propagação para frente. O código fornece implementações para duas funções de ativação comumente usadas: sigmoid e relu.

A função sigmoid recebe um único valor z como entrada e retorna a ativação sigmoide, que é calculada usando a fórmula sigmoide: 1 / (1 + e^-z). A função sigmoid mapeia o valor de entrada para um intervalo entre 0 e 1, permitindo que a rede modele relações não-lineares.

A função relu recebe um único valor z como entrada e aplica a ativação de Unidade Linear Retificada (ReLU). Se z for maior que zero, a função retorna z; caso contrário, retorna zero. ReLU é uma função de ativação popular que introduz não linearidade e ajuda a rede a aprender padrões complexos.

Tanto as funções sigmoid quanto relu são usadas para valores individuais ou como blocos de construção para as funções de ativação baseadas em matriz.

O código também fornece duas funções de ativação baseadas em matriz: sigmoid_activation e relu_activation. Estas funções recebem uma matriz 2D z como entrada e aplicam a respectiva função de ativação elemento a elemento usando a função mapv. A matriz de ativação resultante é retornada juntamente com uma struct ActivationCache, que armazena a matriz de logits correspondente.

Propagação Linear para Frente

//lib.rs

pub fn linear_forward(
    a: &Array2<f32>,
    w: &Array2<f32>,
    b: &Array2<f32>,
) -> (Array2<f32>, LinearCache) {
    let z = w.dot(a) + b;

    let cache = LinearCache {
        a: a.clone(),
        w: w.clone(),
        b: b.clone(),
    };
    return (z, cache);
}

A função linear_forward recebe a matriz de ativação a, a matriz de peso w e a matriz de bias b como entradas. Ela realiza a transformação linear calculando o produto escalar de w e a, e então adiciona b ao resultado. A matriz resultante z representa os logits da camada. A função retorna z juntamente com uma struct LinearCache, que armazena as matrizes de entrada para uso posterior na propagação para trás.

Propagação Linear Ativada para Frente

//lib.rs

pub fn linear_forward_activation(
    a: &Array2<f32>,
    w: &Array2<f32>,
    b: &Array2<f32>,
    activation: &str,
) -> Result<(Array2<f32>, (LinearCache, ActivationCache)), String> {
    match activation {
        "sigmoid" => {
            let (z, linear_cache) = linear_forward(a, w, b);
            let (a_next, activation_cache) = sigmoid_activation(z)?;
            return Ok((a_next, (linear_cache, activation_cache)));
        }
        "relu" => {
            let (z, linear_cache) = linear_forward(a, w, b);
            let (a_next, activation_cache) = relu_activation(z)?;
            return Ok((a_next, (linear_cache, activation_cache)));
        }
        _ => return Err("string de ativação incorreta".to_string()),
    }
}

A função linear_forward_activation se baseia na função linear_forward. Ela recebe as mesmas matrizes de entrada que linear_forward, juntamente com um parâmetro adicional activation, indicando a função de ativação a ser aplicada. A função primeiro chama linear_forward para obter os logits z e o cache linear. Então, dependendo da função de ativação especificada, ela chama sigmoid_activation ou relu_activation para calcular a matriz de ativação a_next e o cache de ativação. A função retorna a_next junto com uma tupla do cache linear e do cache de ativação, envolvida em um enum Result. Se a função de ativação especificada não for suportada, uma mensagem de erro é retornada.

Propagação para Frente

impl DeepNeuralNetwork {
    /// Inicializa os parâmetros da rede neural.
    ///
    /// ### Retorna
    /// Um dicionário Hashmap com pesos e vieses inicializados aleatoriamente.
    pub fn initialize_parameters(&self) -> HashMap<String, Array2<f32>> {
        // mesmo que a parte anterior
    }

    pub fn forward(
        &self,
        x: &Array2<f32>,
        parameters: &HashMap<String, Array2<f32>>,
    ) -> (Array2<f32>, HashMap<String, (LinearCache, ActivationCache)>) {
        let number_of_layers = self.layers.len() - 1;

        let mut a = x.clone();
        let mut caches = HashMap::new();

        for l in 1..number_of_layers {
            let w_string = format!("W{}", l);
            let b_string = format!("b{}", l);

            let w = &parameters[&w_string];
            let b = &parameters[&b_string];

            let (a_temp, cache_temp) = linear_forward_activation(&a, w, b, "relu").unwrap();

            a = a_temp;

            caches.insert(l.to_string(), cache_temp);
        }

        // Calcula a ativação da última camada com a função sigmoid
        let weight_string = format!("W{}", number_of_layers);
        let bias_string = format!("b{}", number_of_layers);

        let w = &parameters[&weight_string];
        let b = &parameters[&bias_string];

        let (al, cache) = linear_forward_activation(&a, w, b, "sigmoid").unwrap();
        caches.insert(number_of_layers.to_string(), cache);

        return (al, caches);
    }
}

O método forward na implementação DeepNeuralNetwork realiza o processo de propagação para frente para toda a rede neural. Ele recebe a matriz de entrada x e os parâmetros (pesos e vieses) como entradas. O método inicializa a matriz a como uma cópia de x e cria um hashmap vazio chamado caches para armazenar os caches de cada camada.

Em seguida, ele itera sobre cada camada (exceto a última) em um loop for. Para cada camada, ele recupera os pesos w correspondentes e os vieses b dos parâmetros usando concatenação de strings. Em seguida, chama linear_forward_activation com a, w, b e a função de ativação definida como "relu". A matriz de ativação resultante a_temp e o cache cache_temp são armazenados no hashmap caches usando o índice da camada como chave. A matriz a é atualizada para a_temp para a próxima iteração.

Depois de processar todas as camadas intermediárias, a ativação da última camada é calculada usando a função de ativação sigmoid. Ela recupera para a última camada os pesos w e os vieses b dos parâmetros e chama linear_forward_activation com a, w, b e a função de ativação definida como sigmoide. A matriz de ativação resultante al e o cache são armazenados no hashmap caches usando o índice da última camada como chave.

Finalmente, o método retorna a matriz de ativação final al e o hashmap caches contendo todos os caches de cada camada. Aqui al é a ativação da camada final e será usada para fazer as previsões durante a parte de inferência do nosso processo.

Isso é tudo sobre a Propagação para Frente

Em conclusão, abordamos um aspecto importante da construção de uma rede neural profunda neste post de blog: a propagação para frente. Aprendemos como os dados de entrada se movem pelas camadas, passam por transformações lineares e são ativados usando diferentes funções.

Mas nossa jornada não termina aqui! No próximo post do blog, mergulharemos em tópicos empolgantes como a função de perda e a propagação para trás. Exploraremos como medir o erro entre as previsões e as saídas reais, e como usar esse erro para atualizar nosso modelo. Essas etapas são cruciais para treinar a rede neural e melhorar seu desempenho.

Portanto, fique atento ao próximo post do blog, onde vamos entender e implementar uma função de perda de entropia cruzada binária e realizaremos a propagação para trás.

Quer se conectar?

Meu website
LinkedIn
Twitter

Artigo original publicado por Akshay Ballal. Traduzido por Paulinho Giovannini.